Nos nove ensaios sobre o universo [veja o painel à esquerda], tentei estabelecer um modelo alternativo para a luz como uma inscrição gravada pela fonte em um fluxo etérico que converge continuamente para o observador na velocidade c. Isso exige que a velocidade da luz c seja vinculada exclusivamente ao referencial do observador. Portanto, agora discuto a passagem da luz, de uma fonte para um observador, do ponto de vista do quadro de referência do observador.
Devemos ter muito cuidado para não pensar subconscientemente no pedaço de papel ou na janela do navegador, sobre ou dentro do qual o diagrama a seguir aparece, como um quadro de referência. É fácil olhar para o diagrama e pensar na posição do fantasma — isto é: o lugar onde o observado estava quando emitiu a luz — como "estacionário".
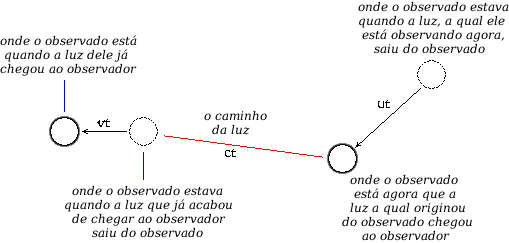
Mas "estacionário" relativo ao que? Toda a página (ou janela do navegador) pode estar "em movimento". Podemos evitar esse problema de velocidade relativa da seguinte maneira. Considere o instante em que um fóton de luz está emitido pelo observado. Este "instante" ocupa uma período de tempo infinitésimalmente pequeno δt. Consequentemente, todo o movimento no universo está efetivamente "congelado" durante este período. Neste momento, o observado ocupa uma posição definitiva no espaço e no tempo.
O tempo então continua e o fóton afasta-se do seu ponto de partida. No que diz respeito ao fóton, o movimento futuro do observado é irrelevante. Não desempenha mais nenhum papel significativo na determinação do caminho ou destino do fóton. Durante a viagem do fóton, o observador — o destino final do fóton — também é irrelevante. Nem o observado nem o observador influenciam ou afetam a viagem do fóton de forma significativa. Eventualmente, durante um outro período infinitamente pequeno de duração δt, o fóton atinge um átomo no olho do observador, contribuindo para a visão geral do observado como experimentado pelo observador.
Se o observador está ou não em movimento em relação ao ponto de origem do fóton é irrelevante. Isso não afeta o fato de que quando o fóton é absorvido, percorreu uma distância definida e tomou um tempo definido para fazê-lo. Dividir esta distância definitiva por este tempo definido produz uma constante natural chamada a velocidade da luz. No entanto, esta "velocidade" não se aplica apenas à luz. É também a "velocidade máxima" na qual todas as influências podem ser transmitidas de um lugar para outro. É a "velocidade máxima" na qual a informação pode ser propagada.
A conseqüência fundamental dessa "velocidade" máxima para a transferência de informações é que um observador só pode ver — e só pode ser afetado por — eventos passados. Por outro lado, um observado só pode ser visto por — e só pode ter um efeito sobre — um observador no futuro. O que alguém faz "agora" somente pode afetar os outros "mais tarde". Isto não é apenas uma limitação da escala humana e do físico: é uma limitação fundamental incorporada ao próprio tecido da existência. Isso leva a uma consequência adicional.
A realidade, dentro da qual existe qualquer observador específico, só pode possivelmente ser uma pequena parte do totalidade do que existe. A sua realidade compreende apenas a parte de toda a realidade que se encontra dentro de uma esfera "sólida" do espaço-tempo o que é exclusivamente dele, no centro do qual ele reside. O raio desta esfera estende-se longe da posição atual do observador no espaço e para trás da posição atual dele no tempo.
Os pontos equidistantes do observador em direções diferentes podem ser separados por grandes distâncias. E, embora equidistantes para dentro do passado dele, esses pontos equidistantes podem ocupar posições muito diferentes no tempo em relação umas com as outras. Ir para trás para dentro do passado em uma direção não é a mesma coisa que ir para trás para dentro do passado em outra direção. Assim, o próprio tempo, como distância, deve necessariamente ser também uma quantidade vetorial. Do ponto de vista do observador, portanto, apenas as distâncias radiais diretas, dentro da esfera de observação dele, são relevantes ou reais.
O observador pode, em qualquer instante, ver — ou de outra forma ser afetado de forma independente por — eventos dentro desta esfera. É o único e exclusivo universo observável dele. É a única e exclusiva realidade dele. Mas é um universo, ou realidade, o qual o observador si mesmo é fundamentalmente incapaz de influenciar ou mudar. Ele não pode mudar ou influenciar a história que ele pode ver e experimentar.
Se o nosso observador agir de maneira que resulte em sua luz emissora ou alguma outra influência, então essa luz ou influência viaja para fora dele para outra esfera do espaço-tempo — para um outro universo — sobre o qual ele não sabe nada. Ele não pode mudar a sua própria história, mas ele pode influenciar a futura "história" dos outros.
Um Experimento de Pensamento Alternativo
Considere uma nave espacial que compreende 3 módulos iguais. Cada módulo é cilíndrico. Os 3 módulos são conectados em linha para formar um cilindro 3 vezes o comprimento de cada módulo individual. Os módulos são conectados em conjunto por mecanismo de lançamento rápido.

Entre cada par de módulos existe uma mola forte comprimida. Os mecanismos que atam os módulos em conjunto são lançados simultaneamente. As molas aceleram os dois módulos exteriores em direções opostas, longe do módulo central, em uma linha direta. Isto ocorre para que os módulos exteriores viagem para longe do módulo central em uma fração relativisticamente significante da velocidade da luz, v. Eles continuam a sua viagem em direções opostas indefinidamente.

Cada módulo espacial tem a bordo um relógio preciso. Enquanto os 3 módulos ainda estavam conectados, em outras palavras, antes que os mecanismos de lançamento rápido operassem, os relógios nos 3 módulos foram sincronizados. Eles mostravam exatamente a mesma hora.
Vamos considerar a hora mostrado no relógio de bordo de um dos módulos que "viajaram" comparado com o relógio de bordo do módulo central "estacionário". O módulo que viajou esteve viajando por bastante tempo. Suponhamos que o tempo decorrido mostrado no relógio do módulo "estacionário" é T.
Se o efeito de dilação de tempo da relatividade for verdadeiramente deformando o "tecido" do espaço-tempo, então o tempo decorrido indicado pelo relógio no módulo "em movimento" seria menos do que T. Contudo, para a pessoa a bordo do módulo "em movimento", o tempo parece passar normalmente. Se isto for verdadeiro, o seu relógio deve indicar a mesmo tempo decorrido, ou seja, T. Vamos supor que ambos os relógios indicam um tempo decorrido de T. A pergunta é: o que a tripulação do módulo "estacionário" percebe quanto a hora indicada pelo relógio do módulo "em movimento"?
Para este exercício, tomaremos a liberdade de fazer a suposição de que a informação não pode viajar mais rápido do que a velocidade da luz. Se esta suposição for alguma vez comprovada estar incorreta, então, o nosso argumento é falho. Contudo, assumindo que isto seja verdadeira, a tripulação do módulo "estacionário" nunca poderá observar a posição real do módulo "em movimento". Nem eles poderão observar alguma vez o tempo real mostrado no relógio do módulo "em movimento". Eles só podem sempre ver, perceber ou por qualquer meio obter informação sobre um "fantasma" passado do módulo "em movimento" e o seu relógio.
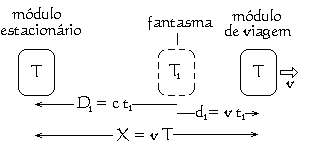
Este fantasma passado é o módulo "em movimento" como era no montante de tempo t1 no passado. Aqui, t1 é o tempo que a informação leva para viajar a distância D1 da posição do fantasma ao módulo "estacionário". Desde que a velocidade máxima, na qual a informação pode viajar, é aquela da luz c, esta distância deve ser dada por D1 = c t1. O tempo passado T1, mostrado no relógio do fantasma no tempo passado T no relógio do módulo "estacionário", deve ser dado por T1 = T − t1.
Como o módulo "em movimento" move-se além disso e mais ao longe do módulo "estacionário", o tempo t1 requerido para a informação chegar ao observador no módulo "estacionário" aumentará continuamente. Conseqüentemente, como t1 aumenta, T − t1 reduz. Daqui, o relógio de bordo no fantasma — o que o observador no módulo "estacionário" percebe como sendo o módulo "em movimento" — parece estar correndo lentamente. Os segundos neste relógio remoto são mais longos do que aqueles do relógio local. Além disso, o fantasma cai mais e mais para trás do módulo real, assim continuamente aumentando a distância entre eles.

Vamos agora considerar a distância D1 do fantasma em relação ao observador, em termos da distância X da realidade para o observador. A intuição sugeriria que, enquanto a realidade viaja mais e mais distante do observador, o fantasma mais e mais retarda-se atrás da realidade. A álgebra adjacente consegue uma expressão formal de D1 em termos de X. Isto mostra que se a velocidade v do módulo "em movimento" for uma constante, então a distância D1 será uma fração constante de X. Se o módulo "em movimento" viajasse na velocidade da luz, o seu fantasma viajaria na metade da velocidade da luz. Se o módulo "em movimento" viajasse em um milhão de vezes a velocidade da luz, o seu fantasma viajaria em só 1000000 ÷ 1000001 vezes a velocidade da luz, que é igual 0,9999990000c. Conseqüentamente, em a qualquer velocidade a realidade viaja relativamente ao observador, o observador a verá somente como um fantasma que viaja menos que a velocidade da luz.
Naturalmente, a álgebra é um pouco mais complicada para um observador que está localizado fora da linha da trajetória do módulo "em movimento". Contudo, o princípio essencial é o mesmo.
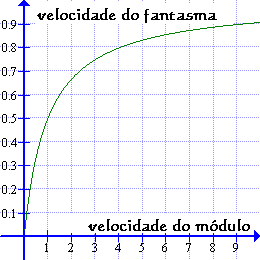 A proporção entre a distância X (do módulo "em movimento") e a distância D (do seu fantasma) para o módulo "estacionário" varia inversamente à velocidade v do módulo "em movimento". As velocidade deles também deve estar nesta mesma proporção. O gráfico à esquerda usa esta proporção para traçar a velocidade do fantasma contra a velocidade do módulo "em movimento" em unidades de c, a velocidade da luz. Ignore somente, por enquanto, a "legalidade" física do módulo que viaja além da velocidade da luz. Vemos que, no entanto rápido o módulo viaja, o seu fantasma — que é para o observador a realidade física eficaz do módulo — nunca pode alcançar a velocidade da luz.
A proporção entre a distância X (do módulo "em movimento") e a distância D (do seu fantasma) para o módulo "estacionário" varia inversamente à velocidade v do módulo "em movimento". As velocidade deles também deve estar nesta mesma proporção. O gráfico à esquerda usa esta proporção para traçar a velocidade do fantasma contra a velocidade do módulo "em movimento" em unidades de c, a velocidade da luz. Ignore somente, por enquanto, a "legalidade" física do módulo que viaja além da velocidade da luz. Vemos que, no entanto rápido o módulo viaja, o seu fantasma — que é para o observador a realidade física eficaz do módulo — nunca pode alcançar a velocidade da luz.

Agora podemos derivar o tempo mostrado pelo relógio de bordo do módulo "em movimento" do ponto da visão do observador a bordo do módulo "estacionário"....
Para o observador a bordo do módulo "estacionário", o fantasma do módulo "em movimento" não é uma ilusão. Ele é a coisa real em todos os sentidos. Ele não é somente a posição de onde a imagem visível do módulo "em movimento" origina-se. Ele é também o lugar de onde a sua influência gravitacional origina-se. Ele é o lugar de origem de todos os efeitos físicos do módulo "em movimento" sobre o módulo "estacionário". Ele é a única conexão do módulo "em movimento" com a quadro de referência do módulo "estacionário". A realidade do próprio módulo "em movimento" está efetivamente fora do universo do módulo "estacionário".
O movimento é relativo. Conseqüentemente, o qual módulo é considerado como "estacionário" e o qual módulo é considerado como "viajando" é arbitrário. Tudo depende o qual módulo atualmente consideramos para ser o "observador". "O observador" e "o observado", por isso, podem ser livremente permutados sem alterar o princípio do nosso experimento. Cada módulo, por isso, pode observar e ser afetado por somente o fantasma do outro. As respectivas realidades dos dois módulos são fundamentalmente incapazes de comunicar diretamente um com o outro. A realidade de cada um pode ser observada e afetada somente pelo fantasma do outro.
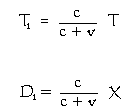 Do acima mencionado, vimos que — do ponto de vista do observador — o tempo no módulo "em movimento" dilata-se por um montante dado pela fórmula à direita.
Do acima mencionado, vimos que — do ponto de vista do observador — o tempo no módulo "em movimento" dilata-se por um montante dado pela fórmula à direita.
Também vimos que — do ponto de vista do observador — a distância entre o observador e o módulo "em movimento" contrai-se por um montante dado pela fórmula á direita.
Além disso, se, do ponto de vista do módulo estacionário, a distância ao módulo de viagem parece contrair-se, o mesmo deve ocorrer com o comprimento físico do próprio módulo de deslocamento.
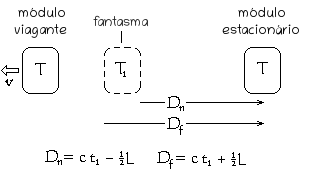 No diagrama à esquerda, Dn é a distância da extremidade próxima do objeto fantasma do olho do observador a bordo do módulo "estacionário". Correspondentemente, Df é a distância da extremidade mais distante do fantasma. Df é maior que Dn por um valor igual ao comprimento da imagem fantasma do módulo "viajante". Portanto, a luz demora um pouco mais para alcançar o olho do observador do outro extremo do módulo de "viagem" do que do seu fim próximo. Esse tempo extra é L / c, onde L é o comprimento do fantasma.
No diagrama à esquerda, Dn é a distância da extremidade próxima do objeto fantasma do olho do observador a bordo do módulo "estacionário". Correspondentemente, Df é a distância da extremidade mais distante do fantasma. Df é maior que Dn por um valor igual ao comprimento da imagem fantasma do módulo "viajante". Portanto, a luz demora um pouco mais para alcançar o olho do observador do outro extremo do módulo de "viagem" do que do seu fim próximo. Esse tempo extra é L / c, onde L é o comprimento do fantasma.
O observador vê a extremidade mais distante do fantasma e a extremidade próxima do fantasma ao mesmo tempo. A luz que ele vê chegando do outro extremo do fantasma deve, portanto, ter iniciado sua jornada até ele um pouco mais cedo do que a luz da extremidade mais próxima do fantasma. A luz do extremo oposto do fantasma deve ter deixado o fantasma quando o fantasma estava mais perto do observador do que quando a luz deixou a extremidade próxima do fantasma. Consequentemente, o fantasma parecerá ser mais curto do que realmente é.
Mas isto é uma verdadeira contração de espaço e dilação do tempo? Para responder isto, vamos considerar o terceiro módulo que viajou no sentido contrário. Este terceiro módulo tem uma velocidade em relação ao primeiro módulo "em movimento" que é o dobro da velocidade entre o módulo "estacionário" e o primeiro módulo "em movimento". A um observador a bordo do segundo módulo "em movimento", o fantasma do primeiro módulo "em movimento" estará em uma posição diferente.
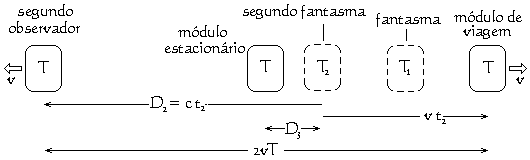
A luz do primeiro módulo "em movimento" leva mais tempo para alcançar o segundo módulo "em movimento" do que ele leva para alcançar o módulo "estacionário". O fantasma do primeiro módulo "em movimento" visto pelo observador no segundo módulo "em movimento" será, por isso, mais velho do que o fantasma do primeiro módulo "em movimento" visto pelo observador no módulo "estacionário". Do acima mencionado diagrama, conclui-se:

A distância D2 do segundo fantasma apartir do segundo módulo "em movimento" é, por isso, duas vezes a distância D1 do primeiro fantasma apartir do módulo "estacionário". A distância do segundo módulo "em movimento" do módulo "estacionário" é a mesma que a distância do primeiro módulo "em movimento" do módulo "estacionário", a saber X. A distância do segundo fantasma do módulo "estacionário" D3 é, por isso, D2 − X, conforme abaixo:

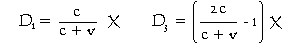 Essencialmente, D3 é diferente de D1. Isto significa que dois fantasmas separados existem e que eles ocupam posições diferentes no espaço.
Essencialmente, D3 é diferente de D1. Isto significa que dois fantasmas separados existem e que eles ocupam posições diferentes no espaço.
No diagrama seguinte coloco os módulos ligeiramente fora da linha para tornar a ilustração mais clara. Embora, estritamente falando, isto faça a geometria mais complicada, não altera os princípios que estou ilustrando.
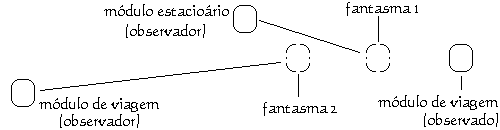
Neste diagrama podemos ver que os dois observadores estão observando duas coisas diferentes. Cada fantasma ocupa uma posição diferente no espaço. Os dois fantasmas são também diferentes na idade. O observador "em movimento" está observando um fantasma que é mais velho que o fantasma que está sendo observado pelo observador "estacionário". Conseqüentemente, os dois fantasmas estão também em posições diferentes no tempo. Os dois fantasmas são lugares de onde o real módulo "em movimento" observado já foi.
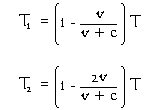 Além disso, a velocidade na qual o tempo é observado para passar é diferente para cada fantasma. O observador "estacionário" vê o tempo decorrido no relógio dentro do primeiro fantasma como T1, ao passo que o observador "em movimento" vê o tempo decorrido no relógio dentro do segundo fantasma como T2, como mostrado à direita. O observado módulo "em movimento" está movendo-se do observador "em movimento" duas vezes mais rápido que o módulo estacionário. Conseqüentemente, o relógio no segundo fantasma corre a apenas metade da velocidade do relógio no primeiro fantasma.
Além disso, a velocidade na qual o tempo é observado para passar é diferente para cada fantasma. O observador "estacionário" vê o tempo decorrido no relógio dentro do primeiro fantasma como T1, ao passo que o observador "em movimento" vê o tempo decorrido no relógio dentro do segundo fantasma como T2, como mostrado à direita. O observado módulo "em movimento" está movendo-se do observador "em movimento" duas vezes mais rápido que o módulo estacionário. Conseqüentemente, o relógio no segundo fantasma corre a apenas metade da velocidade do relógio no primeiro fantasma.
Lembre-se de que o respectivo fantasma de cada observador não é meramente o lugar de onde a imagem de luz do módulo "viajante" observado se origina. É também o lugar de onde o observador "sente" a gravitação e todas as outras influências físicas do módulo "viajante" observado. Cada observador percebe seu fantasma como a coisa real. O módulo real, para ele, não existe. Ele está além de seu horizonte de eventos.
Não obstante: na realidade verdadeira, a luz e todos os outros efeitos físicos podem, fundamentalmente, ser emitidos por — vir de — apenas o módulo real: não seu fantasma. A localização atual do fantasma é onde o módulo real estava quando emitiu a luz que o observador está recebendo agora.
Para cada observador, o tempo a bordo do módulo "em movimento" observado é dilatado a uma extensão diferente. Contudo, isto não significa que o tempo em si mesmo está de fato dilatado na proximidade do módulo "em movimento" observado. Se estivesse o caso, teria de ser dilatado em tantos quantos montantes como havia observadores que estavam observando-o. Se em vez de dois módulos observadores tivéssemos um milhão, então o tecido do tempo dentro do espaço na proximidade do módulo "em movimento" observado teria de ser dilatado por um milhão de montantes diferentes simultaneamente. Isto não soa plausível.
Uma visão muito mais plausível é que o tempo simplesmente parece ser dilatado diferentemente a cada observador. A causa desta aparente dilação, por isso, tem a ver com como a informação do módulo "em movimento" observado é transmitida a cada respetivo observador. Deve ter a ver com como o próprio espaço-tempo transmite a informação.
O Qual Sobre uma Viagem de Retorno?
Para isso, substitua nossa nave espacial de 3 módulos por uma nave espacial de 5 módulos. Cada módulo é cilíndrico. Os 5 módulos estão conectados em linha para formar um cilindro 5 vezes o comprimento de cada módulo individual. Os módulos são conectados entre si por capturas de liberação rápida.

Entre cada par de módulos adjacentes é uma mola comprimida forte. Quando a trava que liga um par de módulos adjacentes é liberada, a mola acelera os módulos separados em direções opostas em linha reta. As capturas que ligam o módulo central aos seus dois vizinhos imediatos são lançadas. As molas aceleram os dois pares de módulos ligados em direções opostas para que eles acabem viajando para longe do módulo central em quase a velocidade da luz

Observação: no experimento mental anterior de 3 módulos, as molas de cada lado do módulo central aceleraram apenas um módulo até uma fração significativa da velocidade da luz, v. Desta vez, no entanto, as molas devem ser mais fortes para conseguir acelerar dois módulos até a mesma fração significativa da velocidade da luz, v.
Eles continuam em suas jornadas em direções opostas. Depois de cada par de módulos viajar para o que a respectiva equipe percebe ser de 7 anos, cada tripulação libera a captura entre seus pares de módulos. Os dois módulos de cada par são forçados a separar-se pela mola comprimida entre eles.

A mola entre os dois módulos de cada par de saída é tão forte quanto as molas que foram liberadas 7 anos antes entre cada par de módulos e o módulo central.
Isso ocorre porque, embora cada mola precise agora acelerar apenas metade da massa, ela precisa acelerar seu par de módulos separadamente em direções opostas para atingir uma velocidade relativa entre eles de duas vezes a 'fração significativa da velocidade da luz', 2v. Isso ocorre para que o módulo de destino tenha uma velocidade relativa ao módulo estacionário da 'fração significativa da velocidade da luz' original, v.
Os dois módulos externos em cada lado do experimento continuarão em suas mesmas direções respectivas, mas agora a uma velocidade aumentada de 2v para longe do módulo central. Eles continuam a viajar separados para sempre.
Por fim, após mais 7 anos, os dois módulos que agora estão viajando de volta para o módulo central, de direções opostas, cada um a uma velocidade v em relação ao módulo central [estacionário], reconectam-se ao módulo central.

Presumivelmente, há um meio benigno de matar suas vastas velocidades relativas à medida que se encontram. Talvez algum tipo de amortecedor mecânico como antes.
As tripulações nos dois módulos externos foram submetidas a viagens simétricas. A tripulação do módulo central não foi a lugar nenhum. Consideremos agora a relação entre o módulo central "estacionário" e apenas um dos módulos "em movimento", pois está aproximando-se do "estacionário".
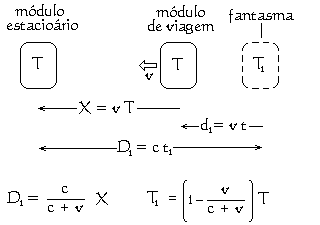 O diagrama na esquerda mostra o módulo "em movimento" aproximando-se para o módulo "estacionário" à velocidade v. Abaixo dele são as fórmulas da distância D1 do fantasma e do tempo T1 mostrado no relógio neste fantasma. Em todos os meus cenários, até agora, considero a velocidade do módulo "em movimento" v que é constante. Conseqüentemente, a expressão c ÷ (c + v) é também constante. Isto significa que a velocidade do fantasma é sempre proporcional à velocidade do módulo "em movimento".
O diagrama na esquerda mostra o módulo "em movimento" aproximando-se para o módulo "estacionário" à velocidade v. Abaixo dele são as fórmulas da distância D1 do fantasma e do tempo T1 mostrado no relógio neste fantasma. Em todos os meus cenários, até agora, considero a velocidade do módulo "em movimento" v que é constante. Conseqüentemente, a expressão c ÷ (c + v) é também constante. Isto significa que a velocidade do fantasma é sempre proporcional à velocidade do módulo "em movimento".
Essas fórmulas da viagem da volta são iguais como as fórmulas da viagem da ida. Contudo, para a viagem da volta, a velocidade v é, por convenção, negativa.

Na viagem da ida, como a velocidade do módulo é aumentada linearmente, a velocidade do seu fantasma aumenta somente logaritimamente. Mesmo que a velocidade do fantasma aumente com a velocidade do módulo, os atrasos do fantasma aumentam cada vez mais em relação à realidade do módulo "em movimento". Na viagem da volta, contudo, a velocidade do fantasma aumenta exponencialmente com o aumento linear da velocidade do módulo. Deste modo, na viagem de volta, o fantasma parece viajar em alta velocidade. Assim, há uma enorme assimetria entre a velocidade do fantasma na viagem da ida e a velocidade do fantasma na viagem da volta.
O Paradoxo Trigêmeos
Suponha que os 3 módulos do meio da nave espacial de 5 módulos contenham 1 de 3 trigêmeos. Um dos trigêmeos está no módulo do meio que, durante todo o experimento de 14 anos, não vai a lugar nenhum. Os outros dois trigêmeos viajam para fora em direções opostas por 7 anos e depois passam 7 anos retornando para seu irmão no módulo do meio. Eles têm todos a mesma idade quando retornam? Ou o tempo para os trigêmeos viajantes se dilatou, deixando-os mais jovens do que seu irmão "parado"?
Enquanto eles estão viajando em relação um ao outro em uma proporção significativa da velocidade da luz, a realidade de cada um dos trigêmeos está fora dos horizontes de eventos de seus dois irmãos. Cada um está, na verdade, totalmente desconectado de seus irmãos. Cada um está, portanto, na verdade, em um universo diferente. Os únicos aspectos de seus irmãos, que estão dentro do horizonte de eventos de qualquer um dos trigêmeos, são seus fantasmas relativísticos.
Do ponto de vista do tripleto "estacionário", os relógios fantasmas de seus dois irmãos parecem estar funcionando em uma velocidade diferente do seu relógio. Os relógios deles parecem estar funcionando mais devagar quando se afastam e mais rápido quando se aproximam. Do ponto de vista de qualquer um dos tripletos "viajantes", o relógio dentro do fantasma de seu irmão "estacionário" parecerá estar funcionando menos "mais rápido" ou "mais devagar" do que o relógio dentro do fantasma de seu irmão "viajante".
As jornadas dos dois tripletos viajantes são idênticas, exceto que eles viajaram em direções opostas. Não há evidências para supor que a taxa na qual o tempo passa seja diferente em uma direção do que em outra. Consequentemente, não importa como o relógio dentro do fantasma do módulo de um tripleto viajante pareceu se comportar do ponto de vista do outro tripleto viajante durante a jornada, o tempo para cada um deve ser o mesmo quando eles se reunirem. Ambos devem ter envelhecido na mesma quantidade, ou seja, 14 anos.
No início de sua jornada, cada um dos dois trigêmeos viajantes foi acelerado a uma grande proporção da velocidade da luz. Suas respectivas acelerações estavam em direções opostas. Mas não há razão física para que o efeito temporal da aceleração em um corpo deva ser diferente em direções diferentes. Consequentemente, uma vez que eles aceleraram na mesma quantidade, qualquer efeito temporal resultante, sofrido pelos dois trigêmeos viajantes, deve ter sido o mesmo. Suas acelerações não devem, portanto, produzir uma dilatação de tempo duradoura entre eles.
Durante suas jornadas, cada trigêmeo viajante observa seu irmão como um fantasma para quem o tempo passa mais devagar ao recuar e mais rápido ao se aproximar. Mas uma vez reunidos, o tempo para ambos deve ser o mesmo. Sua ilusão de dilatação ou compressão do tempo é, portanto, uma função de como a taxa de expansão ou contração da distância entre eles afeta a transmissão de informações entre eles. Não tem nada a ver com o espaço que cada um ocupa ou sua posição em relação a qualquer outra posição no espaço e no tempo.
Consequentemente, qualquer ilusão desse tipo pode existir apenas enquanto houver uma quantidade variável de espaço entre eles. Portanto, não há razão para supor que seu irmão "estacionário", após a reunião de todos os três, não deveria ter a mesma idade que eles. De fato, se, ao serem reunidos, os trigêmeos não tivessem todos a mesma idade, então deve ser possível que dois pontos diferentes no tempo existam em um ponto no espaço-tempo, o que é um absurdo.
Ao contrário de suas relações com seu irmão no módulo estacionário, as jornadas dos dois trigêmeos viajantes formam uma simetria oposta perfeita. Cada um deles sofre as mesmas acelerações igualmente e opostamente. Uma vez que suas situações são totalmente simétricas, como o espaço-tempo decide qual dos dois trigêmeos viajantes deve ser mais jovem e qual deve ser mais velho que o outro quando se reunirem? Com base em que poderia haver qualquer assimetria entre suas idades após a jornada? A ideia da relatividade clássica de que um dos trigêmeos viajantes não deveria ter envelhecido tanto quanto o outro quando reunidos não é apenas um paradoxo: é um absurdo lógico.
Não obstante tudo o acima, como abordado em um um artigo anterior, a dilatação e compressão aparentes no tempo, durante as jornadas, só se manifestam para o tempo no plano perpendicular à linha de viagem. O tempo ao longo do eixo de viagem sofre apenas a ilusão de assimetria cíclica.
Temos de explorar o comportamento do módulo e dos seus fantasmas mais completamente. Contudo, para fazer isto, devemos ter muito cuidado sobre como representamos o parâmetro mais fundamental aqui implicado, a saber o tempo.
© 17 agosto 2006 Robert John Morton |
ANTE |
PROX


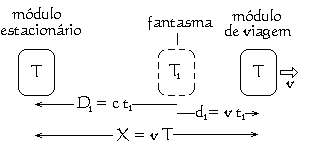

 A proporção entre a distância X (do módulo "em movimento") e a distância D (do seu fantasma) para o módulo "estacionário" varia inversamente à velocidade v do módulo "em movimento". As velocidade deles também deve estar nesta mesma proporção. O gráfico à esquerda usa esta proporção para traçar a velocidade do fantasma contra a velocidade do módulo "em movimento" em unidades de c, a velocidade da luz. Ignore somente, por enquanto, a "legalidade" física do módulo que viaja além da velocidade da luz. Vemos que, no entanto rápido o módulo viaja, o seu fantasma — que é para o observador a realidade física eficaz do módulo — nunca pode alcançar a velocidade da luz.
A proporção entre a distância X (do módulo "em movimento") e a distância D (do seu fantasma) para o módulo "estacionário" varia inversamente à velocidade v do módulo "em movimento". As velocidade deles também deve estar nesta mesma proporção. O gráfico à esquerda usa esta proporção para traçar a velocidade do fantasma contra a velocidade do módulo "em movimento" em unidades de c, a velocidade da luz. Ignore somente, por enquanto, a "legalidade" física do módulo que viaja além da velocidade da luz. Vemos que, no entanto rápido o módulo viaja, o seu fantasma — que é para o observador a realidade física eficaz do módulo — nunca pode alcançar a velocidade da luz.
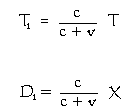 Do acima mencionado, vimos que — do ponto de vista do observador — o tempo no módulo "em movimento" dilata-se por um montante dado pela fórmula à direita.
Do acima mencionado, vimos que — do ponto de vista do observador — o tempo no módulo "em movimento" dilata-se por um montante dado pela fórmula à direita.
 No diagrama à esquerda, Dn é a distância da extremidade próxima do objeto fantasma do olho do observador a bordo do módulo "estacionário". Correspondentemente, Df é a distância da extremidade mais distante do fantasma. Df é maior que Dn por um valor igual ao comprimento da imagem fantasma do módulo "viajante". Portanto, a luz demora um pouco mais para alcançar o olho do observador do outro extremo do módulo de "viagem" do que do seu fim próximo. Esse tempo extra é L / c, onde L é o comprimento do fantasma.
No diagrama à esquerda, Dn é a distância da extremidade próxima do objeto fantasma do olho do observador a bordo do módulo "estacionário". Correspondentemente, Df é a distância da extremidade mais distante do fantasma. Df é maior que Dn por um valor igual ao comprimento da imagem fantasma do módulo "viajante". Portanto, a luz demora um pouco mais para alcançar o olho do observador do outro extremo do módulo de "viagem" do que do seu fim próximo. Esse tempo extra é L / c, onde L é o comprimento do fantasma.



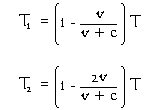 Além disso, a velocidade na qual o tempo é observado para passar é diferente para cada fantasma. O observador "estacionário" vê o tempo decorrido no relógio dentro do primeiro fantasma como T1, ao passo que o observador "em movimento" vê o tempo decorrido no relógio dentro do segundo fantasma como T2, como mostrado à direita. O observado módulo "em movimento" está movendo-se do observador "em movimento" duas vezes mais rápido que o módulo estacionário. Conseqüentemente, o relógio no segundo fantasma corre a apenas metade da velocidade do relógio no primeiro fantasma.
Além disso, a velocidade na qual o tempo é observado para passar é diferente para cada fantasma. O observador "estacionário" vê o tempo decorrido no relógio dentro do primeiro fantasma como T1, ao passo que o observador "em movimento" vê o tempo decorrido no relógio dentro do segundo fantasma como T2, como mostrado à direita. O observado módulo "em movimento" está movendo-se do observador "em movimento" duas vezes mais rápido que o módulo estacionário. Conseqüentemente, o relógio no segundo fantasma corre a apenas metade da velocidade do relógio no primeiro fantasma.
 O diagrama na esquerda mostra o módulo "em movimento" aproximando-se para o módulo "estacionário" à velocidade v. Abaixo dele são as fórmulas da distância D1 do fantasma e do tempo T1 mostrado no relógio neste fantasma. Em todos os meus cenários, até agora, considero a velocidade do módulo "em movimento" v que é constante. Conseqüentemente, a expressão c ÷ (c + v) é também constante. Isto significa que a velocidade do fantasma é sempre proporcional à velocidade do módulo "em movimento".
O diagrama na esquerda mostra o módulo "em movimento" aproximando-se para o módulo "estacionário" à velocidade v. Abaixo dele são as fórmulas da distância D1 do fantasma e do tempo T1 mostrado no relógio neste fantasma. Em todos os meus cenários, até agora, considero a velocidade do módulo "em movimento" v que é constante. Conseqüentemente, a expressão c ÷ (c + v) é também constante. Isto significa que a velocidade do fantasma é sempre proporcional à velocidade do módulo "em movimento".
