Robert John Morton
O Universo
Sobre Teorias
Tempo e Espaço
Éter Enigmatico
Objetos e Matéria
Noção de Movimento
Força e Inércia
Eventos e Ondas
Deslocação Vermelho
Revolução
Natureza da Luz
Vista Estabelecida
O Axioma Principal
Simultaneidade
Do Observador
Dilatação de Tempo
Quadro Da Fonte
Velocidade da Luz
O Efeito de Doppler
Onda ou Partícula?
Suponha que a luz era a parte da essência da sua fonte que se dispersou através do espaço. Então, seria plausível considerar a velocidade da luz como sendo relativa somente ao quadro de referência da sua fonte.
[English]
Classicamente, foi aceito que a luz deve viajar como uma perturbação progressiva dentro do quadro universal de referência de um éter luminífero. Esta idéia foi desacreditada, porque a luz parecia atravessar o espaço entre qualquer fonte e qualquer observador em uma velocidade universalmente fixa c. Esta velocidade parecia ser independente da velocidade relativa da fonte, observador e o resto do universo. Foi posteriormente teorizado que a luz sempre viajava na sua velocidade universalmente fixa c, do ponto da vista de qualquer observador que se movia com uma velocidade constante. Já exploramos a visão centrada deste observador da propagação da luz na nossa seção prévia.
Contudo, a idéia de que a velocidade da luz parece ser a mesma sob os pontos da vista de todos os observadores que estão se movendo com a velocidade constante é também problemática. Isto é porque a aparente distância das viagens de luz, indo da sua fonte a um observador, diferenciam-se segundo consideramos o processo do ponto da vista da fonte ou do ponto da vista do observador. O mesmo é verdadeiro durante o tempo que ela gasta. A Teoria da Relatividade parece contornar esse problema por postulando que o espaço fica contratado por montantes diferentes, dentro dos quadros de referência de observadores diferentes, segundo a sua velocidade relativa à fonte da luz. Esta postulação também requeria que o tempo ficasse dilatado.
Não obstante, acredito que há um modo mais plausível para interpretar a observação que deve ser considerada. Primeiramente, vamos olhar novamente para a passagem da luz entre a fonte e o observador, do ponto da vista de um observador arbitral.
Um observador está observando uma fonte de luz. Ela está afastando-se do observador em uma fração significante v da velocidade da luz. No espaço livre sabemos que a velocidade é relativa. Conseqüentemente, não importa se nós pensamos que o observador está "estacionário" e a fonte de luz está "em movimento" ou se pensamos que a fonte de luz está "estacionária" e o observador está "em movimento". Qualquer desses dois pontos de vista que escolhemos não deve fazer, em princípio, nenhuma diferença no modo como a luz viaja entre a sua fonte e o observador. Se aceitarmos que a luz viaja à velocidade c em todas os quadros de referência em movimento uniforme, então, para qualquer observador da fonte de luz esses dois pontos de vista serão como se segue.
O caso onde consideramos a fonte de luz em movimento é mostrado à direita. Um pulso de luz viaja da posição no Quadro de Referência do observador, onde foi emitido pela fonte de luz. Ele atravessa o espaço daquele ponto a onde o observador está localizado "na origem" do sistema de coordenada do seu Quadro de Referência. Ele atravessa este espaço na velocidade c em tempo t. A distância que ele viaja é, por isso, c × t. Durante o tempo t, a fonte de luz "em movimento" viaja a uma distância v × t mais além do observador, onde v é a velocidade relativa entre o observador e a fonte de luz. Ao tempo em que o pulso de luz alcança o observador, este o verá como vindo da posição aonde a fonte de luz estava, quando ela emitiu o pulso de luz.
As conseqüências disto são como se segue. O observador vê só um fantasma da fonte de luz como se ela estivesse e onde estivesse em um montante do tempo t no passado. O observador não tem nenhum capacidade de ver a fonte de luz como está "agora" e onde está "agora". Pelo termo "agora" significo "o instante em que o observador está recebendo a luz". A distância em qualquer instante dado entre o observador e a realidade atual da fonte de luz é (v + c) × t.
À esquerda é mostrada a situação inversa onde consideramos estar a fonte de luz "estacionária" e o observador "em movimento". Um pulso de luz é emitido pela fonte de luz. Ele viaja na velocidade c em direção ao observador. Enquanto o pulso de luz está viajando em direção ao observador, o observador está movendo-se cada vez mais distante da fonte de luz na velocidade v. Assim, ao tempo em que o pulso de luz alcança o observador, ele viajava a uma distância v × t a mais da fonte de luz. Durante este mesmo montante de tempo t, o pulso de luz viajava a uma distância c × t. Assim, nesta situação, a distância entre a realidade da fonte de luz e o observador é simplesmente c × t e não (v + c) × t. Além disso, o observador percebe a fonte de luz estar "agora" onde de fato está "agora", embora ele a veja, como se estivesse, num montante de tempo t no passado.
Por favor, observe que a distância (c + v) × t, na primeira situação, é a mesma distância que c × t na segunda situação. Portanto, o t é um maior montante de tempo na segunda situação. Vamos agora comparar essas duas situações, supostamente equivalentes e cambiáveis, descritas acima.
Quando consideramos estar o observador "estacionário" e a fonte de luz "em movimento", o observador percebe estar a fonte de luz:
Quando consideramos estar o observador "em movimento" e a fonte de luz "estacionária", o observador percebe estar a fonte de luz:
Claramente, essas duas situações não são equivalentes e cambiáveis. Temos um paradoxo evidente. Este paradoxo fica mais complicado mesmo quando consideramos o experimento clássico do Relógio de Luz.
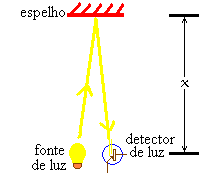Um relógio de luz compreende uma fonte de luz, um espelho colocado a uma distância fixa x longe da fonte e um detector ao lado da fonte de luz. Este arranjo está ilustrado à direita. A fonte de luz é provocada eletronicamente para emitir um pulso muito curto de luz. A luz viaja até o espelho de onde é refletido atrás no detector. O detector emite um pulso elétrico que provoca a fonte de luz para emitir o próximo pulso de luz. O período do relógio, isto é, a duração do tic-tac do relógio é o montante do tempo requerido pela luz para viajar a distância 2x em direção ao espelho e retornar. Devemos fazer a distância x muito grande para que os atrasos no gatilho eletrônico sejam negligenciável em comparação com o tempo levado pela luz para viajar até o espelho e retornar.
O diagrama mostra as trajetórias da ida e da volta do pulso de luz com um pequeno ângulo entre um trecho e o outro. Isto está somente para esclarecer a ilustração. O intento é que a fonte de luz e o detector devem ser tão pertos quanto possível, de modo a ida do pulso pode seguir exatamente a mesma linha que a volta.
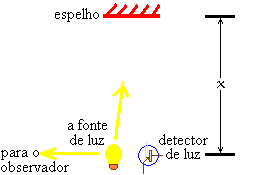A mesma fonte de luz que envia o pulso de luz na direção do espelho também envia um pulso de luz em direção ao observador, como mostrado à esquerda. A emissão deste pulso marca a partida de um novo período do relógio. Depois, quando o pulso de luz volta do espelho e entra no detector, este provoca a fonte de luz novamente para enviar outro pulso. A emissão deste segundo pulso marca o fim deste período do relógio e a partida do próximo pulso. Este segundo pulso também viaja em direção ao observador, chegando um tanto mais tarde.
Vamos agora virar o relógio na posição horizontal. Isto é mostrado à direita. O diagrama do relógio foi simplificado. Um observador observa como o contador eletrônico do relógio conta os períodos do relógio. O observador está estacionário em relação ao relógio. Se o observador e o relógio estão estacionários ou se estão móveis em conjunto na mesma velocidade v é irrelevante ao período do relógio observado pelo observador.
Ignorando os atrasos "negligenciáveis" na eletrônica do relógio, o período do tic-tac do relógio será 2 × x ÷ c segundos. Agora suponha que o relógio está afastando-se do observador na velocidade v, como representado abaixo.
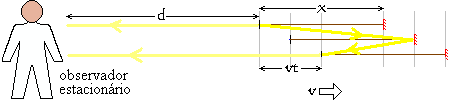
No mesmo instante em que o pulso de luz deixa a fonte de luz, a informação deste evento deixa a fonte de luz também. Esta informação atravessa a distância d entre a fonte de luz e o observador à velocidade da luz, c.
No quadro de referência do observador, nós podemos ver que no momento em que a luz alcança o espelho, este viajou uma distância ½(v × t) mais além disso. O espelho reflete a luz. Mas agora ele não tem de ir mais longe. Isto é porque até ao fim do período do tic-tac do relógio t, o detector de luz viajou uma distância v × t maior além do observador. Não obstante, a distância real viajada pela luz (no quadro de referência do observador) é ainda 2x, como estava para o observador "em movimento", no caso acima. Vamos confirmá-lo. Para alcançar o espelho, a luz viaja uma distância x + ½ (v × t). Para regressar do espelho ao detector, o pulso de luz viaja uma nova distância de x - ½(v × t). Portanto, a distância total que ele viaja é 2x. Assim, não há nenhuma necessidade de contração do espaço e dilatação do tempo para explicar este fenômeno.
Quando o pulso de luz chega ao detector de luz, a informação deste evento empreende a sua viagem do detector ao observador. Esta informação, contudo, deve viajar uma distância de d + v × t. Portanto, a informação que avisa ao observador do fim da tic-tac do relógio deve viajar uma distância v × t além disso do que a informação que o avisou do início do tic-tac do relógio. Isto significa que o período do tic-tac do relógio, do ponto de vista do observador, é (2x + v × t) ÷ c segundos ao invés do simples 2 × x ÷ c segundos, como foi para o observador "em movimento".
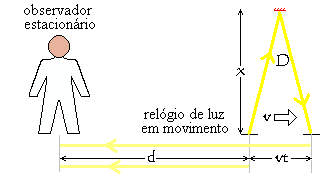Vamos agora virar o relógio de luz "em movimento" da posição horizontal para vertical, de modo que o seu pulso de luz vai e volta do espelho em uma direção perpendicular em relação à direção do observador "estacionário". Considere o caminho do pulso de luz do relógio dentro do quadro de referência do observador. Ao tempo em que o pulso de luz da fonte chega ao espelho, o próprio espelho moveu uma distância ½(v × t) a mais à direita. Então, ao tempo em que o pulso de luz refletido fez a viagem de regresso e alcançou o detector, o próprio detector moveu a distância cheia de v × t de onde estava quando o pulso de luz originalmente deixou a fonte.
Isto significa que, dentro do quadro de referência do observador "estacionário", o pulso de luz do relógio viaja a distância D, dado pela fórmula mostrada no diagrama à esquerda. Esta fórmula é conseguida aplicando o Teorema de Pitágoras a uma metade do triângulo isósceles formado pelo caminho do pulso de luz e a linha da base e, então, dobrando o resultado.
Deste raciocínio, pareceria que o período do tic-tac do relógio de luz, como percebido pelo observador "estacionário", seria (D + v × t) ÷ c segundos.
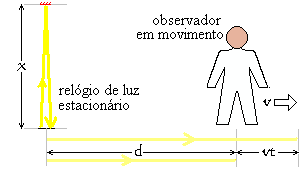A velocidade é um conceito relativo. Isto significa que nós somos livres para trocar quem consideramos estarem "estacionários" e quem consideramos estarem "em movimento". Então agora, considerem o relógio de luz estando "estacionário" e o observador "em movimento" em relação ao relógio de luz, como mostrado à direita. A diferença nos tempos de chegada ao observador entre os sinais que marcam o início e o fim de um tic-tac do relógio é agora só (2 × x + v × t) ÷ c segundos. A diferença quantitativa entre este período e o período (D + v × t) ÷ c (para o relógio "em movimento" obtido acima) não é importante. O que é importante é simplesmente que eles são diferentes.
Cada um pode argumentar que a razão da diferença é que estamos considerando a situação sob os pontos de vista de dois quadross de referência diferentes. Contudo, se houvesse um milhão de observadores diferentes, cada um viajando em uma velocidade e direção diferentes, com respeito ao relógio de luz, haveria um milhão de valores diferentes de D da passagem da luz dentro de um único relógio. Cada observador também perceberia um período diferente do tic-tac do relógio quando o relógio "em movimento" estivesse em linha com relação ao observador, comparativamente com quando o relógio estivesse na perpendicular ao observador ou em algum outro ângulo.
A presença de todos esses observadores assim contratam o espaço e dilatam o tempo dentro da vizinhança deste relógio único? Este relógio de luz existe efetivamente em uma superposição diferente do estado dentro de um milhão de universos diferentes?
Com respeito ao relógio de luz, um observador é passivo. Para todos os objetivos práticos, ele não tem nenhum efeito no relógio. Conseqüentemente, o trânsito da luz da fonte ao espelho e do retorno ao detector não está, de modo nenhum, sob o efeito da sua presença ou da presença de muitos observadores que possamos considerar. Além disso, durante a sua viagem da fonte ao espelho e do retorno ao detector, a luz dentro do relógio de luz não é observável pelo observador. A luz nasce, vive e morre dentro dos limites do relógio. Qualquer observador só pode observar sinais de informações, isto é, ele pode experimentar a chegada de ondas de luz que estão viajando diretamente em direção a ele. Tais fenômenos que viajam em qualquer outra direção não faz parte do seu universo de experiência.
O fato de que o observador está modificando constantemente a sua posição - e por isso o seu ponto de vista - enquanto a luz está viajando entre a fonte, o espelho e o detector não faz de, nenhum modo, influi no movimento da luz. Exatamente porque o observador percebe que o relógio está movendo-se lateralmente não significa que a própria luz tem um verdadeiro componente lateral ao seu movimento.
Isto significa que, do ponto de vista de qualquer um, considerando-se o movimento do relógio e do observador, a luz realmente viaja a uma distância 2x dentro do relógio, em um tempo t = 2 × x ÷ c. A comunicação da informação ao observador sobre o tempo de partida e o tempo de chegada de um tic-tac de relógio é uma transação física inteiramente separada.
A luz usada para o relógio de luz e a luz usada para sinalizar ao observador têm a mesma fonte. No entanto, a luz recebida pelo observador viaja em uma direção diferente da luz usada pelo relógio de luz. A luz dentro do relógio de luz não é observável pelo observador. Ele é fundamentalmente incapaz de ter qualquer noção de sua existência ou de sua jornada. Está fora de seu universo de experiência. Está fora de seu quadro de referência. Apenas a luz viajando por caminhos que cruzam sua posição no espaço e no tempo pode ser detectada e experimentada por ele. Ele não pode ter conhecimento ou conexão com a luz viajando em outro lugar.
Um observador não tem nenhum modo de perceber a aproximação de um pulso de luz. Ele não tem nenhum modo de perceber quando o pulso deixou a sua fonte. Ele não tem nenhum modo de perceber a que distância o pulso viajou. Ele não tem nenhum modo de perceber a que velocidade o pulso está viajando em direção a ele. Ele só pode percebê-lo quando o pulso conseqüentemente "bate" nele. Mesmo assim, ele não tem nenhum modo de perceber a velocidade do seu impacto.
É fundamentalmente impossível para um observador observar um "fóton" em trânsito de sua origem para qualquer destino [incluindo ele mesmo].
A única coisa que um observador pode experimentar como o resultado de um pulso de luz que chega é uma modificação forçada no campo de força elétrica ou magnética na sua imediação. E esta modificação no campo de força é, de fato, perpendicular (ângulo reto) à direção da qual a luz veio. Conseqüentemente, desde que o movimento da onda transversal da luz não implica nenhum movimento material na direção em que a onda está "viajando", a noção de que a onda tem uma velocidade "de impacto" com o observador é essencialmente sem sentido.
Um observador, por isso, não pode deduzir nada dentro do seu quadro de referência sobre a velocidade que a luz teve durante a sua viagem. Ele não teve nenhum controle ou influência na fonte da luz na hora em que a luz foi criada. Conseqüentemente, a luz que um observador recebe não tem nenhuma razão ou motivação para atar a sua velocidade de qualquer modo ao quadro de referência de um observador.
Isto reforça a noção de que o único quadro de referência dentro da qual a luz viaja na velocidade c é aquela da sua fonte.
Vamos voltar a considerar o observador que observa uma fonte de luz. Novamente, a fonte está afastando-se dele em uma fração significante da velocidade da luz. Como antes, no espaço livre sabemos que a velocidade é relativa. Conseqüentemente, não há problema se pensamos no observador como "estacionário" e a fonte de luz como "em movimento" ou se pensamos na fonte de luz como "estacionária" e o observador como "em movimento". Qualquer um desses dois pontos de vista que escolhermos não deve fazer, em princípio, nenhuma diferença no caminho das viagens da luz entre a sua fonte e o observador.
Agora, contudo, não podemos aceitar que a luz viajar com a velocidade c em todas os quadros de referência. Em vez disso, precisamos aceitar que a luz viaja com a velocidade c só dentro do quadro de referência da sua fonte. Se aceitarmos isto, então, para qualquer observador da fonte de luz esses dois pontos de vista serão como se segue.
O caso no qual a fonte de luz está em movimento é mostrado à direita. Um pulso de luz viaja da origem do quadro de referência da fonte onde foi emitido. Ele atravessa o espaço daquele ponto a onde o observador está localizado quando a luz alcança-o. Ele atravessa este espaço na velocidade c no tempo t. A distância em que ele viaja é, por isso, c × t. Durante o tempo t, a fonte de luz "em movimento" viaja a uma distância v × t a mais ao observador, onde v é a velocidade relativa entre o observador e a fonte de luz. No momento em que o pulso de luz alcança o observador, o observador vê que veio da posição a onde a fonte de luz de fato então está.
Contudo, o observador verá, então, a fonte de luz como estava quando o pulso de luz a deixou. O observador verá a fonte de luz como ela apareceu t (unidades do tempo) no passado.
À esquerda é mostrado a situação inversa onde consideramos a fonte de luz como "estacionária" e o observador para como "em movimento". Um pulso de luz é emitido pela fonte de luz. Ele viaja na velocidade c em direção ao observador. Enquanto o pulso de luz está viajando em direção ao observador, o observador está movendo-se sempre mais distante da fonte de luz na velocidade v. Assim que o pulso de luz alcança o observador, ele foi viajar a uma distância v × t mais distante da fonte de luz. Durante este mesmo montante de tempo t, o pulso de luz viajou a uma distância c × t.
Assim, nesta situação, a distância entre a realidade da fonte de luz e o observador é novamente c × t. O observador novamente percebe a fonte de luz estar "agora" aonde ela realmente está "agora", embora ele a veja como se estivesse em um montante do tempo t no passado.
Então deste modo de examinar o processo, os dois pontos de vista acima são idênticos. Não há nenhum paradoxo. Esta visão centrada na fonte também evita o paradoxo do relógio de luz "perpendicular", onde o período do relógio seria diferente, segundo o qual é considerado como "estacionário": o observador ou o relógio.
Isto leva-nos a considerar a luz simplesmente como a parte da sua fonte. Uma fonte de luz é uma estrutura microscópica de energia capturada. Quando ela emite a luz, a fonte dispersa a parte da sua essência no resto do universo como uma perturbação eletromagnética que diverge. A velocidade com a qual esta perturbação viaja, por isso, deve ser relativa à sua fonte.
Isto sugere que a luz deva ser, essencialmente, uma extensão que se dispersa da sua fonte. Antes de que a luz seja emitida, a sua energia é uma parte daquela que é mantida prisoneira dentro da estrutura da sua fonte. Depois que a luz é emitida, a sua energia é lançada no universo como uma perturbação em constante expansão. O montante da energia nesta perturbação é o montante da energia lançada pela fonte. Disto, pareceria razoável supor que a quantidade da energia lançada pela fonte, em qualquer dada transação de emissão, seria determinada apenas pela natureza, estrutura e mecanismo da sua fonte microscópica.
Embora a visão centrada na fonte parece funcionar para a luz, não é consistente com qualquer visão de outros fenômenos observáveis, como a gravidade. Não obstante, há outra maneira de construir uma visão de luz centrada no observador, o que é consistente com uma visão complementar da gravidade.
Fundamentalmente, um observador nunca pode honestamente afirmar que qualquer luz que ele esteja vendo foi ativamente emitida por uma fonte. Ele só pode honestamente afirmar que uma imagem em sua retina, do que parece ser um objeto remoto, está chegando a ele daquele objeto remoto. Assim, pragmaticamente, ele só pode deduzir que a luz de todos os objetos visíveis dentro de seu horizonte de eventos está convergindo em sua direção a partir das respectivas direções no espaço de todos aqueles objetos aparentes. A questão é: como ela está sendo trazida?
Em meus nove ensaios sobre o Universo, construí gradualmente uma visão centrada no observador com base na noção de que o universo é feito de um fluido de velocidade onipresente, ao qual me refiro como éter. Este éter é conceitualmente muito diferente do antigo éter luminífero mencionado no início deste ensaio. Eu me refiro a ele como um fluido de velocidade porque ele só pode existir enquanto viaja na velocidade da luz. Além disso, ele só se manifesta para objetos que estão acelerando. Ele não interage de forma alguma com objetos que viajam em velocidade relativa constante. Ele flui convergentemente, na velocidade da luz, para buracos nanoscópicos postulados, dos quais todos os constituintes fundamentais da matéria consistem.
Nesta visão, que é exposta completamente no meu ensaio intitulado Eventos e Ondas, uma fonte de luz grava tensões inerciais bipolares no influxo etéreo de passagem do observador. O éter de passagem flui radialmente para dentro em direção ao observador na velocidade da luz, carregando as gravuras inerciais bipolares com ele. Necessariamente, nesta visão, a velocidade da luz, c, está bem e verdadeiramente ligada ao observador.
Não obstante, se simplesmente transpormos a visão centrada na fonte acima [descrita acima] para uma centrada no observador, a geometria e a matemática não mudam e o paradoxo do relógio de luz desaparece.
Tudo o que requer é que, quando a fonte grava sua inscrição no éter que passa, essa gravação não esteja mais obrigada a viajar da fonte na velocidade c. Em vez disso, ela deve sempre viajar em direção ao observador na velocidade c. E isso ocorre porque, nessa visão, a luz não tem velocidade. Ela não viaja: ela é transportada para o observador como uma gravação inercial bipolar em seu influxo etéreo que está sempre convergindo em sua direção, de todas as direções, na velocidade da luz.
