Robert John Morton
O Universo
Sobre Teorias
Tempo e Espaço
Éter Enigmatico
Objetos e Matéria
Noção de Movimento
Força e Inércia
Eventos e Ondas
Deslocação Vermelho
Revolução
Natureza da Luz
Vista Estabelecida
O Axioma Principal
Simultaneidade
Do Observador
Dilatação de Tempo
Quadro Da Fonte
Velocidade da Luz
O Efeito de Doppler
Onda ou Partícula?
Esta visão afirma que o axioma, de que as leis da física deve parecer o mesmo para todos os observadores, exige que a velocidade da luz seja a mesma em todos os quadros de referência. Isso, por sua vez, leva a noções contra-intuitivas como a dilatação do tempo e a contração do comprimento. [English]
Classicamente, assumiu-se que a luz deve viajar como um distúrbio progressivo dentro de um meio fluido de uma maneira semelhante à forma como as ondas sonoras viajam pelo ar. Eles chamaram esse meio do éter luminífero. Deve necessariamente permear todo o espaço - incluindo o espaço entre os átomos de materiais transparentes.
O problema-chave levantado pelo éter luminífero era que se tornaria um quadro de referência universal fixo ao qual a velocidade da luz deveria estar ligada. Todos os corpos celestes moveriam-se em relação a este éter. Conseqüentemente, a velocidade a que a luz translada-se entre objetos celestiais variaria de acordo com a velocidades e direções dos objetos. Além disso, o movimento de todos os corpos celestes, através do éter, produzia uma onda de proa e arrasto - assim como um navio faz quando viajando atravessa o oceano. A observação experimental, no entanto, mostrou que a velocidade da luz não variou de direção e que parecia ser independente do movimento de suas fontes e seus observadores.
Por conseguinte, postulou-se que a luz movia-se a uma velocidade universalmente fixa em relação a cada observador. Esta velocidade universal da luz é normalmente denotada pela letra c. A luz emitida por uma única fonte embarcaria assim na jornada a uma velocidade c longe da fonte. Em seguida, abordaria o seu destino (observador) na mesma velocidade universal c, independentemente da velocidade que o destino (observador) viaja em relação à fonte. A única maneira de reconciliar a geometria dessa relação foi postular que o espaço da fonte se contraiu e seu tempo se dilatou do ponto de vista do observador.
Eu penso que Einstein estava andando em um bonde (ou ônibus elétrico) ao longo de Kramgasse em Berna, na Suíça. Ele olhou de volta para a famosa torre do relógio retrocedendo dele. Então ele pensou em como a hora do relógio lhe apareceria se o seu bonde passasse longe do relógio em uma proporção significativa da velocidade da luz.
Quanto mais longe ele se afastasse do relógio, a mais tempo a luz do relógio precisaria para alcançá-lo. O efeito desse atraso acumulado seria fazer com que o relógio pareça estar sendo executado mais devagar do que o normal. Se ele tivesse um relógio de bolso, ele veria as mãos do relógio da torre ficando cada vez mais atrás das mãos de seu relógio de bolso. O único motivo pelo qual o relógio da torre parece estar funcionando devagar é que a luz não viaja instantaneamente do relógio para os olhos de Einstein. Viaja a uma velocidade finita e, portanto, leva um tempo finito para chegar. Quando as mãos do relógio se movem, a luz do relógio faz uma quantidade cada vez maior de tempo para intimar a nova posição das mãos do relógio para Einstein. Em outras palavras, é apenas porque a luz viaja a uma velocidade finita. É definitivamente NÂO porque o relógio está realmente lento.
Do ponto de vista de alguém em frente à torre do relógio, o relógio está funcionando a velocidade normal. Do ponto de vista de um observador que fica um ano-luz longe da torre do relógio, mas cuja velocidade relativa à torre do relógio é zero, o relógio está funcionando a velocidade normal. A hora em que este observador vê o relógio como indicando, no entanto, ficará um ano atrás do que as mãos do relógio estão mostrando ao observador diretamente em frente à torre do relógio.
Por mais lento que o relógio da torre pareça estar a correr do ponto de vista de Einstein no seu bonde super-rápido, o relógio de si mesmo, do ponto de vista dos observadores "estacionários" onde quer que estejam, está funcionando no normal rapidez. A observação de Einstein do relógio da torre a partir de seu ponto de vista de alta velocidade não modifica de modo algum tempo, espaço ou movimento na vizinhança do relógio da torre. Não há nada de estranho nem perplexo sobre tudo isso até agora.
As coisas só começam a ficar estranhas quando examinamos a diferença entre os significados das palavras "aparece" e "é" no contexto de Einstein viajando em seu bonde super-rápido longe da torre do relógio de Kramgasse. Isso ocorre porque a velocidade da luz não é apenas a velocidade na qual as posições atuais das mãos do relógio são comunicadas a Einstein em seu bonde super-rápido. É, mais profundamente, a velocidade com que todos os efeitos físicos propagam-se para Einstein enquanto viaja em seu bonde super-rápido
Estamos bem conscientes de que freqüêntamente as coisas não são como elas aparecem, especialmente no domínio das relações humanas. Aqui, no entanto, precisamos considerar somente os fenômenos puramente físicos. Um exemplo físico de algo que não é como parece é uma miragem. Um intuitivamente sabe que os camelos geralmente não andam de cabeça para baixo em um lago azul brilhante. É uma ilusão óptica causada por um gradiente de temperatura superior ao normal no ar próximo ao solo. Em outras palavras, o meio através do qual a luz viaja dos camelos para o observador está modificando a aparência da cena. A realidade é que os próprios camelos estão andando de pé na areia.
A observação de Einstein de que o relógio na torre de Kramgasse está a correr devagar não é uma miragem no sentido normal. É fundamentalmente diferente. Isso ocorre porque as propriedades do espaço não determinam apenas a velocidade a que a luz pode viajar. Eles fazem da mesma velocidade o limite no qual qualquer coisa pode viajar. Por exemplo, se a torre do relógio fosse um planeta o que de repente deixasse de existir, o seu efeito gravitacional sobre Einstein cessaria somente quando o planeta desapareceu visivelmente. Isso aconteceria apenas após o período necessário para a luz viajar do planeta para Einstein. Para Einstein, é como se toda a realidade fosse uma miragem. Consequentemente, do ponto de vista de Einstein, o que ele vê é a realidade. No universo pessoal de Einstein, o relógio na torre em Kramgasse está, em realidade, funcionando lentamente.
É importante perceber que a situação inversa também é verdadeira. No universo de um observador em pé na frente da torre do relógio em Kramgasse, o relógio da torre está funcionando a velocidade normal e é o relógio de bolso de Einstein que está funcionando devagar. A dilatação do tempo é algo que ocorre para qualquer observador de qualquer relógio que se mova em direção ou afastado dele a qualquer velocidade.
O famoso experimento de pensamento, envolvendo um relógio de luz, foi construído para ilustrar como isso deveria acontecer. No diagrama abaixo, os retângulos cinza representam um par de espelhos. Os espelhos se encaram. Eles são montados em um quadro comum para que eles permaneçam sempre a mesma distância fixa entre um ao outro.
No meio de um dos espelhos é um pequeno orifício através do qual brilha uma fonte de luz perfeitamente colimada, como um laser perfeito. A fonte de luz emite um flash inicial de luz. A luz viaja para o espelho superior. Lá, ele é refletido de volta para o espelho inferior, que depois o reflete novamente no espelho superior. Assim, a luz continua para sempre refletindo entre os dois espelhos. A luz viaja no caminho entre os dois espelhos à velocidade c. O período do relógio é definido como o tempo que leva o flash da luz para fazer a ida e volta do espelho inferior para o espelho superior e vice-versa. Este é o dobro do tempo t que a luz leva para percorrer um trecho entre um espelho e o outro. O período do relógio de luz é, portanto, 2t. Conseqüentemente, a distância que a luz viaja durante um período do relógio é de 2ct.
Para fazer uso desse relógio, seria necessário monitorar os seus tique-taques. Isso requer a intervenção de algum tipo de detector para determinar cada instante quando a luz atinge o espelho inferior. No mundo real, isso desperdiçaria a energia do flash da luz, então desapareceria gradualmente. Teria que haver algum meio de causar um flash de desvanecimento para ativar um novo flash. Não obstante, este é apenas um experimento de pensamento, então nosso detector pode ser imaginário. E um detector imaginário não consome energia.
O próximo estágio deste experimento de pensamento é considerar o que acontece se o relógio estiver em movimento em relação a um observador a uma velocidade v, que é uma proporção significativa da velocidade da luz.
Na versão tradicional deste experimento de pensamento, o observador está olhando diretamente para a tela ou página, como você está fazendo agora, e a montagem do relógio está movendo-se pela página da esquerda para a direita. No entanto, a mesma geometria seria realizada para um observador colocado nos lados esquerdo ou direito do diagrama, ou mesmo em qualquer lugar no plano horizontal que cortaria o diagrama ao meio. Isso é porque estou considerando apenas o que está acontecendo dentro do próprio relógio e não como a informação sobre o estado atual do relógio é transmitida ao observador.
No tempo t requerido pela luz para viajar de um espelho para o outro, a montagem do relógio move uma distância vt para a direita. Do ponto de vista do relógio, a luz simplesmente viaja a uma distância ct direta de um espelho para o outro. No entanto, do ponto de vista do observador, o espelho oposto moveu uma distância vt para a direita durante o período t. No quadro de referência do observador, a luz, portanto, tem que percorrer uma distância ct0 para chegar ao espelho oposto.
O cálculo do período do relógio de luz do ponto de vista do observador é uma simples aplicação do Teorema de Pitágoras ao triângulo de ângulo reto do qual a distância ct0 é a hipotenusa. A fórmula para o período completo ou cheio do relógio, do ponto de vista do observador, é mostrada na parte inferior direita do diagrama acima. É um algo maior do que 2t, o período do relógio desde o ponto de vista do próprio relógio. Do ponto de vista do observador, portanto, o relógio está sendo executado muito mais devagar.
Tradicionalmente, o propósito do experimento de pensamento acima não era mostrar que um relógio de luz "em movimento" corre lentamente dentro do quadro de referência de um observador "estacionário". O objetivo era mostrar que se a velocidade da luz sempre for a mesma em todos os quadros de referência, então o tempo no quadro de referência "em movimento" é sempre dilatado em relação ao quadro de referência "estacionário" do observador.
No entanto, para o propósito deste ensaio, desejo continuar considerando a forma como o próprio relógio de luz se comporta em situações diferentes.
Suponha que eu gire a montagem do relógio de luz através de um ângulo reto, ou seja, um quarto círculo ou 90° como mostrado abaixo.
A geometria mostra que, embora a montagem do relógio ainda esteja viajando da esquerda para a direita na velocidade v (uma fração significativa da velocidade da luz), a dilatação do tempo muda com a direção da luz. No trecho para frente, a luz viaja uma distância de ct0f = ct + vt no tempo t(1 + v/c), enquanto que no trecho reverso ela viaja uma distância de ct0r = ct - vt no tempo t(1 - v/c). O caminho total da luz no espaço do observador d = ct0f + ct0r = ct + vt + ct - vt, que é simplesmente 2ct.
O período completo do relógio é, portanto, 2t, o mesmo que se o relógio estivesse estacionário. Assim, o relógio de luz em linha, do ponto de vista do observador, corre em velocidade normal. Um resumo das distâncias e durações das jornadas da luz entre os espelhos é mostrado na tabela a seguir.
| Período | Distância | Duração |
|---|---|---|
| 1º Semi-período | ct + vt | t(1 + v/c) |
| 2º Semi-período | ct - vt | t(1 - v/c) |
| Período Total | ct + vt + ct - vt = 2ct | 2t |
O tique-taque do relógio de luz transversal é simétrica. Cada semi-período é da mesma duração. O relógio de luz em linha, no entanto, não faz tique-taques simetricas. A primeira semi-período (o tique) é mais longo do que o segundo semi-período (o taque). Parece estranho que o tempo se dilate por duas montantes diferentes ao longo do ciclo do relógio, enquanto a velocidade relativa entre o relógio e o observador permanece constante.
Suponha que dois relógios de luz idênticos sejam instalados em uma nave espacial. Um está montado transversalmente, ou seja, através de um diâmetro da nave espacial. O outro é montado longitudinalmente, isto é, ao longo do eixo central da nave espacial.
A nave espacial decola da Terra e mantém um curso diretamente distante da Terra. Para um observador na Terra, o relógio transversal está lento e o relógio longitudinal está funcionando à taxa normal.
Isso implica que, dentro do quadro de referência do observador, enquanto o tempo está funcionando a uma taxa normal, em linha com a rota da nave espacial, ele está sendo executado lentamente dentro do plano perpendicular à linha da rota. Essa situação será exatamente a mesma coisa quando a nave espacial retornar. O tempo em linha com a rota sempre passará normalmente, enquanto o tempo dentro do plano diametral da nave espacial irá, novamente, sempre passar mais devagar.
Que conseqüências isso tem para os relógios biológicos da tripulação da nave espacial? Como a tripulação envelhecerá durante uma ida e volta a uma estrela próxima e voltará numa fração significativa da velocidade da luz? Desprezando os efeitos gravitacionais para o momento, todos os aspectos da biologia da tripulação, que oscilar em linha com a direção daTerra, envelhecerão na taxa normal como na Terra. Os aspectos da biologia da tripulação que oscilar em qualquer outra orientação envelhecerão progressivamente mais lentamente à medida que as orientações destas oscilações aproximam-se do plano diametral da nave espacial.
Em outras palavras, cada membro da tripulação envelhecerá verticalmente mais lentamente do que envelhecerá horizontalmente. Se um membro da tripulação tiver um gêmeo que permaneceu na Terra durante a viagem, então seu gêmeo verá seu irmão ser mais novo que ele apenas na direção vertical. Este efeito não é simplesmente em uma escala macroscópica. Ele penetra até a granularidade mais fina do espaço. Cada átomo - então, cada "corda" - deve "oscilar" mais lentamente em uma dimensão do que nos outros dois, o que é claramente um absurdo físico.
Se os dois relogios de luz funcionam a taxas diferentes de acordo com a orientação para a direção do movimento, como comportar-se-ia um antigo mecanismo de relojoaria, com roda oscilatória e mola espiralada, nesta situação? Se o eixo da roda oscilatória estiver no plano diametral da nave espacial, ela girará mais devagar do que se ela estiver giranda em linha com o eixo da nave espacial? Eu penso que não.
No experimento de pensamento anterior, o observador não pode ter sido humano. Ele deve ter sido algum tipo de ser onipotente. Isso é porque, para que o observador tenha observado a taxa do relógio de luz em cada caso, ele teria que poder observar todos os pontos no espaço em cada instante. Eu não considerava como as informações sobre o estado atual do relógio, em qualquer momento, chegariam do relógio de luz viajando para um observador humano na Terra através do espaço real.
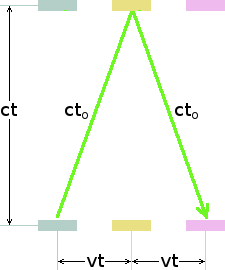Você, um observador humano, observe a versão transversal do relógio de luz passando através o seu campo de visão da esquerda para a direita a uma velocidade v, que é uma fração significativa da velocidade da luz. Um detector de luz está ligado a cada espelho. Isso desencadeia uma fonte de luz separada, que envia um breve flash na direção do observador sempre que o próprio flash de sincronização do relógio atinge o espelho ao qual está anexado. Você, portanto, vê um flash de luz alternadamente de cada espelho. Você, portanto, vê um flash para cada semi-período do relógio de luz. Mas os flashes que você vê não chegam no instante em que são emitidos pelo flasher no espelho em questão.
Eles exigem um montante de tempo T para percorrer o espaço entre você e o relógio.
Os dois espelhos continuam a uma distância constante de você enquanto eles atravessam o seu campo de visão da esquerda para a direita. O tempo T para cada flash para chegar será, portanto, constante. Você verá, portanto, este relógio funcionando à taxa mais lento que normal como calculada anteriormente. Mas suponha que você observe o relógio enquanto como ele está vindo diretamente em sua direção na velocidade v. Qual será o período do relógio do seu ponto de vista neste situação?
Conforme mostrado no diagrama a seguir, o semi-período dilatado t0 do relógio de luz viajando é o mesmo. No entanto, o flash que você vê no espelho inferior levará mais tempo para alcançá você do que o flash do espelho superior quando ocorrer. Isto é porque, no momento em que o flash do espelho superior ocorre, o relógio movará uma distância vt mais perto de você. O flash do espelho superior aparecerá para você ocorrer um pouco mais cedo δt do que ele deveria fazer. Você perceberá, portanto, que o semi-período do relógio é apenas t0 - δt.
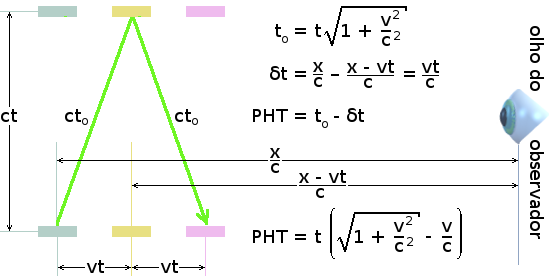
Se o relógio de luz for uma distância x de você quando o primeiro flash do espelho inferior ocorrer, então, quando o flash aparecer no espelho superior após o primeiro semi-período, o relógio de luz estará apenas a uma distância de x - vt de você. Isso faz δt = vt/c. O semi-período percebido do PHT do relógio de luz é, portanto, dado pela fórmula um tanto complicada na parte inferior direita do diagrama acima. Isso mostra que o semi-período percebido do relógio de luz é um pouco menor do que o semi-período dilatado normal.
Agora, suponha que, em vez de vir em sua direção, o relógio da luz recua de você na velocidade v. Neste caso, o termo v/c deve ser adicionado em vez de subtrair. Consequentemente, o semi-período percebido do PHT do relógio de luz será um pouco mais do que o semi-período dilatado normal. Portanto, o relógio parece estar funcionando ainda mais devagar.
Para um observador em qualquer lugar no plano horizontal que corta o diagrama ao meio, δt = (v/c)cos(θ), onde θ é o rolamento do observador do relógio com referência ao direção em que o relógio está viajando. Então, em geral, o semi-período percebido do relógio de luz transversal é dado por:
O diagrama está olhando para baixo no plano horizontal mencionado acima. Você, portanto, vê apenas o topo do espelho superior. O outro espelho está embaixo dele e, portanto, está totalmente eclipsado por ele. Sempre que o observador não estiver em linha direta com o direção em que o relógio está viajando, θ muda à medida que o relógio se move em relação ao observador. O período do relógio, do ponto de vista do observador, sofre um tipo de efeito Döppler, à medida que o relógio se aproxima do observador, passa e depois afasta-se.
Agora, eu considerarei como o observador percebe o período de um relógio em linha que se move para o observador com a velocidade v, que é uma fração significativa da velocidade da luz.
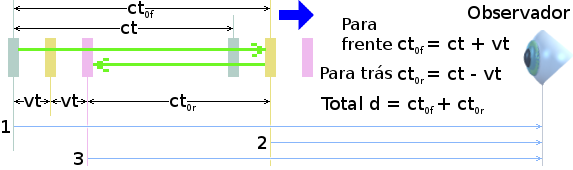
O flash de sinalização 1 do espelho atrás viaja em direção ao observador, juntamente com o próprio flash de temporização interno do relógio. Quando o próprio flash de temporização interno do relógio atinge o espelho da frente, ele aciona o segundo flash de sinalização 2 para marcar o final do primeiro semi-período. Este segundo flash de sinalização corre lado ao lado com o primeiro flash de sinalização até chegarem ao observador. Assim, eles chegam ao observador juntos. O observador, portanto, percebe que o primeiro semi-período do relógio é de duração zero.
Quando ocorre o segundo flash de sinalização, o próprio flash de temporização interno do relógio inicia sua jornada de comprimento ct - vt de volta ao espelho de trás. Lá, ele dispara o terceiro flash de sinalização 3. Isso viaja mais um ct - vt para retornar para onde os dois primeiros flashes de sinalização começaram o lado ao lado em direção ao observador. Assim, este terceiro flash de sinalização está seguindo os dois primeiros flashes 2t(1 - v/c) segundos atrás deles. Esse atraso é o que o observador percebe ser a duração do segundo semi-período do relógio.
Assim, o observador percebe o relógio longitudinal como oscilando um pouco mais rápido do que se fosse estacionário. Se o relógio aproximasse o observador à velocidade da luz, seu período seria zero. Isso passaria a ser infinitamente rápido
O que acontece se o relógio-de-luz longitudinal estiver recuando do observador em vez de aproximar-se?
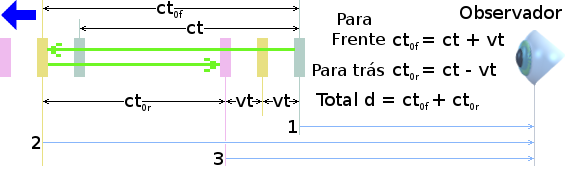
O primeiro flash de sinalização 1 do espelho atrás viaja em direção ao observador como antes, mas o flash de temporização interno do relógio desloca-se coincidentemente para longe do observador. Quando o próprio flash de temporização interno do relógio atinge o espelhod a frente, ele aciona o segundo flash de sinalização 2 para marcar o final do primeiro semi-período. Este segundo flash de sinalização corre lado ao lado com o flash de temporização interno do relógio para uma distância de ct - vt de volta ao espelho de trás. Ao chegar no espelho de trás, o flash de temporização interno do relógio dispara o terceiro flash de sinalização.
A segunda e a terceira flashes de sinalização assim agora correm lado ao lado em direção ao observador. No entanto, esses dois flashes de sinalização devem continuar uma distância adicional de 2vt para chegar ao ponto onde o espelho de trás foi quando o primeiro flash de sinalização o deixou em sua jornada em direção ao observador. Os segunda e terceira flashes de sinalização estão, portanto,correndo lado ao lado a uma distância de (ct + vt) + (ct - vt) + 2vt = 2(ct + vt) atrás do primeiro flash de sinalização.
Os segundo e terceiro flashes de sinalização, assim, chegam juntos ao observador em 2t(1 + v/c) segundos atrás do primeiro flash de sinalização. Esta é a duração percebida pelo observador do primeiro semi-período do relógio de luz recuando. Por que o segundo e o terceiro flashes de sinalização chegam juntos, o segundo semi-período do relógio de luz é percebido ter zero duração.
Assim, contrariamente ao caso do relógio longitudinal que se aproxima, o observador percebe que o relógio longitudinal recuando está correndo um pouco mais lento do que se fosse estacionário. Se o relógio devesse se afastar do observador à velocidade da luz, seu período seria infinito. Seria percebido pelo observador para ser parado.
No caso geral, no qual o observador pode estar em qualquer ângulo θ à progressão do relógio dentro do plano horizontal que corta o diagrama acima ao meio, o período total do relógio varia entre 2t(1 - v/c). A tabela a seguir resume a estrutura do período do relógio para os três modos de viagem em relação ao observador.
| Direcão | 1º Semi-Período | 2º Semi-Período | Período Total |
|---|---|---|---|
| Aproximando | 0 | 2t(1 - v/c) | 2t{1 - (v/c)cos( 0 )} |
| Passando | t(1 + v/c) | t(1 - v/c) | 2t{1 - (v/c)cos(½π)} |
| Recuando | 2t(1 + v/c) | 0 | 2t{1 - (v/c)cos( π )} |
Assim, em geral, o período completo do relógio de luz longitudinal é 2t{1 - (v/c)cos(θ)}. No entanto,isso envolve mais do que simplesmente a variação no período total. Como mostra a tabela acima, a relação entre os dois semi-períodos também varia com θ. O comprimento de cada semi-período sobre todos os valores de θ no plano horizontal parece ser uma função matemática bastante desordenada, o que não posso ser incomodado resolver no momento.
O comportamento do relógio de luz parece ser excessivamente complicado. Sua dependência na velocidade e orientação do relógio em relação ao observador parece estranha, pois, em todas essas experimentos de pensamento, o observador é essencialmente passivo. O observador não participa ativamente no funcionamento do relógio de luz. O observador não é, em qualquer jeito, um componente do mecanismo do relógio de luz.
Eu penso que o motivo dessa complicação é que as experimentos de pensamento acima não consideram a situação corretamente. O processo precisa ser dividido e considerado como dois mecanismos separados operando em série:
O relógio de luz e o espaço intervindo, juntamente com o observador, formam o sistema completo em consideração, que é ilustrado abaixo.
O relógio de luz é um fenômeno, que se comporta de uma certa maneira. Mantém um tempo estável com um período de 2t, que compreende dois semi-períodos, cada um de duração t. O espaço interveniente, entre o relógio e o observador, modifica (ou distorce) a aparência do comportamento do relógio para o observador.
Suponha que eu substituo o relógio de luz no diagrama acima com o relógio mecânico na torre do relógio de Kramgasse, que Einstein observou.
Tente como eu poderia, não consigo ver como um ato de observação, por um observador passivo distante, pode afetar o comportamento do pêndulo ou roda giratória de um relógio mecânico. Conseqüentemente, eu só posso me atribuir todos os efeitos relativistas observados ao espaço interveniente que me separa, o observador, do relógio.
Isto foi tudo o que estava envolvido na suposta situação em que Einstein observou o relógio mecânico na torre em Kramgasse enquanto ele estava se afastando dele no bonde a uma velocidade imaginada que era uma fração significativa da velocidade da luz. Não há nada aqui até agora que tenha envolvido quaisquer noções fantásticas como a dilatação do tempo ou a contração do espaço.
Dentro de seu próprio quadro de referência, o relógio de luz deve manter o tempo exatamente como um relógio mecânico faria. Por isso, estou curioso para saber por que, quando visto por um observador que está em um quadro de referência diferente, o relógio de luz substituído deve exibir um comportamento tão diferente em princípio do relógio mecânico que o substituiu. Eu não acho que ele se comporte de forma diferente. Eu penso que há um erro conceitual na visão estabelecida.
Os primeiros relativistas concluíram corretamente que, para que as leis da física sejam as mesmas para todos os observadores, a velocidade da luz, c, deve parecer a mesma para todos. Mas, sob um regime relativístico, isso exigia que o espaço e o tempo de uma fonte de alguma forma se tornassem, separada e diferentemente, contraídos e dilatados do ponto de vista de cada observador. Não obstante, a geometria dessa postulação não é apenas contra-intuitiva: é claramente paradoxal.
Mas há uma alternativa. Isso envolve simplesmente a mudança da natureza conceitual do éter [luminífero] para o tipo que propus nos 9 ensaios anteriores. Então, um mecanismo para o comportamento da luz pode ser prontamente construído, o que é intuitivo e não paradoxal.
Em vez de ser um dado universal fixo, o éter é reconcebido como um campo de velocidade fluindo radialmente em três dimensões das extremidades do espaço para cada partícula fundamental. Um observador compreende partículas fundamentais. A luz é percebida como uma inscrição, que é gravada por sua fonte neste campo de velocidade à medida que ela passa. O fluxo æthereal convergente então transmite a inscrição gravada para o observador na velocidade da luz, c.
