Classically, it was assumed that light must travel as a progressive disturbance within a fluid medium in a way similar to the way sound waves travel through air. They called this medium the luminiferous æther. It would necessarily have to permeate all space — including the space between the atoms of transparent materials.
The key problem raised by the luminiferous æther was that it would become a fixed universal frame of reference to which the speed of light must be tied. All celestial bodies would move relative to this æther. Consequently, the speed at which light travelled between celestial objects would vary according to the speed and direction of the objects. Furthermore, the motion of all celestial bodies through the æther would produce a drag and a bow wave — just like a ship does when steaming across the ocean. Experimental observation, however, showed that the speed of light did not vary with direction and that it seemed to be independent of the motion of its sources and its observers.
It was therefore postulated that light moved at a universally fixed speed relative to each and every observer. This universal speed of light is usually denoted by the letter c. Light emitted by a single source would thus embark on its journey at speed c away from the source. It would then approach its destination (observer) at the same universal velocity c, no matter at what speed the destination (observer) were travelling relative to the source. The only way to reconcile the geometry of this relationship was to postulate that the source's space became contracted and its time became dilated from the point of view of the observer.

Einstein's Thought Experiment
I think Einstein was riding in a tram (or a trolley bus) along Kramgasse in Bern, Switzerland. He gazed back at the famous clock tower receding from him. Then he thought about how the time on the clock would appear to him if his tram were travelling away from the clock at a significant fraction of the speed of light.
The further he would get away from the clock, the longer the light from the clock face would take to reach him. The effect of this accumulating delay would be to make the clock appear to be running slower than normal. If he had a pocket watch, he would see the hands of the tower clock lagging further and further behind the hands of his pocket watch.
The sole reason the tower clock appears to be running slow is that light does not travel from its clock face to Einstein's eyes instantaneously. It travels at a finite speed and therefore takes a finite time to arrive. When the clock hands move, the light from the clock face takes an ever-increasing amount of time to intimate the new position of the clock hands to Einstein. In other words, it is solely because light travels at a finite speed. It is definitely NOT because the clock is really running slow.
From the point of view of somebody standing in front of the clock tower, its clock is running at normal speed. From the point of view of an observer standing a light-year away from the clock tower but whose speed relative to the clock tower is zero, the clock is running at normal speed. The time this observer sees the clock as indicating will, however, be one year behind what the hands of the clock are currently showing to the observer standing directly in front of it.
However slow the tower clock may appear to be running from the point of view of Einstein on his super-fast tram, the clock of itself, from the point of view of "stationary" observers wherever they may be, is running at normal speed. Einstein's observation of the tower clock from his high-speed vantage point does not therefore modify in any way time, space or motion in the vicinity of the tower clock. There is nothing weird or mind-bending about all this so far.
Things only start to get weird when we examine the difference between the meanings of the words "appears" and "is" in the context of Einstein travelling in his super fast tram away from the Kramgasse clock tower. This is because the speed of light is not only the speed at which the current positions of the clock hands is communicated to Einstein in his super fast tram. It is, more profoundly, the speed at which all physical effects are propagated to Einstein as he is travelling in his super fast tram.
We are well aware that things are often not as they appear, especially in the realm of human relationships. Here, however, we need to stick to purely physical phenomena. A physical example of something not being as it appears is a mirage. One intuitively knows that camels do not usually walk upside down in a bright blue lake. It is an optical illusion caused by a higher than normal temperature gradient in the air close to the ground. In other words, the medium through which the light is travelling from the camels to the observer is modifying the appearance of the scene. The reality is that the camels themselves are walking upright across the sand.
Einstein's observation that the clock on the Kramgasse tower is running slow is not a mirage in the normal sense. It is fundamentally different. This is because the properties of space do not only fix the velocity at which light can travel. They make this same velocity the limit at which anything can travel. For instance, if the clock tower were a planet and it suddenly ceased to exist, its gravitational effect upon Einstein would only cease when it visibly disappeared. This would happen only after the period required for light to travel from the planet to Einstein. For Einstein, it is as if all reality is a mirage. Consequently, from Einstein's point of view, what he sees is reality. In Einstein's universe, the clock on the tower in Kramgasse is running slowly.
It is important to realise that the converse situation is also true. In the universe of an observer standing in front of the clock tower in Kramgasse, the tower clock is running at normal speed and it is Einstein's pocket watch that is running slow. The dilation of time is something which occurs for any observer of any clock that is moving towards or away from him at any speed.
The famous thought experiment, involving a light-clock, was constructed to illustrate how this was supposed to happen. In the diagram below, the grey rectangles represent a pair of mirrors. The mirrors face each other. They are mounted on a common frame so they always remain the same fixed distance apart.
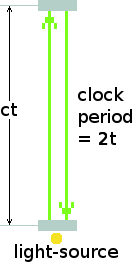 In the middle of one of the mirrors is a small hole through which shines a perfectly collimated light source such as a perfect laser. The light-source emits an initial flash of light. The light travels to the upper mirror. There it is reflected back to the lower mirror, which then reflects it back again to the upper mirror. Thus the light continues forever to reflect back and forth between the two mirrors. The light travels on its path between the two mirrors at velocity c. The period of the clock is defined as the time it takes the flash of light to make the round trip from the lower mirror to the upper mirror and back again. This is twice the time t that the light takes to travel one leg between one mirror and the other. The period of the light-clock is therefore 2t. Consequently, the distance the light travels during one clock-period is 2ct.
In the middle of one of the mirrors is a small hole through which shines a perfectly collimated light source such as a perfect laser. The light-source emits an initial flash of light. The light travels to the upper mirror. There it is reflected back to the lower mirror, which then reflects it back again to the upper mirror. Thus the light continues forever to reflect back and forth between the two mirrors. The light travels on its path between the two mirrors at velocity c. The period of the clock is defined as the time it takes the flash of light to make the round trip from the lower mirror to the upper mirror and back again. This is twice the time t that the light takes to travel one leg between one mirror and the other. The period of the light-clock is therefore 2t. Consequently, the distance the light travels during one clock-period is 2ct.
To make use of such a clock, it would be necessary to monitor its ticks. This requires the intervention of some kind of detector to determine each instant when the light hits the lower mirror. In the real world, this would sap energy from the flash of light, so it would gradually fade out. There would have to be some means of causing a fading flash to trigger a new flash. Notwithstanding, this is only a thought experiment, so our detector can be imaginary. And an imaginary detector does not consume energy.
Moving Light-Clock
The next stage of this thought experiment is to consider what happens if the clock is moving relative to an observer at a speed v, which is a significant proportion of the speed of light.
In the traditional version of this thought experiment, the observer is looking straight at the screen or page, as you are now doing, and the clock assembly is moving across the page from left to right. However, the same geometry would hold for an observer placed at the left or right sides of the diagram, or indeed anywhere on the horizontal plane that would cut the diagram in half. This is because I am considering only what is happening within the clock itself and not how information about the clock's current state is conveyed to the observer.
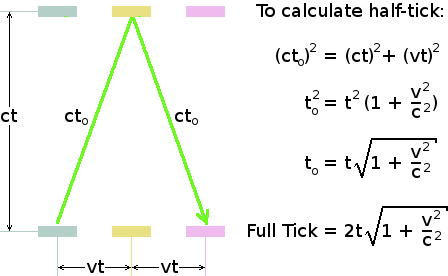
In the time t taken by the light to travel from one mirror to the other, the clock assembly moves a distance vt to the right. From the clock's point of view, the light simply travels a distance ct straight from one mirror to the other. However, from the observer's point of view, the opposite mirror has moved a distance vt to the right in this time. In the observer's frame of reference, the light therefore has to travel a distance ct0 in order to arrive at the opposite mirror.
The calculation of the light-clock's period from the point of view of the observer is a simple application of Pythagoras's Theorem to the right-angled triangle of which the distance ct0 is the hypotenuse. The formula for the full period or full-tick of the clock, from the point of view of the observer, is shown at the bottom right of the above diagram. It is somewhat longer than 2t, the clock's period from the point of view of the clock itself. From the observer's point of view, the clock is therefore running much slower.
Traditionally, the purpose of the above thought experiment was not to show that a "moving" light-clock runs slow within the frame of reference of a "stationary" observer. It's purpose was to show that if the speed of light always be the same in all frames of reference, then the time in the "moving" frame of reference is always dilated with respect to the observer's "stationary" frame of reference.
However, for the purpose of this essay, I wish to continue considering the way the light-clock itself behaves in different situations.
Rotated Light-Clock
Suppose I rotate the light-clock assembly through a right-angle, that is, a quarter-turn or 90° as shown below.
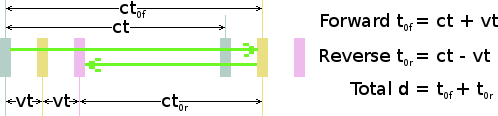
The geometry shows that, although the clock assembly is still travelling from left to right at velocity v, at a significant fraction of the speed of light, the time dilation changes with the direction of the light. On the forward stretch, the light travels a distance of ct0f = ct + vt in time t(1 + v/c), whereas on the reverse stretch it travels a distance of ct0r = ct - vt in time t(1 - v/c). The full light-path in the observer's space d = ct0f + ct0r = ct + vt + ct - vt, which is simply 2ct.
The clock's full period is therefore 2t, the same as if the clock were stationary. So the in-line light-clock, from the point of view of the observer, runs at normal speed. A summary of the distances and durations of the light's journeys between the mirrors is shown in the following table.
| Period
| Distance
| Duration
|
| 1st Half-period
| ct + vt
| t(1 + v/c)
|
| 2nd Half-period
| ct − vt
| t(1 − v/c)
|
| Full Period
| ct + vt + ct − vt = 2ct
| 2t
|
The tick of the transverse light-clock is symmetrical. Each half-period is of the same duration. The in-line light-clock does not, however, tick symmetrically. The first half of its tick is longer than the second half. It seems strange that time should dilate by two different amounts over the clock's cycle, while the relative velocity between the clock and the observer remains constant.
Two Clocks in a Spaceship
Suppose two identical light-clocks are installed in a spaceship. One is mounted transversely, i.e. across a diameter of the spaceship. The other is mounted longitudinally, i.e. in line with the axis of the space-ship.
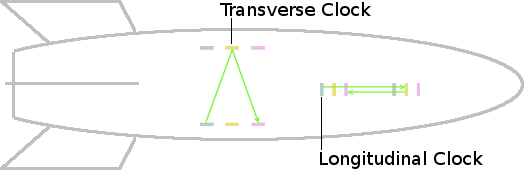
The spaceship takes off from Earth and maintains a course directly away from the Earth. To an observer on Earth, the transverse clock is running slow and the longitudinal clock is running at normal speed.
This implies that, in the observer's frame of reference, while time is running at normal speed along the line of the spaceship's route, it is running slowly within the plane perpendicular to the line of the route. This situation will be exactly the same when the spaceship returns. Time in line with the route will always pass normally, while time within the diametric plane of the spaceship will, again, always pass more slowly.
The Twins Paradox
What consequences does this have for the biological clocks of the crew of the spaceship? How will the crew age during a round trip to a nearby star and back at a significant fraction of the speed of light? Neglecting gravitational effects for the moment, all aspects of their biology that are in line with the Earth will age at the normal rate as on Earth. Aspects of their biology that are in any other orientation will age progressively more slowly as their orientation gets closer to the diametric plane of the spaceship.
In other words, each crew member will age vertically more slowly than he ages horizontally. If a crew member has a twin who remained on Earth during the voyage, then his twin will see his brother to be younger than he only in the vertical direction. This effect is not simply at a macroscopic scale. It penetrates right down to the ultimate granularity of space. Each atom — nay, each "string" — must "tick" more slowly in one dimension than in the other two, which is clearly a physical absurdity.
If the two light-clocks run at different speeds according to their orientation to the direction of motion, at what speed must a mechanical spin-wheel clock run? If its spin-wheel's axis is in the diametric plane of the spaceship, will it run slower than if its spin-wheel is in line with the spaceship's axis? I think not.
As Perceived by A Human Observer
 In the previous thought experiment, the observer cannot have been human. He must have been some kind of omnipotent being. This is because, for the observer to have observed the speed of the light-clock in each case, he would have had to be able to observe all points in space at each instant. I did not consider how information about the clock's current state at any given time would get from the travelling light-clock to a normal human observer in real space.
In the previous thought experiment, the observer cannot have been human. He must have been some kind of omnipotent being. This is because, for the observer to have observed the speed of the light-clock in each case, he would have had to be able to observe all points in space at each instant. I did not consider how information about the clock's current state at any given time would get from the travelling light-clock to a normal human observer in real space.
Transverse Clock as Observed
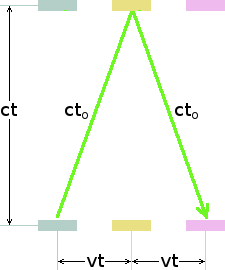 You, a human observer, observe the transverse version of the light-clock passing across your field of view from left to right at a velocity v, which is a significant fraction of the speed of light. A light-detector is attached to each mirror. This triggers a separate light-source, which sends a short flash in your direction every time the clock's own timing flash hits the mirror to which it is attached. You therefore see a flash of light alternately from each mirror. You therefore see a flash for every half-period of the light-clock. But the flashes you see do not arrive the instant they are emitted by the flasher on the mirror concerned. They require a time T to traverse the space between you and the clock.
You, a human observer, observe the transverse version of the light-clock passing across your field of view from left to right at a velocity v, which is a significant fraction of the speed of light. A light-detector is attached to each mirror. This triggers a separate light-source, which sends a short flash in your direction every time the clock's own timing flash hits the mirror to which it is attached. You therefore see a flash of light alternately from each mirror. You therefore see a flash for every half-period of the light-clock. But the flashes you see do not arrive the instant they are emitted by the flasher on the mirror concerned. They require a time T to traverse the space between you and the clock.
The two mirrors continue at a constant distance from you as they traverse your field of view from left to right. The time T for each flash to arrive will therefore be constant. You will therefore see this clock running at the slow rate previously calculated. But suppose you observe the clock coming directly towards you at velocity v. What will the clock's period be then, from your point of view?
As shown in the following diagram, the dilated half-tick t0 of the travelling light-clock is the same. However, the flash you see from the bottom mirror will take longer to reach you than will the flash from the top mirror when it occurs. This is because, by the time the flash from the top mirror occurs, the clock will have moved a distance vt closer to you. The flash from the top mirror will appear to you to occur a little sooner δt than it should do. You will therefore perceive the clock's half-tick to be only t0 - δt.
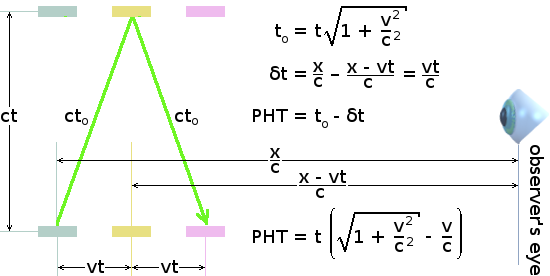
If the light-clock is a distance x from you when the first flash from the bottom mirror occurs, then when the flash occurs from the top mirror after the first half-tick, the light-clock will be only at a distance of x - vt from you. This makes δt = vt/c. The perceived half-tick of the light-clock PHT is therefore given by the somewhat complicated formula at the bottom right of the above diagram. This shows the perceived half-period of the light-clock to be somewhat less than the normal dilated half-period.
Now suppose that, instead of coming towards you, the light-clock is receding from you at velocity v. In this case, the v/c term must be added instead of subtracted. Consequently, the perceived half-period of the light-clock PHT will be somewhat more than the normal dilated half-period. So the clock will appear to be running even slower.
For an observer anywhere on the horizontal plane that cuts the diagram in half, δt = (v/c)cosθ, where θ is the bearing of the observer from the clock with reference to the clock's heading. So, in general, the perceived half-tick of the transverse light-clock is given by:

The diagram is looking down on the horizontal plane mentioned above. You therefore only see the top of the top mirror. The other mirror is underneath it and is therefore fully eclipsed by it. Whenever the observer is not in direct line with the clock's heading, θ changes as the clock moves relative to the observer. The clock's tick, from the observer's point of view, thus suffers a kind of Doppler effect as the clock approaches him, passes him and then recedes from him.
Now I shall consider how the observer perceives the tick of an in-line clock moving towards him with velocity v, which is a significant fraction of the speed of light.

The signalling flash 1 from the rear mirror travels towards the observer together with the clock's own internal timing flash. When the clock's own internal timing flash hits the forward mirror, it triggers the second signalling flash 2 to mark the end of the first half-tick. This second signalling flash then runs neck and neck with the first signalling flash until they reach the observer. Thus they arrive at the observer together. The observer therefore perceives the first half-period of the clock to be of zero duration.
When the second signalling flash occurs, the clock's own internal timing flash starts its journey of length ct − vt back to the rear mirror. There it triggers the third signalling flash 3. This then travels a further ct − vt to get back to where the first two signalling flashes started their neck and neck run towards the observer. Thus this third signalling flash is following the first two 2t(1 - v/c) seconds behind them. This delay is what the observer perceives to be the duration of the second half-period of the clock.
The observer thus perceives the in-line clock to be ticking somewhat faster than if it were stationary. If the clock were to approach the observer at the speed of light, its period would be zero. It would be ticking infinitely fast.
What happens if the in-line light-clock is receding from the observer instead of approaching?

The first signalling flash 1 from the rear mirror travels towards the observer as before but the clock's internal timing flash coincidently travels away from the observer. When the clock's own internal timing flash hits the forward mirror, it triggers the second signalling flash 2 to mark the end of the first half-tick. This second signalling flash then runs neck and neck with the clock's internal timing flash for a distance of ct - vt back to the rear mirror. On arriving at the rear mirror, the clock's internal timing flash triggers the third signalling flash.
The second and third signalling flashes thus now run neck and neck towards the observer. However, these two signalling flashes must continue a further distance of 2vt to arrive at the point where the rear mirror was when the first signalling flash left it on its journey towards the observer. The second and third signalling flashes are thus travelling neck and neck at a distance of (ct + vt) + (ct - vt) + 2vt = 2(ct + vt) behind the first signalling flash.
The second and third signalling flashes thus arrive together at the observer 2t(1 + v/c) seconds behind the first signalling flash. This is the observer's perceived duration of the first half-period of the receding light-clock. Since the second and third signalling flashes arrive together, the perceived second half-period of the receding light-clock is of zero duration.
Thus, contrary to the case of the approaching in-line clock, the observer perceives the receding in-line clock to be ticking somewhat slower than if it were stationary. If the clock were to recede from the observer at the speed of light, its period would be infinite. It would be perceived by the observer to be stopped.
In the general case, where the observer can be at any angle θ to the clock's motion within the horizontal plane that cuts the above diagram in half, the total period of the clock varies between 2t(1 - v/c) and 2t(1 + v/c). The following table summarizes the structure of the clock's period for its three modes of travel with respect to the observer.
| Direction
| 1st Half-Period
| 2nd Half-Period
| Full Period
|
| Approaching
| 0
| 2t(1 − v/c)
| 2t{1 − (v/c)cos( 0 )}
|
| Traversing
| t(1 + v/c)
| t(1 − v/c)
| 2t{1 − (v/c)cos(½π)}
|
| Receding
| 2t(1 + v/c)
| 0
| 2t{1 − (v/c)cos( π )}
|
Thus, in general, the full period of the in-line light-clock is 2t{1 - (v/c)cos(θ)}. There is more to it, however, than the simple variation in the total period. As the above table shows, the distribution of the full period between the two half periods also varies with θ. The length of each half-period over all values of θ in the horizontal plane seems to be quite a messy mathematical function, which I can't be bothered to work out at the moment.
Two Separate Considerations
The behaviour of the light-clock seems to be overly complicated. Its dependence on the clock's velocity and orientation relative to the observer seems strange, since, in all these thought experiments, the observer is essentially passive. He does not actively participate in the operation of the light-clock. He is in no sense a component of the light-clock's mechanism.
I think the reason for this complication is that the above thought experiments fail to consider the situation correctly. The process needs to be broken down and considered as two separate mechanisms operating in series:
- the light-clock itself (the phenomenon being observed) and
- the intervening space between the light-clock and the observer
(the information delivery mechanism).
The light-clock and the intervening space, together with the observer, form the complete system under consideration, which is illustrated below.
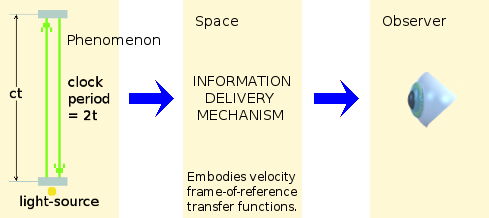
The light-clock is a phenomenon, which behaves in a certain way. It keeps steady time with a period of 2t, comprising two half-periods each of duration t. The intervening space, between the clock and the observer, modifies (or distorts) the appearance of the clock's behaviour to the observer.
Suppose I replace the light-clock in the above diagram with the mechanical clock in the Kramgasse clock tower, which Einstein observed.
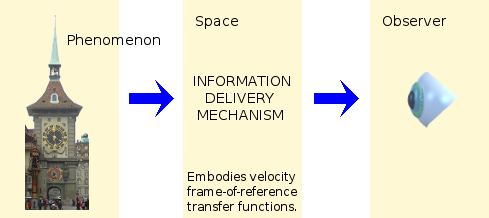
Try as I might, I cannot see how an act of observation, by a distant passive observer, can possibly affect the behaviour of the pendulum or spin-wheel of a mechanical clock. Consequently, I can only bring myself to attribute all the observed relativistic effects to the intervening space that separates me, the observer, from the clock.
This is all that was involved in the purported situation in which Einstein observed the mechanical clock in the tower in Kramgasse as he was receding from it on the tram at an imagined velocity that was a significant fraction of the speed of light. There is nothing here so far that has to involve any fanciful notions like dilated time or contracted length.
Within its own frame of reference, the light-clock should keep time exactly as a mechanical clock would do. I am therefore curious to know why, when viewed by an observer who is in a different frame of reference, the replaced light-clock should exhibit a behaviour so different in principle from that of the mechanical clock which replaced it. I don't think it does behave differently. I think there is a conceptual error in the established view.
An Alternative Hypothesis
Early relativists rightly concluded that, in order for the laws of physics to be the same for all observers, the velocity of light, c, must appear the same to all. But, under a relativistic regime, this required that a source's space and time somehow had to become, separately and differently, contracted and dilated from the point of view of each observer. Notwithstanding, the geometry of this postulation is not just counter-intuitive: it is plainly paradoxical.
But there is an alternative. This simply involves changing the conceptual nature of the [luminiferous] æther to the kind I have hypothesised in the previous 9 essays. Then a mechanism for the behaviour of light can be readily constructed, which is at once both intuitive and non-paradoxical.
Instead of being a fixed universal datum, the æther is re-conceived as a velocity-field flowing radially in three dimensions from the extremities of space into each fundamental particle. An observer comprises fundamental particles. Light is perceived as an inscription, which is etched by its source up on this velocity field as it passes by. The converging æthereal flux then conveys the etched inscription to the observer at the velocity of light, c.
© 11-19 June 2013 Robert John Morton |
NEXT


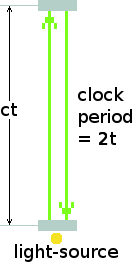 In the middle of one of the mirrors is a small hole through which shines a perfectly collimated light source such as a perfect laser. The light-source emits an initial flash of light. The light travels to the upper mirror. There it is reflected back to the lower mirror, which then reflects it back again to the upper mirror. Thus the light continues forever to reflect back and forth between the two mirrors. The light travels on its path between the two mirrors at velocity c. The period of the clock is defined as the time it takes the flash of light to make the round trip from the lower mirror to the upper mirror and back again. This is twice the time t that the light takes to travel one leg between one mirror and the other. The period of the light-clock is therefore 2t. Consequently, the distance the light travels during one clock-period is 2ct.
In the middle of one of the mirrors is a small hole through which shines a perfectly collimated light source such as a perfect laser. The light-source emits an initial flash of light. The light travels to the upper mirror. There it is reflected back to the lower mirror, which then reflects it back again to the upper mirror. Thus the light continues forever to reflect back and forth between the two mirrors. The light travels on its path between the two mirrors at velocity c. The period of the clock is defined as the time it takes the flash of light to make the round trip from the lower mirror to the upper mirror and back again. This is twice the time t that the light takes to travel one leg between one mirror and the other. The period of the light-clock is therefore 2t. Consequently, the distance the light travels during one clock-period is 2ct.



 In the previous thought experiment, the observer cannot have been human. He must have been some kind of omnipotent being. This is because, for the observer to have observed the speed of the light-clock in each case, he would have had to be able to observe all points in space at each instant. I did not consider how information about the clock's current state at any given time would get from the travelling light-clock to a normal human observer in real space.
In the previous thought experiment, the observer cannot have been human. He must have been some kind of omnipotent being. This is because, for the observer to have observed the speed of the light-clock in each case, he would have had to be able to observe all points in space at each instant. I did not consider how information about the clock's current state at any given time would get from the travelling light-clock to a normal human observer in real space.
 You, a human observer, observe the transverse version of the light-clock passing across your field of view from left to right at a velocity v, which is a significant fraction of the speed of light. A light-detector is attached to each mirror. This triggers a separate light-source, which sends a short flash in your direction every time the clock's own timing flash hits the mirror to which it is attached. You therefore see a flash of light alternately from each mirror. You therefore see a flash for every half-period of the light-clock. But the flashes you see do not arrive the instant they are emitted by the flasher on the mirror concerned. They require a time T to traverse the space between you and the clock.
You, a human observer, observe the transverse version of the light-clock passing across your field of view from left to right at a velocity v, which is a significant fraction of the speed of light. A light-detector is attached to each mirror. This triggers a separate light-source, which sends a short flash in your direction every time the clock's own timing flash hits the mirror to which it is attached. You therefore see a flash of light alternately from each mirror. You therefore see a flash for every half-period of the light-clock. But the flashes you see do not arrive the instant they are emitted by the flasher on the mirror concerned. They require a time T to traverse the space between you and the clock.





