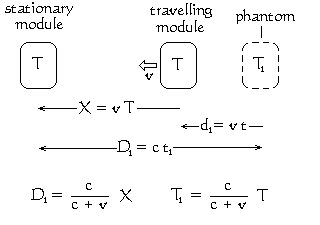In the nine essays about the universe [see panel on the left] I endeavoured to establish an alternative model for light as an inscription etched by the source onto an ætherial flux that continually converges towards the observer at velocity c. This mandates that the velocity of light c be tied exclusively to the frame of reference of the observer. So now herein I discuss the passage of light, from a source to an observer, from the point of view of the observer's frame of reference.
We must be extremely careful not to subconsciously think of the piece of paper or browser window, upon or within which the following diagram appears, as a frame of reference. It is easy to look at the diagram and think of the position of the phantom — the place where the observed was when it emitted the light — as "stationary".
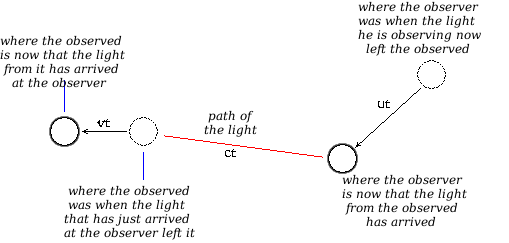
But "stationary" relative to what? The whole page (or browser window) could be "moving". We can avoid this relative velocity problem as follows. Consider the instant at which one "photon" of light is emitted from the observed. This "instant" occupies an infinitessimally small duration of time δt. Consequently all motion in the universe is effectively "frozen" during this period. At this instant, the observed occupies a definite position in space and time.
Time then continues and the "photon" moves away from its starting point. As far as the "photon" is concerned, the future motion of the observed is irrelevant. It plays no further significant role in determining the path or destiny of the "photon". During the "photon's" journey, the observer — its final destination — also is irrelevant. Neither the observed nor the observer influence or affect it in any significant way. Eventually, during another infinitessimally small period of time δt, the photon hits an atom in the observer's eye, contributing to the observer's overall vision of the observed.
Whether or not the observer is moving relative to the point of origin of the photon is irrelevant. It does not affect the fact that when the photon is absorbed, it has travelled a definite distance and has taken a definite time to do it. Dividing this definite distance by this definite time yields a natural constant called the velocity of light. However, this "velocity" does not only apply to light. It is also the maximum "velocity" at which all influences can be conveyed from one place to another. It is the maximum "velocity" at which information can be propagated.
The fundamental consequence of this maximum "velocity" for information transfer is that an observer can only see — and can only be affected by — past events. Conversely, an observed can only be seen by — and can only have an effect on — an observer in the future. What one does "now" can only ever affect others "later". This is not merely a limitation of human scale and physique: it is a fundamental limitation built into the very fabric of existence. This leads to a further consequence.
The reality, within which any given observer exists, can only ever be a small part of what is. His reality comprises only that part of all reality that lies within a "solid" sphere of space-time that is unique to him, at the centre of which he resides. The radius of this sphere extends both away from his present position in space and backwards from his present position in time.
Points equidistant from him in different directions can themselves be separated by large distances. And though equidistant into his past, these equidistant points can themselves occupy vastly different positions in time relative to each other. Going backwards into the past in one direction is not the same as going backwards into the past in another direction. Thus time itself, like distance, must necessarily also be a vector quantity. From the point of view of the observer, therefore, only direct radial distances, within his sphere of observation, are relevant or real.
He can, at any given instant, see — or otherwise be independently affected by — events within this sphere. It is his only, exclusive and unique observable universe. It is his only and unique reality. But it is a universe, or reality, that he is fundamentally unable to influence or change. He cannot change or influence the history he can see and experience.
If our observer acts in such a way that results in his 'emitting' light or some other influence, then this light or influence is drawn outwards from him into another sphere of space-time — another universe — about which he knows nothing. He cannot change his own history but he can influence the future 'history' of others.
An Alternative Thought Experiment
Consider a spaceship that comprises 3 equal modules. Each module is cylindrical. The 3 modules are connected in-line to form a cylinder 3 times the length of each individual module. The modules are connected together by quick-release catches.

Between each pair of modules is a strong compressed spring. The catches binding the modules together are released simultaneously. The springs accelerate the two outer modules in opposite directions, away from the central module, in a straight line. They do this with such force that the outer modules end up travelling away from the central module at a relativistically significant fraction of the speed of light, v. They continue on their journey in opposite directions indefinitely.

Each space module has on-board an accurate clock. While the 3 modules were yet connected, in other words, before the spring catches were released, the clocks on the 3 modules were synchronized. They showed exactly the same time.
Let us consider the time shown on the clock on-board one of the departed "travelling" modules compared with the clock on-board the central "stationary" module. The outbound module has been travelling quite some time. Suppose the elapsed time shown on the clock of the "stationary" module is T.
If the time dilation effect of relativity is a real warping of the "fabric" of space-time, then the elapsed time indicated by the clock in the "travelling" module will be less than T. However, to the people on-board the "travelling" module, time seems to pass normally. If this is true, their clock should indicate the same elapsed time, namely T. Let us suppose that both clocks indicate an elapsed time of T. What will the crew of the "stationary" module perceive the clock on the "travelling" module to indicate?
For this exercise, I will take the liberty of making the assumption that information cannot travel faster than the speed of light. If this assumption is ever proved to be incorrect then our argument fails. However, assuming it is true; the crew of the "stationary" module can never observe the actual position of the "travelling" module. Neither can they ever observe the actual time shown on the clock in the "travelling" module. They can only ever see, perceive or by any means acquire information about a past "phantom" of the "travelling" module and its clock.
 This past phantom is how the "travelling" module was at some time t1 in the past. Here, t1 is the time that information takes to travel the distance D1 from the position of the phantom to the "stationary" module. Since the maximum velocity at which information can travel is that of light c, this distance must be given by D1 = c t1. The elapsed time T1 shown on the phantom's clock at elapsed time T on the clock of the "stationary" module must be given by T1 = T − t1.
This past phantom is how the "travelling" module was at some time t1 in the past. Here, t1 is the time that information takes to travel the distance D1 from the position of the phantom to the "stationary" module. Since the maximum velocity at which information can travel is that of light c, this distance must be given by D1 = c t1. The elapsed time T1 shown on the phantom's clock at elapsed time T on the clock of the "stationary" module must be given by T1 = T − t1.
As the "travelling" module moves further and further away from the "stationary" module, the time t1 required for the information to get to the observer on the "stationary" module will forever increase. Consequently, as t1 increases, T − t1 decreases. Hence the clock on-board the phantom — what the observer on the "stationary" module perceives to be the "travelling" module — appears to be running slow. Its seconds are longer than those of the local clock. Furthermore, the phantom is falling further and further behind the actual "travelling" module.
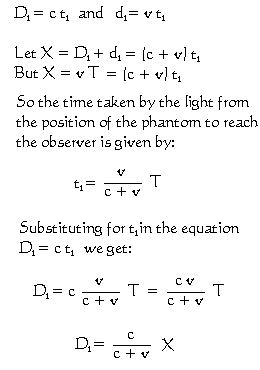 Let us now consider the distance D1 of the phantom from the observer in terms of the distance X of the reality from the observer. Intuition would suggest that, as the reality gets further and further away from the observer, its phantom will lag further and further behind. The adjacent algebra derives a formal expression for D1 in terms of X. This shows that if the velocity v of the "travelling" module is a constant, then D1 will be a constant fraction of X. If the "travelling" module were to travel at the velocity of light, its phantom would travel at half the velocity of light. If the "travelling" module were to travel at a million times the velocity of light, its phantom would travel at only 1,000,000÷1,000,001 times the velocity of light. That is 0·999999000000999999000000999999c. So however fast the reality travels relative to the observer, the observer sees it only as a phantom travelling at less than the velocity of light.
Let us now consider the distance D1 of the phantom from the observer in terms of the distance X of the reality from the observer. Intuition would suggest that, as the reality gets further and further away from the observer, its phantom will lag further and further behind. The adjacent algebra derives a formal expression for D1 in terms of X. This shows that if the velocity v of the "travelling" module is a constant, then D1 will be a constant fraction of X. If the "travelling" module were to travel at the velocity of light, its phantom would travel at half the velocity of light. If the "travelling" module were to travel at a million times the velocity of light, its phantom would travel at only 1,000,000÷1,000,001 times the velocity of light. That is 0·999999000000999999000000999999c. So however fast the reality travels relative to the observer, the observer sees it only as a phantom travelling at less than the velocity of light.
Of course, the algebra is a little more complicated for an observer who is located off the line of trajectory of the "travelling" module. However, the essential principle is the same.
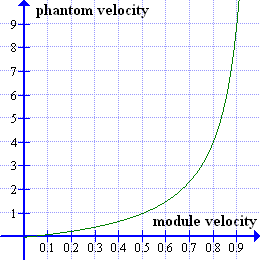
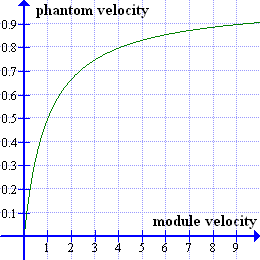 The ratio between the distance X of the "travelling" module and the distance D of the phantom from the observer on the "stationary" module varies inversely with the velocity v of the "travelling" module. Their velocities should also be in this same ratio. The graph on the left uses this ratio to plot the velocity of the phantom against the velocity of the "travelling" module in units of c, the velocity of light. Ignore just for the moment the physical "legality" of the module travelling beyond the speed of light. We see that, however fast the module itself travels, its phantom — what is to the observer the effective physical reality of the module — can never attain the speed of light.
The ratio between the distance X of the "travelling" module and the distance D of the phantom from the observer on the "stationary" module varies inversely with the velocity v of the "travelling" module. Their velocities should also be in this same ratio. The graph on the left uses this ratio to plot the velocity of the phantom against the velocity of the "travelling" module in units of c, the velocity of light. Ignore just for the moment the physical "legality" of the module travelling beyond the speed of light. We see that, however fast the module itself travels, its phantom — what is to the observer the effective physical reality of the module — can never attain the speed of light.
 Now we can derive the time shown by the clock on-board the "travelling" module from the point of view of the observer on-board the "stationary" module....
Now we can derive the time shown by the clock on-board the "travelling" module from the point of view of the observer on-board the "stationary" module....
To the observer on-board the "stationary" module, the phantom of the "travelling" module is not an illusion. It is in every way real. It is not only the position from where the visible image of the "travelling" module originates. It is also the place from where its gravitational influence originates. It is the place of origin of all physical effects of the "travelling" module upon the "stationary" module. It is the "travelling" module's only connection with the "stationary" module's frame of reference. The reality of the "travelling" module itself is effectively outside the "stationary" module's universe.
Motion is relative. Therefore, which module is regarded as "stationary" and which module is regarded as "travelling" is arbitrary. It all depends on which module we currently consider to be the "observer". The "observer" and the "observed" can therefore be freely interchanged without altering the principle of our experiment. Each module can therefore observe — and be affected by — only the phantom of the other. The respective realities of the two modules are fundamentally unable to communicate directly with each other. The reality of each can be observed and affected only by the phantom of the other.
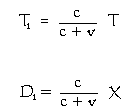 From the above, we have seen that — from the point of view of the observer — the time on-board the "travelling" module dilates by an amount given by the formula...
From the above, we have seen that — from the point of view of the observer — the time on-board the "travelling" module dilates by an amount given by the formula...
We have also seen that — from the point of view of the observer the distance to the "travelling" module contracts by an amount given by the formula...
Furthermore, if, from the point of view of the stationary module, the distance to the travelling module appears to contract, then so too must the physical length of the travelling module itself.
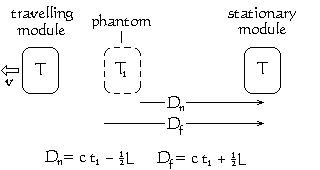 In the diagram on the left, Dn is the distance of the near end of the phantom from the observer's eye on-board the "stationary" module. Correspondingly, Df is the distance of the far end of the phantom. Df is greater than Dn by an amount equal to the length of the phantom image of the "travelling" module. It therefore takes the light a little longer to reach the observer's eye from the far end of the "travelling" module than it does from its near end. This extra time is L/c, where L is the length of the phantom.
In the diagram on the left, Dn is the distance of the near end of the phantom from the observer's eye on-board the "stationary" module. Correspondingly, Df is the distance of the far end of the phantom. Df is greater than Dn by an amount equal to the length of the phantom image of the "travelling" module. It therefore takes the light a little longer to reach the observer's eye from the far end of the "travelling" module than it does from its near end. This extra time is L/c, where L is the length of the phantom.
The observer sees both the far end of the phantom and the near end of the phantom at the same time. The light he sees arriving from the far end of the phantom must therefore have started its journey to him slightly earlier than the light from the near end of the phantom. The light from the far end of the phantom must have left the phantom when the phantom was closer to the observer than it was when the light left the near end of the phantom. Consequently the phantom will appear to be shorter than it really is.
But is this a real contraction of space and dilation of time? To answer this, let us consider the third module that sprung off in the opposite direction. This third module has a velocity relative to the first travelling module that is double that between the "stationary" module and the first "travelling" module. To an observer on-board the second "travelling" module, the phantom of the first "travelling" module will be in a different position.
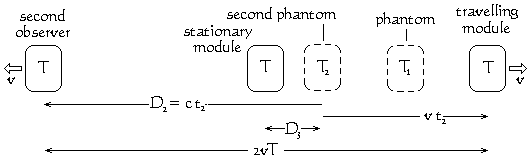
Light from the first "travelling" module takes longer to reach the second "travelling" module than it does to reach the "stationary" module. The phantom of the first "travelling" module seen by the observer on the second "travelling" module will therefore be older than the phantom of the first "travelling" module seen by the observer on the "stationary" module. From the above diagram therefore:
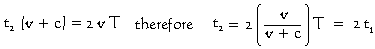
The distance D2 of the second phantom from the second "travelling" module is therefore twice the distance D1 of the first phantom from the "stationary" module. The distance of the second "travelling" module from the "stationary" module is the same as the distance of the first "travelling" module from the "stationary" module, namely X. The distance of the second phantom from the "stationary" module D3 is therefore D2 − X. Hence...
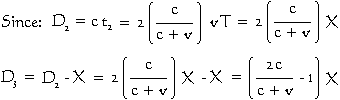
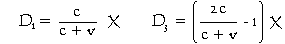 Essentially, D3 is different from D1. This means that two separate phantoms exist and that they occupy different locations in space.
Essentially, D3 is different from D1. This means that two separate phantoms exist and that they occupy different locations in space.
In the following diagram I have put the modules slightly out of line to make the illustration clearer. Although, strictly speaking, this makes the geometry more complicated, it does not alter the principles I am illustrating.

From this diagram we can see that the two observers are observing two different things. Each phantom occupies a different position in space. The two phantoms are also different in age. The "travelling" observer is observing an older phantom than is the "stationary" observer. Consequently, the two phantoms are also at different positions in time. The two phantoms are places where the real observed "travelling" module has already been.
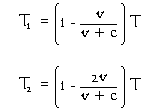 Furthermore, the rate at which time is observed to pass is different for each phantom. The "stationary" observer sees the elapsed time on the clock inside the first phantom as T1 whereas the "travelling" observer sees the elapsed time on the clock inside the second phantom as T2 as shown on the right. The observed "travelling" module is moving away from the "travelling" observer twice as fast as it is from the "stationary" module. Consequently, the clock in the second phantom appears to run at only half the speed of the clock in the first phantom.
Furthermore, the rate at which time is observed to pass is different for each phantom. The "stationary" observer sees the elapsed time on the clock inside the first phantom as T1 whereas the "travelling" observer sees the elapsed time on the clock inside the second phantom as T2 as shown on the right. The observed "travelling" module is moving away from the "travelling" observer twice as fast as it is from the "stationary" module. Consequently, the clock in the second phantom appears to run at only half the speed of the clock in the first phantom.
Remember that each observer's respective phantom is not merely the place from where the light image of the observed "travelling" module originates. It is also the place from which the observer "feels" gravitation and all other physical influences of the observed "travelling" module. Each observer perceives his phantom as the real thing. The real module, to him, doesn't exist. It is beyond his event horizon.
Notwithstanding: in true reality, light and all other physical effects can, fundamentally, be emitted by — come from — only the real module: not its phantom. The phantom's present location is where the real module was when it emitted the light the observer is now receiving.
To each observer, time on-board the observed "travelling" module appears to be dilated to a different extent. However, this does not mean that time itself is actually dilated in the vicinity of the observed "travelling" module. If it were, it would have to be dilated at as many rates as there were observers observing it. If instead of two observer modules we had a million, then the fabric of time within the vicinity of the observed "travelling" module would have to be dilated at a million different concurrent rates. This does not sound plausible.
A much more plausible view is that time merely appears to be dilated differently to each observer. The cause of this apparent dilation must therefore be to do with how information about the observed "travelling" module is conveyed to each respective observer. It can only be to do with how space-time itself conveys information.
What About A Return Journey?
For this, let us replace our 3-module spaceship with a 5-module spaceship. Each module is cylindrical. The 5 modules are connected in-line to form a cylinder 5 times the length of each individual module. The modules are connected together by quick-release catches.

Between each adjacent pair of modules is a strong compressed spring. When the catch binding an adjacent pair of modules is released, the spring accelerates the modules apart in opposite directions in a straight line. The catches binding the central module to its two immediate neighbours are released. The springs accelerate the two bound pairs of modules in opposite directions so that they end up travelling away from the central module at almost the speed of light.

Please note: in the previous 3-module thought experiment, the springs each side of the central module each accelerated only one module to the significant fraction of the speed of light, v. This time however, the springs must be stronger so as to be able to accelerate two modules to the same significant fraction of the speed of light, v.
They continue on their journey in opposite directions. After each module-pair has been travelling for what its respective crew perceives to be 7 years, each crew releases the catch between its pair of modules. The two modules of each pair are forced apart by the compressed spring between them.

The spring between the two modules of each outbound pair is just as strong as the springs that were released 7 years previously between each module-pair and the central module.
This is because, although each spring needs now only to accelerate half the mass, it needs to accelerate its module-pair apart in opposite directions so as to achieve a relative velocity between them of double the 'significant fraction of the speed of light', 2v. This is so that the home-bound module will have a velocity relative to the stationary module of the original 'significant fraction of the speed of light', v.
The outer two modules on each side of the experiment will continue in their same respective directions but now at an increased velocity of 2v away from the central module. They continue to travel apart forever.
Eventually, after a further 7 years, the two modules that are now travelling back towards the central module, from opposite directions, each at a velocity v with respect to the central [stationary] module, re-connect with the central module.

Presumably there is a benign means of killing their vast relative velocities as they meet. Perhaps some kind of damper or mechanical shock absorber as before.
The crews in the outer two modules underwent symmetrical journeys. The crew of the central module went nowhere. Let us now consider the relationship between the "stationary" central module and just one of the "moving" modules as it is approaching the "stationary" one.
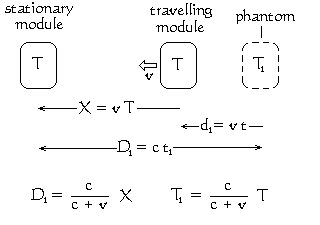
The diagram on the left shows the "travelling" module approaching the "stationary" module at velocity v. Below it are the formulae for the distance D1 of the phantom and the time T1 shown on its clock. In all the scenarios so far, I consider the velocity of the "travelling" module v to be constant. Consequently, the expression c / (c + v) is also constant. This means that the velocity of the phantom is always proportional to the velocity of the "moving" module.
These formulae for the return journey are the same as those for the outward journey. However, on the return journey, the velocity, v is, by convention, negative.
On the outbound journey, as the velocity of the module is increased linearly, the velocity of its phantom increases only logarithmically. Even though the velocity of the phantom increases with that of the module, the phantom lags more and more behind the reality of the "travelling" module. On the return journey, however, the velocity of the phantom increases exponentially with linear increase of the velocity of the module. So, on the return trip, the phantom is really travelling! Thus there is an enormous asymmetry between the velocity of the outbound phantom and the velocity of the phantom of the returning module.
The Triplets Paradox
Suppose the 3 middle modules of the 5-module spaceship each contains 1 of 3 triplets. One of the triplets is in the middle module which, throughout the whole of the 14-year experiment, goes nowhere. The two other triplets travel outwards in opposite directions for 7 years and then spend 7 years returning to their brother in the middle module. Are they all the same age when they return? Or has time for the travelling triplets dilated, leaving them younger than their "stationary" brother?
While they are travelling relative to each other at a significant proportion of the speed of light, the reality of each of the triplets is outside the event horizons of his two brothers. Each is, in effect, totally disconnected from his brothers. Each is therefore, in effect, in a different universe. The only aspects of his brothers, that lies within the event horizon of any one of the triplets, are their relativistic phantoms.
From the point of view of the "stationary" triplet, the phantom clocks of his two brothers appear to be running at a different speed from his clock. Their clocks appear to be running slower when receding and faster when approaching. From the point of view of either one of the "travelling" triplets, the clock within the phantom of his "stationary" brother will appear to be running less 'faster' or 'slower' than the clock within the phantom of his "travelling" brother.
The journeys of the two travelling triplets are identical, except that they journeyed in opposite directions. There is no evidence to suppose that the rate at which time passes be different in one direction than in another. Consequently, no matter how the clock within the phantom of one travelling triplet's module appeared to behave from the point of view of the other travelling triplet during the journey, time for each should be the same when they reunite. They must both have aged by the same amount, namely 14 years.
At the beginning of his journey, each of the two travelling triplets was accelerated to a large proportion of the speed of light. Their respective accelerations were in opposite directions. But there is no physical reason why the temporal effect of acceleration on a body must be different in different directions. Consequently, since they accelerated by the same amount, any resulting temporal effect, suffered by the two travelling triplets, must have been the same. Their accelerations should not therefore produce a lasting time dilation between them.
During their journeys, each travelling triplet observes his brother as a phantom for whom time passes slower while receding and faster when approaching. But once reunited, time for them both must be the same. Their illusion of time dilation or compression is therefore a function of how the rate of expansion or contraction of the distance between them affects the conveyance of information between them. It is nothing to do with the space each occupies or his position relative to any other position in space and time.
Consequently, any such illusion can exist only for so long as there is a changing amount of space between them. There is therefore no reason to suppose that their "stationary" brother, upon the reuniting of all three of them, should not be the same age as them. Indeed, if, upon being reunited, the triplets were not all the same age, then it must be possible for two different points in time to exist at one point in space-time, which is an absurdity.
Unlike their relationships to their brother on the stationary module, the journeys of the two travelling triplets form a perfect opposing symmetry. They each undergo the same accelerations equally and oppositely. Since their situations are totally symmetrical, how does space-time decide which of the two travelling triplets is to be younger and which is to be older than the other when they reunite? On what basis could there be any asymmetry between their ages after the journey? The idea of classical relativity that one of the travelling triplets should not have aged as much as the other when reunited isn't just a paradox: it's a logical nonsense.
Notwithstanding all the above, as covered in a previous article, the apparent dilation and compression in time, during the journeys, is only manifest for time in the plane perpendicular to the line of travel. Time along the axis of travel suffers only the illusion of cyclic asymmetry.
We need to explore the behaviour of a module and its phantoms more fully. However, to do so, we must be very careful about how we represent the most fundamental parameter involved here, namely time.
© 17 August 2006 Robert John Morton |
PREV |
NEXT


 This past phantom is how the "travelling" module was at some time t1 in the past. Here, t1 is the time that information takes to travel the distance D1 from the position of the phantom to the "stationary" module. Since the maximum velocity at which information can travel is that of light c, this distance must be given by D1 = c t1. The elapsed time T1 shown on the phantom's clock at elapsed time T on the clock of the "stationary" module must be given by T1 = T − t1.
This past phantom is how the "travelling" module was at some time t1 in the past. Here, t1 is the time that information takes to travel the distance D1 from the position of the phantom to the "stationary" module. Since the maximum velocity at which information can travel is that of light c, this distance must be given by D1 = c t1. The elapsed time T1 shown on the phantom's clock at elapsed time T on the clock of the "stationary" module must be given by T1 = T − t1.
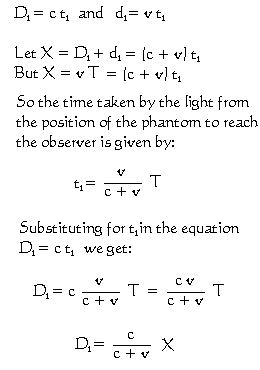 Let us now consider the distance D1 of the phantom from the observer in terms of the distance X of the reality from the observer. Intuition would suggest that, as the reality gets further and further away from the observer, its phantom will lag further and further behind. The adjacent algebra derives a formal expression for D1 in terms of X. This shows that if the velocity v of the "travelling" module is a constant, then D1 will be a constant fraction of X. If the "travelling" module were to travel at the velocity of light, its phantom would travel at half the velocity of light. If the "travelling" module were to travel at a million times the velocity of light, its phantom would travel at only 1,000,000÷1,000,001 times the velocity of light. That is 0·999999000000999999000000999999c. So however fast the reality travels relative to the observer, the observer sees it only as a phantom travelling at less than the velocity of light.
Let us now consider the distance D1 of the phantom from the observer in terms of the distance X of the reality from the observer. Intuition would suggest that, as the reality gets further and further away from the observer, its phantom will lag further and further behind. The adjacent algebra derives a formal expression for D1 in terms of X. This shows that if the velocity v of the "travelling" module is a constant, then D1 will be a constant fraction of X. If the "travelling" module were to travel at the velocity of light, its phantom would travel at half the velocity of light. If the "travelling" module were to travel at a million times the velocity of light, its phantom would travel at only 1,000,000÷1,000,001 times the velocity of light. That is 0·999999000000999999000000999999c. So however fast the reality travels relative to the observer, the observer sees it only as a phantom travelling at less than the velocity of light.
 The ratio between the distance X of the "travelling" module and the distance D of the phantom from the observer on the "stationary" module varies inversely with the velocity v of the "travelling" module. Their velocities should also be in this same ratio. The graph on the left uses this ratio to plot the velocity of the phantom against the velocity of the "travelling" module in units of c, the velocity of light. Ignore just for the moment the physical "legality" of the module travelling beyond the speed of light. We see that, however fast the module itself travels, its phantom — what is to the observer the effective physical reality of the module — can never attain the speed of light.
The ratio between the distance X of the "travelling" module and the distance D of the phantom from the observer on the "stationary" module varies inversely with the velocity v of the "travelling" module. Their velocities should also be in this same ratio. The graph on the left uses this ratio to plot the velocity of the phantom against the velocity of the "travelling" module in units of c, the velocity of light. Ignore just for the moment the physical "legality" of the module travelling beyond the speed of light. We see that, however fast the module itself travels, its phantom — what is to the observer the effective physical reality of the module — can never attain the speed of light.
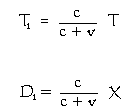 From the above, we have seen that — from the point of view of the observer — the time on-board the "travelling" module dilates by an amount given by the formula...
From the above, we have seen that — from the point of view of the observer — the time on-board the "travelling" module dilates by an amount given by the formula...
 In the diagram on the left, Dn is the distance of the near end of the phantom from the observer's eye on-board the "stationary" module. Correspondingly, Df is the distance of the far end of the phantom. Df is greater than Dn by an amount equal to the length of the phantom image of the "travelling" module. It therefore takes the light a little longer to reach the observer's eye from the far end of the "travelling" module than it does from its near end. This extra time is L/c, where L is the length of the phantom.
In the diagram on the left, Dn is the distance of the near end of the phantom from the observer's eye on-board the "stationary" module. Correspondingly, Df is the distance of the far end of the phantom. Df is greater than Dn by an amount equal to the length of the phantom image of the "travelling" module. It therefore takes the light a little longer to reach the observer's eye from the far end of the "travelling" module than it does from its near end. This extra time is L/c, where L is the length of the phantom.

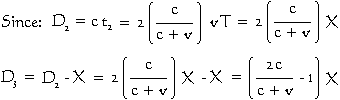

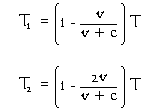 Furthermore, the rate at which time is observed to pass is different for each phantom. The "stationary" observer sees the elapsed time on the clock inside the first phantom as T1 whereas the "travelling" observer sees the elapsed time on the clock inside the second phantom as T2 as shown on the right. The observed "travelling" module is moving away from the "travelling" observer twice as fast as it is from the "stationary" module. Consequently, the clock in the second phantom appears to run at only half the speed of the clock in the first phantom.
Furthermore, the rate at which time is observed to pass is different for each phantom. The "stationary" observer sees the elapsed time on the clock inside the first phantom as T1 whereas the "travelling" observer sees the elapsed time on the clock inside the second phantom as T2 as shown on the right. The observed "travelling" module is moving away from the "travelling" observer twice as fast as it is from the "stationary" module. Consequently, the clock in the second phantom appears to run at only half the speed of the clock in the first phantom.