Revolution is the name of a kind of motion, which any object may have. It is the kind of motion in which the object moves, in a circle, around a centre. To be pedantic, its path may not be exactly circular. It could, in general, be an ellipse or even a rosette shaped path, which is made up of successive open ellipses. Notwithstanding, revolution is essentially an object travelling repeatedly around some point or centre. For example, the Earth revolves around the Sun in an annual cycle. The Moon revolves around the Earth in a monthly cycle.
Rotation, on the other hand, is when an object spins around an axis through the centre of the object itself. For example, the Earth rotates once a day. The Sun rotates ostensibly once every 26 days. However, any object is made up of smaller objects such as atoms. Thus, the atoms, of which the object is composed, are revolving around an axis through the centre of the object. Consequently, rotation is strictly a special case of revolution. It is merely collective revolution. Revolution is the fundament.
There are two ways in which an object can revolve. In other words, there are two modes of revolution. There is active revolution and there is passive revolution.
Passive revolution is where an object is revolving in a neutral state. This means that no real force is acting to sustain the object in its state of revolution. An example of passive revolution is the Earth revolving in orbit around the Sun.
Active revolution is where the exertion of a centripetal force is necessary in order to maintain the object in its state of revolution. A centripetal force is a real externally-applied force. It is not an inertial force. An example of active revolution is swinging a weight around your head on the end of a string. The string exerts a centripetal force upon the weight to keep it from flying off on a tangent.
Æthereal Flow
Before discussing the mechanisms of passive and active revolution, I wish to make a distinction in which a sink-hole is affected by æther flowing past it. Essentially, the universe comprises a flowing essence, which I have called æther. It flows continually — at the velocity of light — from the outer reaches of the universe into minuscule entities, which I have called sink-holes. In a non-flowing state, æther does not exist. It is a flow or flux. This æthereal flux is what gives human consciousness the perception of time.
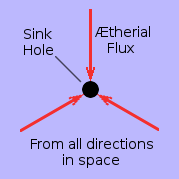 Considered in isolation, a sink-hole is a conceptual hole in space into which the universal æther continually flows from all directions equally in 3-dimensional space. A sink-hole is not dynamically affected by its own incoming flow of æther. This is because, from its own point of view, its own incoming flow is always symmetrical. It can only be perturbed by an asymmetry in the flow of æther in its vicinity. In other words, it can only be physically accelerated by a net flow of æther which is flowing through it, across it or past it but not into it.
Considered in isolation, a sink-hole is a conceptual hole in space into which the universal æther continually flows from all directions equally in 3-dimensional space. A sink-hole is not dynamically affected by its own incoming flow of æther. This is because, from its own point of view, its own incoming flow is always symmetrical. It can only be perturbed by an asymmetry in the flow of æther in its vicinity. In other words, it can only be physically accelerated by a net flow of æther which is flowing through it, across it or past it but not into it.
 However, if all the æther in the universe is flowing into sink holes, where does the æther, which flows through, across or past them, come from? The answer is, of course, the æther flowing into other sink holes. Across any point P in space, æther is flowing, in every direction, into what is ostensibly a homogeneous distribution of sink-holes S1, S2, S3 and so on, which populates the whole of space. Consequently, far from the immediate influence of any local sink-hole, the flow of the æther across any point P in space is spherically symmetrical both to and from any direction.
However, if all the æther in the universe is flowing into sink holes, where does the æther, which flows through, across or past them, come from? The answer is, of course, the æther flowing into other sink holes. Across any point P in space, æther is flowing, in every direction, into what is ostensibly a homogeneous distribution of sink-holes S1, S2, S3 and so on, which populates the whole of space. Consequently, far from the immediate influence of any local sink-hole, the flow of the æther across any point P in space is spherically symmetrical both to and from any direction.
This view of æthereal flow is what causes the inertial reaction to the forced acceleration of an object. In an orbital situation, it is what stops the planets or sink-holes falling towards each other along radial paths.
Thus, far from the immediate influence of any local sink-hole, the flow of æther into a sink hole and the flow of æther through, across or past a sink hole are both spherically symmetrical. Consequently, neither can have any perturbing effect on any sink hole. Notwithstanding, any asymmetry in the distribution of sink holes in a given locality causes a corresponding asymmetry in the æthereal flux passing through or across any given point P in that locality. Any sink hole, at that point, will consequently suffer an acceleration in the direction of net æthereal flux.
Revolution, rotation and orbits involve two separate mechanisms which generate, respectively, convergent and divergent versions of æthereal flux asymmetry.
Free Mutual Attraction
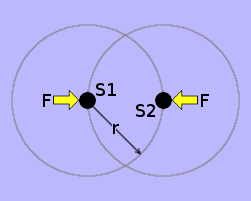
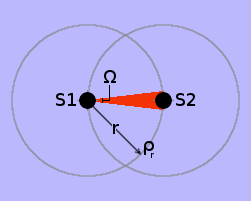 The mechanism of mutual attraction between two sink holes, in an otherwise empty universe, is illustrated on the right. However, only the mechanism whereby S1 attracts S2 is actually shown. Equally, S2 attracts S1, thus making the attraction mutual. The full explanation of this mechanism appears in my earlier essay: The Enigmatic Æther. Essentially, the spherically-symmetrical in-flow of æther into S1 passes S2, creating an asymmetrical flux across S2, which causes S2 to accelerate towards S1.
The mechanism of mutual attraction between two sink holes, in an otherwise empty universe, is illustrated on the right. However, only the mechanism whereby S1 attracts S2 is actually shown. Equally, S2 attracts S1, thus making the attraction mutual. The full explanation of this mechanism appears in my earlier essay: The Enigmatic Æther. Essentially, the spherically-symmetrical in-flow of æther into S1 passes S2, creating an asymmetrical flux across S2, which causes S2 to accelerate towards S1.
Likewise, of course, the spherically-symmetrical in-flow of æther into S2 passes S1, creating an asymmetrical flux across S1, which causes S1 to accelerate towards S2. Note that in both cases, the æthereal flux flowing spherically-symmetrically into a sink hole, from all directions in space, plays no part in its own acceleration towards the other sink hole.
Please note my use of the word "accelerate" in the previous two paragraphs. It is important to note that this is passive acceleration. Although the sink holes approach each other with ever-increasing velocity through space, this is not as a result of a directed external force: the sink holes are merely "going with the flow" of the æther.
Any macroscopic object, such as a planet, is, according to my hypothesis, a vast homogeneous agglomeration of sink holes. So the mutual "gravitational" attraction between two planets is a result of the action of exactly the same mechanism as described above.
Restrained Mutual Attraction
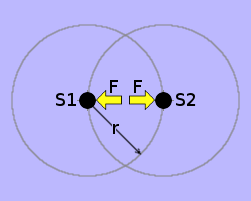 Suppose it's possible to hold sink holes S1 and S2 in place so that they can't move. To do this, it is necessary to apply a real directed force F, to each sink hole, in the direction away from its attractor. Let's imagine that the forces are applied by the Fingers of God. The sink holes experience real directed forces. But they are not accelerating through space. Each is in exactly the same situation as a person standing on the Earth experiencing the upward force of the ground on the bottoms of his feet.
Suppose it's possible to hold sink holes S1 and S2 in place so that they can't move. To do this, it is necessary to apply a real directed force F, to each sink hole, in the direction away from its attractor. Let's imagine that the forces are applied by the Fingers of God. The sink holes experience real directed forces. But they are not accelerating through space. Each is in exactly the same situation as a person standing on the Earth experiencing the upward force of the ground on the bottoms of his feet.
In the absence of any external force, the two sink-holes each "go with the flow" of the other's in-flowing æther passing by. This causes the sink-holes to accelerate towards each other until they collide. However, if an external force F is applied to keep them apart, it causes an asymmetry in the flow of the æther past each of them.
 Consider one of the sink-holes in isolation. The Finger of God exerts an external force F upon the sink-hole. This causes the sink hole to accelerate at a metres per second per second in the direction of the force. The sink hole is thus no longer "going with the flow" of its surrounding æther. This causes the flux density of the æther, flowing in the vicinity of the sink hole, to become spherically asymmetrical. This is depicted by the grey egg-shaped contour of constant flux density ρ in the diagram.
Consider one of the sink-holes in isolation. The Finger of God exerts an external force F upon the sink-hole. This causes the sink hole to accelerate at a metres per second per second in the direction of the force. The sink hole is thus no longer "going with the flow" of its surrounding æther. This causes the flux density of the æther, flowing in the vicinity of the sink hole, to become spherically asymmetrical. This is depicted by the grey egg-shaped contour of constant flux density ρ in the diagram.
One way of looking at this situation is to imagine that, when a force F impedes the sink hole's natural tendency to "go with the flow" of the æther, it causes an æthereal bow-wave to form on the opposite side of the sink hole to that on which the Finger of God applies the force. This æthereal bow-wave produces the inertial reaction I.
I will, for the time being, leave this force F, exerted upon each sink hole by the Fingers of God, as a conceptual place-holder to be replaced by something concrete later on. However, in order to be able to construct this concrete replacement for F, it is first necessary to investigate the mechanism of constrained revolution.
Constrained Revolution
My favourite example of constrained orbit is the wheel-shaped space station in the film "2001: A Space Odyssey". The station's accommodation is inside a hollow torus-shaped tube. This forms the rim of a big wheel, which rotates slowly. The rotation causes the station's inhabitants within the tube to experience their own weight, as they would on Earth, thus allowing them to walk, sit, eat, work and rest normally. In conventional terms, the force of this "artificial gravity" acts outwards from the centre of rotation in all directions. People walk on the inner wall of the torus with their feet furthest from the centre of the wheel and their heads towards its centre.
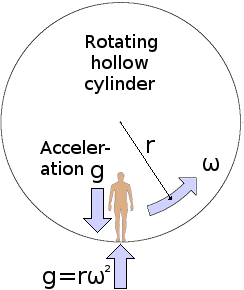 The principle of constrained revolution, is shown on the left in terms of a hollow rotating cylinder in free space. To create the sensation of Earth's gravity, it is necessary to make rω² = g, in which r is the radius of the cylinder, ω is the angular velocity with which the cylinder is rotating and g is the so-called acceleration of gravity at the Earth's surface, which is 9·80665 metres per second per second. A cylinder with a radius of 100 metres would therefore have to rotate at an angular velocity ω = √(g÷r) = √(9·80665÷100) = 0·313155712 radians per second to produce an "artificial gravity" of equal strength to that at the Earth's surface. This means that the cylinder would have to rotate once approximately every 20 seconds.
The principle of constrained revolution, is shown on the left in terms of a hollow rotating cylinder in free space. To create the sensation of Earth's gravity, it is necessary to make rω² = g, in which r is the radius of the cylinder, ω is the angular velocity with which the cylinder is rotating and g is the so-called acceleration of gravity at the Earth's surface, which is 9·80665 metres per second per second. A cylinder with a radius of 100 metres would therefore have to rotate at an angular velocity ω = √(g÷r) = √(9·80665÷100) = 0·313155712 radians per second to produce an "artificial gravity" of equal strength to that at the Earth's surface. This means that the cylinder would have to rotate once approximately every 20 seconds.
The so-called "gravitational acceleration", g, suffered by the body of a person standing on the wall of the rotating cylinder, is — according to the ideas I have been proposing throughout this series of essays — produced by the local radial flux-density gradient of the universal æther flowing radially outwards, at constant velocity c, through the person's body.
To prevent the person's body from "going with the flow" of the æther, the inner surface of the wall of the cylinder must exert a centripetal force F = mrω², where m is the so-called "mass" of the person's body.
Of course, this so-called "artificial" gravity is not artificial: it is just as much a natural phenomenon as is the gravity of a planet. Notwithstanding, it is a very different natural phenomenon. The gravitational flux converges spherically into a planet from all directions in 3-dimensional space. The gravitational flux generated by rotation, on the other hand, diverges cylindrically. It diverges from a line: not from a point. That line is the axis of rotation through the centre of the cylinder. I think that this is a fundamentally important distinction.
 A large rotating cylinder with people walking, sitting, eating, working and resting inside its torus-shaped rim is systemically complicated. I must abstract the essence of this phenomenon of "rotational gravity" and encapsulate it in a simpler form. For this purpose, I shall replace the rotating cylinder with a rotating dumbbell, as illustrated on the right, comprising two weights, joined together by a rigid weightless bar.
A large rotating cylinder with people walking, sitting, eating, working and resting inside its torus-shaped rim is systemically complicated. I must abstract the essence of this phenomenon of "rotational gravity" and encapsulate it in a simpler form. For this purpose, I shall replace the rotating cylinder with a rotating dumbbell, as illustrated on the right, comprising two weights, joined together by a rigid weightless bar.
The weights are sufficiently small and far apart for any "gravitational" attraction between them to be negligible compared with the centripetal force [pull] exerted upon them by the bar that joins them together.
Suppose that, while they are joined together by the rigid weightless rod, the two constrained weights are forcibly accelerated to an angular velocity ω. Once rotating at ω each weight suffers a real physical centripetal force, F = m† × r × ω², which is delivered through the rod and acts towards the centre of rotation.
† The constant m is known conventionally as the mass of the weight. However, as I have been proposing in this series of essays, m = k × n, where n is the number of æthereal sink-holes within the planet and k is a universal constant of proportionality.
Revolving Sink-Holes
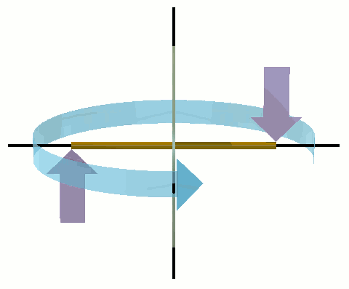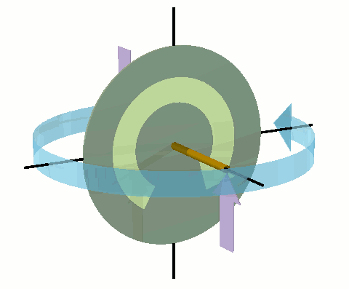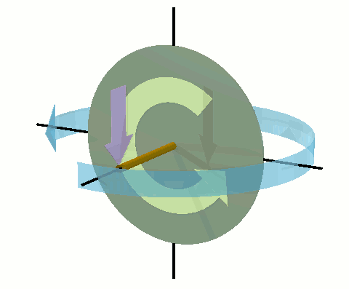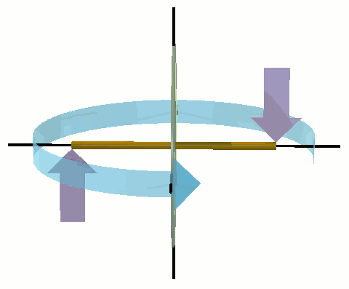
 The weights mentioned above are merely vast agglomerations of sink holes. I may therefore replace each weight by a single sink hole. In doing so, however, I must also replace the centripetal force, exerted by the weightless bar, with a pair of inward opposing forces F exerted by the Fingers of God. The two sink holes are thus now in constrained revolution around the common centre. In this case, each of the revolving weights comprises just one sink hole: i.e. n = 1.
The weights mentioned above are merely vast agglomerations of sink holes. I may therefore replace each weight by a single sink hole. In doing so, however, I must also replace the centripetal force, exerted by the weightless bar, with a pair of inward opposing forces F exerted by the Fingers of God. The two sink holes are thus now in constrained revolution around the common centre. In this case, each of the revolving weights comprises just one sink hole: i.e. n = 1.
The aspect of each sink-hole's revolutionary motion, which is the easiest for a human being to perceive, is that the sink-hole is proceeding around a circular path at a constant velocity. However, æther is a velocity fluid. It does not manifest itself, in any way, to an object that is not accelerating. Consequently, this aspect of the sink-hole's motion cannot cause it to react in any way with the æther.
Notwithstanding, in a purely conceptual sense, the sink-hole is accelerating. Yet it is not acelerating through space — at least, not in the way in which nature has equipped human beings to perceive acceleration through space. This is because the sink-hole is accelerating in a direction which is perpendicular to its orbital track. The direction in which the sink-hole is accelerating, as a result of its orbital motion, is radially inwards towards its orbital centre.
The centripetal force Fp which is necessary to accelerate each sink hole sufficiently to constrain it to revolve around the common centre of revolution is given by:
| Fp | = −½ × k × (n = 1) × r × ω²
|
| = −½krω²
|
The ½ is because r is twice the distance from a sink hole to the sink holes' common centre of revolution. The minus sign is because I have adopted the arbitrary convention that radially outward accelerations are positive and radially inward accelerations are negative.
How does the constraining of the two sink holes, by the forces F, to revolve about their common centre of revolution, affect the symmetry of the æthereal flux density in the vicinity of each one?
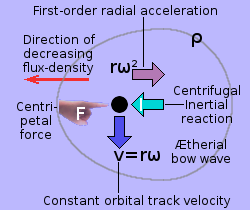 Whenever external forces F are applied to two sink-holes, to keep them revolving around each other, the otherwise spherically symmetrical æthereal flux passing by each sink-hole becomes asymmetrical. This creates an up-stream density bow wave as depicted by the egg-shaped grey contour in the diagram on the right. However, each force F and its inertial reaction I now act in the opposite sense from what they did in the case of mutual attraction. The direction of decreasing æthereal density is also reversed, as is that of the æthereal bow-wave.
Whenever external forces F are applied to two sink-holes, to keep them revolving around each other, the otherwise spherically symmetrical æthereal flux passing by each sink-hole becomes asymmetrical. This creates an up-stream density bow wave as depicted by the egg-shaped grey contour in the diagram on the right. However, each force F and its inertial reaction I now act in the opposite sense from what they did in the case of mutual attraction. The direction of decreasing æthereal density is also reversed, as is that of the æthereal bow-wave.
Note that, in the absence of any external forces F, the two "orbiting" sink-holes each "go with the flow". However, because they are not now accelerating in any way at all, each continues, at whatever relative velocity it has to its orbital partner, off at a straight tangent. The two sink-holes thus recede from each other forever.
 So far, I have ignored the real and present mutual attraction (discussed earlier) which the asymmetrical flow of each sink hole's æther across the other sink hole exerts upon that other sink hole. This is recapped in the illustration on the left. As I explained in the Enigmatic Æther, the magnitude of this force Fa = Γ ÷ r², where Γ is a natural universal constant. Compare this illustration with the previous one (above on right). The forces F, in each case, act in opposite directions.
So far, I have ignored the real and present mutual attraction (discussed earlier) which the asymmetrical flow of each sink hole's æther across the other sink hole exerts upon that other sink hole. This is recapped in the illustration on the left. As I explained in the Enigmatic Æther, the magnitude of this force Fa = Γ ÷ r², where Γ is a natural universal constant. Compare this illustration with the previous one (above on right). The forces F, in each case, act in opposite directions.
They act against each other. The net radial force acting within a system comprising a pair of revolving mutually attracting sink holes is therefore given by:
| f | = Fa + Fp
|
| = Γ ÷ r² − ½ × r × ω²
|
If f > 0 the sink holes fall towards each other in a decaying orbit.
If f = 0 the sink holes revolve about their common centre in a stable orbit.
If f < 0 the sink holes spiral away from each other in a expanding orbit.
For free orbit, the two place-holder forces F, represented by the Finger of God in the diagrams, are equal and opposite. Each is, in fact, the inertial reaction I (green arrow) in the opposing diagram. Thus, the two opposing inertial reactions are what holds the two sink-holes in mutual orbit around each other. This can only be properly represented by combining the two diagrams and summing the two contours of constant æthereal flux density to create a single envelope.
 The whole situation is clarified by the combined diagram on the right. The sink hole is shown in the dead centre of an ellipsoidal envelope of constant æthereal flux density ρ. This means that the centrifugal inertial reaction plus the so-called gravitational inertial reaction add up to zero. The æthereal flux, passing by the sink-hole, is thus rarer along the major axis of the ellipsoid — in both directions — than it is in any other direction relative to the sink hole.
The whole situation is clarified by the combined diagram on the right. The sink hole is shown in the dead centre of an ellipsoidal envelope of constant æthereal flux density ρ. This means that the centrifugal inertial reaction plus the so-called gravitational inertial reaction add up to zero. The æthereal flux, passing by the sink-hole, is thus rarer along the major axis of the ellipsoid — in both directions — than it is in any other direction relative to the sink hole.
Each successive contour of constant density thus has the form of a prolate ellipsoid, with the sink-hole at the centre. This ellipsoid is, however, conically distorted, with the point of the distorting cone being at the sink-hole's centre of revolution.
 Successive contours of constant æthereal flux density, which surround a sink hole alone in free space, are spherical, as shown on the left. On the other hand, the successive contours of constant æthereal flux density, which surround a sink hole in orbit, are not spherical.
Successive contours of constant æthereal flux density, which surround a sink hole alone in free space, are spherical, as shown on the left. On the other hand, the successive contours of constant æthereal flux density, which surround a sink hole in orbit, are not spherical.
 Successive contours of constant æthereal flux density, which surround a sink hole in free orbit with another, around their common centre of revolution, have the form of prolate ellipsoids. The major axes of these ellipsoids lie along the radial of revolution of the sink hole which they surround. Each sink hole lies at the centre of its concentric contours of constant flux density. The illustration on the right shows the situation for just one of the orbiting sink holes.
Successive contours of constant æthereal flux density, which surround a sink hole in free orbit with another, around their common centre of revolution, have the form of prolate ellipsoids. The major axes of these ellipsoids lie along the radial of revolution of the sink hole which they surround. Each sink hole lies at the centre of its concentric contours of constant flux density. The illustration on the right shows the situation for just one of the orbiting sink holes.
So there's a difference between a sink hole in free space and a sink hole in free orbit. The latter's (would-be spherical) contours of equal flux density are squashed around the radial of revolution to form prolate ellipsoids. Furthermore, these ellipsoids are conically distorted by containing cones, whose points (or apexes) lie at the centre of revolution. Consequently, being in free orbit is not quite the same as being completely alone in free space.
Planets in Free Orbit
 Consider two identical planets freely orbiting each other around a common centre, as shown in the animation on the left. According to the æthereal hypothesis, which I have been building throughout this series of essays, these two planets are in blissful equilibrium, But they are not in equilibrium between two equal opposing real directed forces.
Consider two identical planets freely orbiting each other around a common centre, as shown in the animation on the left. According to the æthereal hypothesis, which I have been building throughout this series of essays, these two planets are in blissful equilibrium, But they are not in equilibrium between two equal opposing real directed forces.
Instead, my hypothesis asserts that they are each in equilibrium between two opposing inertial reactions. And these two opposing inertial reactions result from two opposing æthereal flux density gradients.
Any macroscopic object, such as a planet, is, according to my hypothesis, a vast homogeneous agglomeration of sink holes. So the æthereal flux density contours surrounding a planet should be of the same form as those of a single sink hole. Consequently, for a solitary planet, far from the sight or influence of any other object, the successive contours of constant flux density are spherical. And for a planet in stable orbit, they have the form of prolate ellipsoids.
Convergent Acceleration
My term "convergent acceleration" refers to what most people at the present time think of as the spherically-convergent acceleration caused by gravitational attraction.
According to the ideas I have been putting forward in these essays, a solid object comprises a vast number of æthereal sink-holes. If the object is rotating, all these sink-holes are orbiting the object's axis of rotation at the same angular velocity, ω. However, each sink-hole is doing so at its own particular radial distance from the object's axis of rotation, rn where the subscript n identifies one particular sink-hole within the object. The nth sink-hole is thus accelerating through the æther at rnω² metres per second per second.
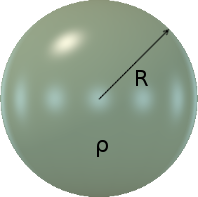 Consider an object like the green sphere on the right. It is perfectly at rest in free space. In other words, it is not accelerating. It is not in orbit around any other object. It is not rotating. It has a radius of R metres. According to my postulation, the substance of the sphere, at its most fundamental level, is composed of sink-holes. I shall take the liberty of assuming that these are homogeneously distributed, at least down to a small molecular level of granularity. I shall therefore consider the sphere to have a homogeneous density of ρ sink-holes per cubic metre.
Consider an object like the green sphere on the right. It is perfectly at rest in free space. In other words, it is not accelerating. It is not in orbit around any other object. It is not rotating. It has a radius of R metres. According to my postulation, the substance of the sphere, at its most fundamental level, is composed of sink-holes. I shall take the liberty of assuming that these are homogeneously distributed, at least down to a small molecular level of granularity. I shall therefore consider the sphere to have a homogeneous density of ρ sink-holes per cubic metre.
According to my hypothesis, a sink-hole, on the surface of the sphere will suffer an inertial acceleration a. This will be exactly countered by a real force, exerted by the rest of the sink-holes of the sphere, to stop the sink-hole in question from falling through "the ground" towards the centre of the sphere. Just like a person standing on the surface of the Earth suffers a downward acceleration of g. The magnitude of this inertial acceleration a on a single sink-hole located at the surface of the sphere is thus given by:
| a | = G × M ÷ R²
|
|---|
| But: | M | = k × n
|
|---|
| where: | n | is the number of sink-holes in the object
|
|---|
| and: | k | is a universal constant of proportionality
|
|---|
| Thus: | a | = G × k × n ÷ R² (1)
|
|---|
The number of sink-holes n, which makes up the substance of the sphere, is the volume V of the sphere times the sink-hole density ρ pertaining to the material of which the sphere is made.
| Thus: | n | = V × ρ
|
|---|
| but: | V | = (4/3) × π × R³
|
|---|
| so: | n | = (4/3) × π × R³ × ρ (2)
|
|---|
Substituting the expression for n given by equation (2) in equation (1):
| a | = G × k × (4/3) × π × R³ × ρ ÷ R²
|
| | = G × k × (4/3) × π × R × ρ
|
The quantities G, k and π are universal constants. I shall therefore
make the arbitrary choice to represent the product of these constants, together with the constant 4÷3, by the Arabic letter خ as follows:
| Let: | خ | = G × k × (4/3) × π
|
|---|
| Thus: | a | = خ × R × ρ (3)
|
|---|
Divergent Acceleration
My term "divergent acceleration" refers to what most people at the present time think of as the cylindrically-divergent acceleration caused by centrifugal repulsion away from a centre of revolution.
 Suppose now that the green sphere is rotating, as shown on the left, around an axis passing through its centre (black line), at an angular velocity of ω radians per second. I have postulated that all material objects are made up of æthereal sink-holes. Almost all the sink-holes, of which the green sphere is composed, will effectively be revolving around the sphere's axis of rotation at angular velocity ω. However, they will, for the most part, be revolving at different distances from the sphere's axis of rotation. Any sink-hole within the sphere, which is at a given orbital distance r from the axis of rotation, will suffer an inertial acceleration of rω², which acts radially outwards from the axis of rotation.
Suppose now that the green sphere is rotating, as shown on the left, around an axis passing through its centre (black line), at an angular velocity of ω radians per second. I have postulated that all material objects are made up of æthereal sink-holes. Almost all the sink-holes, of which the green sphere is composed, will effectively be revolving around the sphere's axis of rotation at angular velocity ω. However, they will, for the most part, be revolving at different distances from the sphere's axis of rotation. Any sink-hole within the sphere, which is at a given orbital distance r from the axis of rotation, will suffer an inertial acceleration of rω², which acts radially outwards from the axis of rotation.
 Consider the special case illustrated on the right of a sink-hole S, on the surface of the sphere, at the edge of the widest possible infinitely thin disc of radius R, whose plane is perpendicular to the sphere's axis of rotation. The sink-hole's spherically convergent inertial acceleration a = خRρ acts inwardly towards the centre of the sphere, while the sink-hole's cylindrically divergent inertial acceleration, Rω², caused by the sphere's rotation, acts outwardly away from the sphere's axis of rotation. Consequently, there must exist an angular velocity ωf at which Rωf² becomes equal and opposite to خRρ, leaving the sink-hole itself in the weightless state of free orbit.
Consider the special case illustrated on the right of a sink-hole S, on the surface of the sphere, at the edge of the widest possible infinitely thin disc of radius R, whose plane is perpendicular to the sphere's axis of rotation. The sink-hole's spherically convergent inertial acceleration a = خRρ acts inwardly towards the centre of the sphere, while the sink-hole's cylindrically divergent inertial acceleration, Rω², caused by the sphere's rotation, acts outwardly away from the sphere's axis of rotation. Consequently, there must exist an angular velocity ωf at which Rωf² becomes equal and opposite to خRρ, leaving the sink-hole itself in the weightless state of free orbit.
| Hence: | a = Rخρ | = −Rωf² | dividing both sides by R
|
|---|
| gives: | ωf² + خρ | = 0 | Zero net inertial acceleration (4)
|
|---|
 The resulting deformation in shape of the sink hole's otherwise spherical contours of constant æthereal flux density is shown on the left. They have become ellipsoidal. The sink hole is at the centre of the ellipsoids. This means that the centrifugal acceleration rωf² plus the so-called gravitational acceleration rخρ add up to zero. The æthereal flux passing the sink hole is thus denser along the major axis of the ellipsoids than it is in any other direction.
The resulting deformation in shape of the sink hole's otherwise spherical contours of constant æthereal flux density is shown on the left. They have become ellipsoidal. The sink hole is at the centre of the ellipsoids. This means that the centrifugal acceleration rωf² plus the so-called gravitational acceleration rخρ add up to zero. The æthereal flux passing the sink hole is thus denser along the major axis of the ellipsoids than it is in any other direction.
| Note: | if rωf² + rخρ > 0, the sink hole is off-set to the left within the ellipsoid.
|
| if rωf² + rخρ < 0, the sink hole is off-set to the right.
|
Of immediate interest here is that the angular velocity ωf, at which a sink-hole on the surface of the thin disc is in free orbit — i.e. weightless — is independent of the radius R of the sphere. The value of ωf is the same for any size of sphere made of the same material — or, more precisely, having the same sink-hole density, ρ.
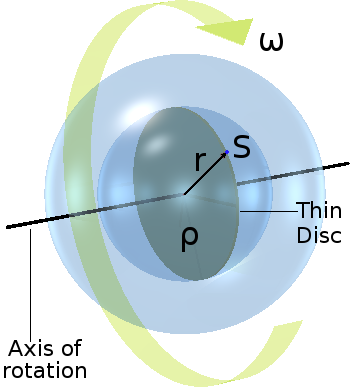 Now consider a sink-hole S, as shown on the right, within that same thin disc but not on its outer surface. This sink-hole is located at a radial distance r (less than R) from the sphere's axis of rotation. The spherically-symmetrical inward inertial acceleration a, acting upon this sink-hole, is خ × ρ × r. This is exactly the same as for a smaller sphere of total radius r. This is because, within the sub-sphere (stronger blue) of radius r, the influence of all the sink-holes that lie outside it — i.e. between the radius r and the radius R (lighter blue) — cancels to zero.
Now consider a sink-hole S, as shown on the right, within that same thin disc but not on its outer surface. This sink-hole is located at a radial distance r (less than R) from the sphere's axis of rotation. The spherically-symmetrical inward inertial acceleration a, acting upon this sink-hole, is خ × ρ × r. This is exactly the same as for a smaller sphere of total radius r. This is because, within the sub-sphere (stronger blue) of radius r, the influence of all the sink-holes that lie outside it — i.e. between the radius r and the radius R (lighter blue) — cancels to zero.
| Hence: | a = rخρ | = −rωf²
|
|---|
| giving: | ωf² + خρ | = 0 as before.
|
|---|
The upshot is that, when any sphere is rotating at angular velocity ωf, all the sink-holes within the largest infinitely thin disc passing through the sphere's centre and whose plane is perpendicular to the sphere's axis of rotation, become weightless. As I shall demonstrate later, they also lose inertia. Being without both weight and inertia implies that these sink-holes have become massless. This strongly suggests that the disc itself has become massless, or, at least, that mass itself isn't quite what we have always thought it to be.
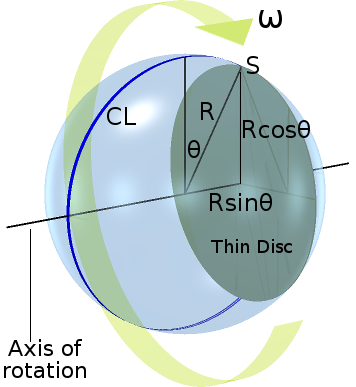 What about the sink-holes of the sphere that are outside this central thin disc? Consider a sink-hole S located on the sphere's surface at the edge of a smaller thin disc which is off-set along the axis of rotation at "latitude" θ from the sphere's "equator". This situation is shown on the left. CL is a circle of longitude, which passes twice through the axis of rotation — once at each "pole". The smaller thin disc (green) has a radius of Rcosθ and is off-set from the centre of the sphere along its axis of rotation by a distance of Rsinθ. As always, the sink-hole S suffers a spherically-symmetrical inward inertial acceleration of خρ, along the radial R, towards the centre of the sphere.
What about the sink-holes of the sphere that are outside this central thin disc? Consider a sink-hole S located on the sphere's surface at the edge of a smaller thin disc which is off-set along the axis of rotation at "latitude" θ from the sphere's "equator". This situation is shown on the left. CL is a circle of longitude, which passes twice through the axis of rotation — once at each "pole". The smaller thin disc (green) has a radius of Rcosθ and is off-set from the centre of the sphere along its axis of rotation by a distance of Rsinθ. As always, the sink-hole S suffers a spherically-symmetrical inward inertial acceleration of خρ, along the radial R, towards the centre of the sphere.
However, the sink-hole's cylindrically-divergent outward inertial acceleration a is now ω² × R × sin(θ). But it does not now act in exact opposition to خρ. It acts out of line. To produce a sufficient outward acceleration to counter the inward acceleration خρ, the critical angular velocity ωf must be increased such that:
| ωf² × R × cos(θ) | = خ × ρ × R
|
|---|
| ωf² | = خ × ρ ÷ cos(θ)
|
|---|
When θ is zero, cos(θ) is 1, so the formula becomes ωf² = خ × ρ, so the thin disc is not off-set at all. This situation is the special case discussed above. As θ increases, cos(θ) decreases, so ωf² must be greater. At the extreme, when the sink-hole S is at a pole — i.e. it is on the axis of rotation — cos(θ) becomes zero, making ωf² — and hence ω itself — infinite. Consequently, it can only ever be within part of a rotating sphere that "centrifugal" flux can overcome completely "gravitational" flux.
 Thus, any spinning object has both an inward æthereal flux asymmetry (bow wave) and an outward æthereal flux asymmetry (bow wave). These are depicted, as best as I am able to represent them, in the illustration on the right. The spinning object is spherical. This causes the profile of its æthereal flux asymmetry to have the form of an ellipsoidal disc. I have taken artistic license by showing the radius of the disc-shaped outward contour of constant flux density as being greater than that of the spherical inward contour of constant flux density. However, this is purely to help to make them separately visible.
Thus, any spinning object has both an inward æthereal flux asymmetry (bow wave) and an outward æthereal flux asymmetry (bow wave). These are depicted, as best as I am able to represent them, in the illustration on the right. The spinning object is spherical. This causes the profile of its æthereal flux asymmetry to have the form of an ellipsoidal disc. I have taken artistic license by showing the radius of the disc-shaped outward contour of constant flux density as being greater than that of the spherical inward contour of constant flux density. However, this is purely to help to make them separately visible.
It should be well noted that the outward flux asymmetry is independent of the inward flux asymmetry. If I were to increase my object's rate of spin, this would not affect its incoming flux asymmetry.
The Fly-Wheel Principle
 The special case, described above, of the central thin disc of a rotating sphere, is of particular interest. This is because, within this thin disc, it is possible for the two opposing æthereal density gradients to be equal and therefore cancel each other out. I would therefore like to explore this special case further. To do this, I shall remove the whole of the material of the sphere, except for this central thin spinning disc. The result is, in principle, the fly-wheel, as illustrated on the left, of radius R, rotating with angular velocity of ω radians per second around an axis which passes through its centre perpendicularly to the plane of the disc. The letter S signifies an arbitrary sink hole, located on the surface of the fly-wheel and which is itself part of the material of the fly-wheel.
The special case, described above, of the central thin disc of a rotating sphere, is of particular interest. This is because, within this thin disc, it is possible for the two opposing æthereal density gradients to be equal and therefore cancel each other out. I would therefore like to explore this special case further. To do this, I shall remove the whole of the material of the sphere, except for this central thin spinning disc. The result is, in principle, the fly-wheel, as illustrated on the left, of radius R, rotating with angular velocity of ω radians per second around an axis which passes through its centre perpendicularly to the plane of the disc. The letter S signifies an arbitrary sink hole, located on the surface of the fly-wheel and which is itself part of the material of the fly-wheel.
The cyan (light blue) arrow in the diagram represents the radially outward acceleration a suffered by the sink hole S as a result of the a real force exerted upon it by the material of the disc to oppose its natural tendency to "go with the flow" of the net æthereal flux flowing into all the other sink holes in the material of the disc.
| Acceleration, | a | = G × M ÷ R² [an experimental observation]
|
|---|
| But: | M | = k × n
|
|---|
| So: | a | = G × k × n ÷ R²
|
|---|
| But: | n | = V × ρ [volume × sink hole density]
|
|---|
| Therefore: | a | = G × k × V × ρ ÷ R²
|
|---|
So far, this is the same as previously derived for the rotating sphere. However, the volume of a thin disc is not (4/3)πR³ but πR² × l, where l is the thickness of the fly-wheel disc.
| So: | V | = π × R² × l
|
|---|
| Let: | q | = l ÷ R [the ratio between disc's thickness and radius]
|
|---|
| Therefore: | V | = π × R² × q × R
|
|---|
| | = π × q × R³
|
|---|
The volume V of the disc is thus still, like as with the sphere, a function of the cube of the radius. So, substituting this expression for V in the previous expression for the acceleration:
| Acceleration, | a | = G × k × π × q × R³ × ρ ÷ R²
|
|---|
| | = G × k × π × q × R × ρ
|
|---|
| Let: | ق | = G × k × π [a product of natural universal constants]
|
|---|
| a | = ق × ρ × q × R
|
|---|
| | = قρqR
|
|---|
The ratio q here stands for the disc where the ratio (4÷3) stood for the sphere. However, because the thickness of a disc is arbitrary, I decided not to include it in the universal constant ق.
Note that the magnitude of the inward acceleration is proportional to the number of sink holes within the agglomeration of sink holes that forms the disc and its direction is towards the centre of that agglomeration, namely, the centre of the disc. Thus, for any sink hole within the disc, the inward acceleration is the same as if all the substance of the disc were a sphere whose centre were coincident with the centre of the disc. The magnitude of the acceleration, in the case of the disc, is therefore given by the same expression قρqR as for a sphere of the same radius R.
The mauve arrow represents the radially outwards inertial acceleration −Rω² suffered by the sink hole S as a result of the sink hole's revolutionary motion around the disc's axis of rotation.
It is self-evident, therefore, that there must exist a particular angular velocity ωf at which the sink hole's centrifugal acceleration −Rωf² becomes equal and opposite to its inward "gravitational" acceleration قρqR, effectively placing the sink hole S in the weightless state of free orbit around the disc's axis of rotation. Thus, for any sink hole on the periphery of the disc:
| قρqR + Rωf² = 0 | is the condition for free orbit.
|
|---|
| R(قρq + ωf²) = 0 | Divide both sides of this equation by R
|
|---|
| thus: | قρq + ωf² = 0 | showing that the condition is independent of R.
|
|---|
This signifies that rotating the disc at the same angular velocity ωf will effectively put any sink hole within the material of the disc into the weightless state of free orbit around the disc's axis of rotation. This merely means that the inward and outward æthereal flux-density gradients are the same for the fly-wheel as a whole.
What is the value of ωf in radians per second for a practical fly-wheel disc? Consider a disc weighing 20kg of radius ½ a metre. The acceleration "due to gravity", as it is conventionally called, at the surface of the disc is given by:
| Acceleration, | a | = G × M ÷ R² ["gravitational"]
|
|---|
| | = 6·67408 × 10-11 × 20 ÷ (0·5)²
|
| (1) | | = 5·339264 × 10-9 metres per second per second
|
How fast will the fly-wheel disc have to rotate to cancel out the effect of its own "gravity"? The "centrifugal" acceleration, as it is conventionally called, at the surface of the disc is given by:
| Acceleration, | a | = −R × ω² ["centrifugal"]
|
|---|
| (2) | ω² | = |a ÷ R|
|
|---|
For a sink hole on the outer surface of the disc at its maximum radius of 0·5 metre to be in "free orbit", the two accelerations must have the same magnitude. To express this condition, I can substitute the "gravitational" value for a given by expression (1) in expression (2).
| ωf² | = 5·339264 × 10-9 ÷ 0·5
|
|---|
| | = 10·678528 × 10-9
|
|---|
| angular velocity, | ωf | = √(10·678528 × 10-9)
|
|---|
| | = 0·000103337 radians per second
|
|---|
| frequency, | ff | = 0·000016447 hertz
|
|---|
| | = 0·000986795 RPM
|
|---|
This means that the fly-wheel disc would have to rotate at the rate of once every 16 hours 53 minutes 23 seconds for its centrifugal effect to cancel out its gravitational attraction. Consequently, for all practical fly-wheel experiments, the value of قρqR is so extremely weak as to be well and truly negligible.
In contrast, within the scale of practical human experience, the term R × ω² has a very strong effect. In the space wheel mentioned earlier, to create the equivalent acceleration of the Earth's gravity, a 200 metre diameter space wheel need only rotate at a rate of once every 20 seconds. The rate of spin necessary for the 1 metre diameter fly-wheel disc, considered above, to accomplish a centrifugal acceleration equal to the acceleration of gravity on the Earth's surface is calculated below:

| acceleration, | g | = −R × ω² ["centrifugal"]
|
|---|
| ω² | = |−(g ÷ R)|
|
|---|
| ω | = √(g ÷ R)
|
|---|
| ω | = √(9·80665 ÷ 0·5)
|
|---|
| ω | = 4·428690551 radians/second
|
|---|
| rotation rate | f | = 4·428690551 ÷ (2 × π)
|
|---|
| | = 0·704847993 hertz
|
|---|
| | = 42·290879561 RPM
|
|---|
| period | p | = 1/f
|
|---|
| | = 1·418745616 seconds
|
|---|
The moving arrow, in the adjacent animation, shows the actual rate of spin (just over 42 RPM) necessary for the disc to generate a centrifugal acceleration equal to g, the acceleration due to the Earth's gravity at sea level. And as you can see, it is not very fast at all.
While rotating at this speed (just over 42 RPM), the disc's outward "centrifugal" acceleration is 1·83670446×109 (almost two billion) times its inward "gravitational" acceleration. Thus, on the practical human scale of fly-wheels, the "centrifugal" effect is overwhelmingly dominant compared with its opposing "gravitational" effect. The two opposing accelerations can therefore only interact on a humanly perceivable scale for very massive objects (like stars or planets) which are rotating very slowly.
[An interesting point of practical reference is that the popular 720 mm diameter bicycle wheel has to rotate at only 49·8 RPM to generate the acceleration of gravity g at the outer surface of its tyre. That is equivalent to riding the bike at just under 6·76 km/h — a slow jogging speed.]
Let us now return to consider the situation, within the disc itself, where the two oppposing accelerations are not necessarily equal. That is, where ω ≠ ωf, which is where R(خρ + ω²) ≠ 0. Clearly, it is not now possible to divide both sides of this inequality by R. Consequently any non-zero value of R(خρ + ω²), for any given sink hole within the fly-wheel, depends on the radius R of the fly-wheel. In general, for a fly-wheel of radius R, there are 3 possible situations for a sink hole located at distance r from the fly-wheel's axis of rotation, where 0 ≤ r ≤ R, which are:
1) r(خρ + ω²) > 0 Net real force acting radially outwards
2) r(خρ + ω²) = 0 No net real force acting on the sink hole
3) r(خρ + ω²) < 0 Net real force acting radially inwards
In case 1) above, the net force is equivalent to the force that acts upwards against the bottoms of your feet when you are standing on the Earth. Case 2) above is when the sink hole concerned is effectively in free orbit around the fly-wheel's axis of rotation. Case 3) above is a net force exerted by the material of the fly-wheel to hold the sink hole in place to stop it flying off at a tangent out of the fly-wheel.
The Gyroscopic Phenomenon
I remember clearly at school one day when we entered the physics laboratory for our lesson. There was our illustrious physics master Basher Bond. He was always enthusiastic about physics and earned the nickname "Basher" because he was naturally fit and muscular. That day, on a bench in the corner of the laboritory, was a little device humming gently to itself. It was a fully-gimballed gyro sustained by an integral electric motor. It had a rotating shaft protruding at one end. He told us to glance at it from time to time throughout our afternoon physics session.
We had learned, by practical demonstration, that a gyro resisted reorientation by external interference. We were therefore intrigued when it was observed that this gyro gradually shifted its axial orientation throughout the afternoon.
Basher said he would leave it running and we should look in on it the next morning and again in the afternoon, which would be 24 hours after our physics lesson. It transpired that the axis of the gyro went head over heels every 24 hours, yet did not return exactly to where it had been 24 hours earlier.
 The implication was that, unlike the pendulum that we had been studying previously, the gyro's frame of reference was not the Earth. Its orientation was not determined — or even influenced — by Earth's gravity. Instead, it seemed to strive to keep its axis aligned with an absolute direction in free space. So its frame of reference was not the Earth, the Sun or even the solar system. It was the Universe itself. It seems that a rapidly rotating mass has a mysterious directional coupling with space itself. And this coupling is quite strong. A gyro's insistence to keep its direction fixed with respect to the Universe, is evinced by two problems encountered when using the properties of the gyro to help with terrestrial navigation.
The implication was that, unlike the pendulum that we had been studying previously, the gyro's frame of reference was not the Earth. Its orientation was not determined — or even influenced — by Earth's gravity. Instead, it seemed to strive to keep its axis aligned with an absolute direction in free space. So its frame of reference was not the Earth, the Sun or even the solar system. It was the Universe itself. It seems that a rapidly rotating mass has a mysterious directional coupling with space itself. And this coupling is quite strong. A gyro's insistence to keep its direction fixed with respect to the Universe, is evinced by two problems encountered when using the properties of the gyro to help with terrestrial navigation.
For navigation, a gyro platform is used to provide a stable frame of reference, which will not be perturbed by the pitching rolling and yawing of the ship, aircraft or land vehicle in which it is installed. It requires a combination of 3 fully-gimballed gyros, each aligned in one of 3 mutually-perpendicular directions in free space. The platform is initialized by aligning the 3 gyro axes to the Earth's North-South, East-West and Up-Down directions.
The 1st problem encountered with a gyro platform is known as earth-rate drift. As the Earth rotates throughout the day, its North-South, East-West and Up-Down directions, at any given place on its surface, change with respect to the Universe as a whole. What would be a gradually-accumulating error in the platform orientation has to be continually corrected with reference to a chronometer.
The 2nd problem encountered with a gyro platform is known as transport wander. At any given time, because the Earth is spherical, the North-South, East-West and Up-Down directions are different, with respect to the Universe, at different places. Consequently, as the vehicle moves across the Earth's surface, the North-South, East-West and Up-Down directions change with respect to fixed directions in free space. And these changes are in addition to and independent of earth-rate drift. So this too must be continually corrected as the vehicle moves.
When I worked as a programmer of flight simulators, I had to simulate a proprietry gyrocompass unit down to component level, plus the terrestrial environment within which it operated onboard an aircraft. For this, I had to build spherical geometry functions to simulate both earth-rate drift and transport wander into my program.
Torque Versus Force-Couple
Before delving into gyroscopic effects, it is vital to make clear distinctions between:
- a force and its [in-line] reaction,
- a force-reaction couple, and
- a torque.
In earlier articles in this series, I have invoked the concept of a lone reactionless force. I took licence by imagining such a force as being exerted by "the finger of God". However, a force cannot exist alone. There is no such thing as a monoforce. "To every action [force], there is an equal and opposite reaction." That's probably the best known of all Newton's Laws. It is true. But it needs qualifying because it is only a special case like a circle is a special case for the orbit of a planet around a star. Newton's Law: "To every action [force], there is an equal and opposite [in-line] reaction." is illustrated on the far left in the following diagram.
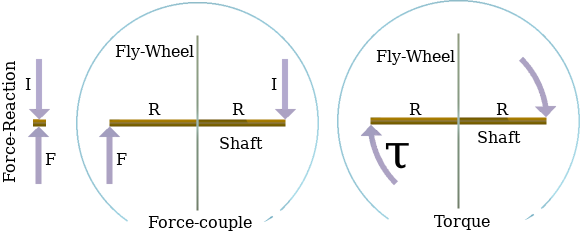
NOTE: The reaction is denoted by the letter I because, in the cases that I will be describing in the rest of this essay, the reaction will be an Inertial one, such as when the force F is what the ground exerts on the bottoms of your feet and the reaction I is the weight of your body; or, when the force F is the thrust produced by a rocket and the reaction I is the reluctance of the mass of the rocket to be accelerated. Within limited scope, these two situations have certain aspects of equivalence.
A force-couple is a force F and an ostensibly equal and opposite reaction I, which is not in line with F. The diagram shows an edge-on view of a fly-wheel on a shaft. F and I are each off-set by a distance R from what would be a potential centre of rotation.
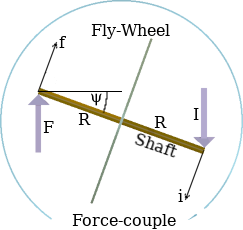 The diagram on the right shows what happens if the force-couple is allowed to act on the ends of the fly-wheel's shaft [assuming the fly-wheel isn't spinning] to rotate the fly-wheel by 20° around a line through its diameter.
The diagram on the right shows what happens if the force-couple is allowed to act on the ends of the fly-wheel's shaft [assuming the fly-wheel isn't spinning] to rotate the fly-wheel by 20° around a line through its diameter.
The force and its reaction both maintain their same respective directions in space. However, in order to remain acting at the ends of the shaft, each has to move laterally closer to the fly-wheel. Furthermore, the effective force couple now becomes f = F.cos(ψ) and i = I.cos(ψ) each acting at the same radius R.
A torque is different from a force-couple in that the forces are always tangential to the circle described when rotating the shaft about a diameter of the fly-wheel. However, although the torque τ can be represented by forces acting along the curve of the circle as shown on the right of the preceding main diagram above, this is merely a conceptual construct. A torque is a twisting action, so analysing it into any combination of circular force-couples acting at appropriate radii, whether symmetrically or asymmetrically, is essentially irrelevant.
Non-Rotating Fly-Wheel
The one-metre diameter fly-wheel disc rotating, even at only 42 RPM, as described and illustrated in the animation above, exhibits certain kinds of behaviour that are quite counter-intuitive to common human experience.
Consider the fly-wheel disc as being in free space far away from the influence of any other object. It is not spinning. To it, the distant star field of the universe is not rotating. The disc itself is not rotating. I have added to the disc a "massless" stub-shaft, which passes through the centre of the disc, perpendicular to its plane. The length of the stub-shaft is equal to the diameter of the disc. Thus the stub-shaft protrudes a distance R each side of the plane of the disc, where R is the radius of the disc, as shown in the following diagram.
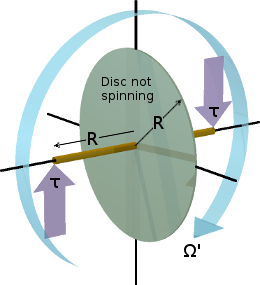 Let's apply a torque τ to the ends of the shaft as shown by the mauve coloured arrows. The torque τ is acting within a vertical plane which is perpendicular to the plane of the disc. The torque is attempting to rotate the disc around its horizontal diameter. This causes the disc to undergo an angular acceleration Ω' [dΩ/dt] around its horizontal diameter. This angular acceleration will continue as long as the torque τ continues to be applied. If and when τ is removed, the disc will continue rotating at the angular velocity it attained during the time that the torque was applied. To slow the rotation of the disc back down to zero again, the same torque τ must be applied in the opposite sense for the same amount of time.
Let's apply a torque τ to the ends of the shaft as shown by the mauve coloured arrows. The torque τ is acting within a vertical plane which is perpendicular to the plane of the disc. The torque is attempting to rotate the disc around its horizontal diameter. This causes the disc to undergo an angular acceleration Ω' [dΩ/dt] around its horizontal diameter. This angular acceleration will continue as long as the torque τ continues to be applied. If and when τ is removed, the disc will continue rotating at the angular velocity it attained during the time that the torque was applied. To slow the rotation of the disc back down to zero again, the same torque τ must be applied in the opposite sense for the same amount of time.
Note: Although the mauve arrows in the above diagram are straight and not curved, I am using them to represent the equivalent tangential forces at the ends of the fly-wheel's shaft. Notwithstanding, a torque is a twisting action, which must be considered as an integral phenomenon.
 But remember that a torque is more than simply a force-couple. It is what we may call a double force-moment: each half of this double force-moment comprises 1) an applied force and 2) a radial distance [at which the force acts] from the central axis-of-twist. The radial distance is ostensibly perpendicular to the direction of the force.
The two halves of a torque do not have to be symmetrical, although they usually are. One half of the torque can be a small force acting at a large radius, whereas the other can be a large force acting at a small radius. What must be symmetrical are the 2 half-moments of the torque; that is: force × radial distance must be the same for both halves.
But remember that a torque is more than simply a force-couple. It is what we may call a double force-moment: each half of this double force-moment comprises 1) an applied force and 2) a radial distance [at which the force acts] from the central axis-of-twist. The radial distance is ostensibly perpendicular to the direction of the force.
The two halves of a torque do not have to be symmetrical, although they usually are. One half of the torque can be a small force acting at a large radius, whereas the other can be a large force acting at a small radius. What must be symmetrical are the 2 half-moments of the torque; that is: force × radial distance must be the same for both halves.
The fly-wheel disc thus exhibits, what is conventionally termed, angular momentum, just like a small electric grindstone, which takes time for the motor to rev it up to its operating speed and time for friction to slow it down until it stops after the motor is switched off. Of course, when accelerated in this bizarre way, around its horizontal diameter, the disc doesn't exhibit the same amount of rotational impedance as it would if accelerated around its shaft axis. This is because, in this case, more of the disc is rotating at a smaller distance from its axis of rotation. There's nothing counter intuitive about this mode of rotation.
Rotating Fly-Wheel
 Now set the disc rotating around its shaft axis at angular velocity ω, as shown on the right. The modest 4·4 radians per second, of the previous animation, will suffice — just so long as this rate is maintained in the long term by some unspecified means. Now apply the torque τ as before. This time, the disc behaves differently. It does not rotate about the horizontal axis through its diameter as before. Instead, it rotates about its vertical diametric axis, as indicated by the circular blue arrow. Furthermore, it does not undergo an angular acceleration Ω'. Instead, it instantly acquires, and then continues to rotate at, a constant angular velocity Ω.
Now set the disc rotating around its shaft axis at angular velocity ω, as shown on the right. The modest 4·4 radians per second, of the previous animation, will suffice — just so long as this rate is maintained in the long term by some unspecified means. Now apply the torque τ as before. This time, the disc behaves differently. It does not rotate about the horizontal axis through its diameter as before. Instead, it rotates about its vertical diametric axis, as indicated by the circular blue arrow. Furthermore, it does not undergo an angular acceleration Ω'. Instead, it instantly acquires, and then continues to rotate at, a constant angular velocity Ω.
The angular velocity of Ω radians per second, taking place in the horizontal plane and indicated by the translucent blue arrow, is referred to as the fly-wheel disc's precession. The rate of precession (the value of Ω) is proportional to the value of the applied torque, τ. For example, if I double the torque, the rate of precession Ω doubles. The fly-wheel disc's rate of precession Ω is also inversely proportional to the angular velocity ω of the fly-wheel disc itself. For example, if I double the angular velocity ω of the fly-wheel disc, the rate of precession Ω halves.
The most significant observation for me, however, is that when the torque τ is removed, precession stops instantly. The fly-wheel disc does not keep on going as does a body in free space when a real directed force, which was accelerating it, is suddenly removed. Neither does the rate of precession Ω gradually slow down like the wheel of an electric grindstone does when it is switched off. Instead, precession stops instantly. The value of Ω instantly drops to zero.
To me, this implies that, in the horizontal plane at least, the fly-wheel disc has zero rotational inertia. Furthermore, since the torque τ cannot rotate the fly-wheel disc in the sense in which it (τ) is acting, the fly-wheel disc must have infinite rotational inertia around the torque axis. Of course, the fly-wheel disc still has rotational inertia around its axis of spin (its shaft axis). It would still require a considerable braking torque to kill the fly-wheel's spin.
 I find it very helpful to stare at the animation on the left while pondering on the above observations and their implications. Please click the animation for a larger view. One implication of the fly-wheel's apparent absence of rotational inertia around the vertical axis is as follows. Either, the disc has no angular inertia anyway within the horizontal plane of rotation, or, the disc's dynamic relationship with the universe does not change with the application or removal of the torque τ. In other words, the application of the torque τ does not accelerate the fly-wheel disc in any way.
I find it very helpful to stare at the animation on the left while pondering on the above observations and their implications. Please click the animation for a larger view. One implication of the fly-wheel's apparent absence of rotational inertia around the vertical axis is as follows. Either, the disc has no angular inertia anyway within the horizontal plane of rotation, or, the disc's dynamic relationship with the universe does not change with the application or removal of the torque τ. In other words, the application of the torque τ does not accelerate the fly-wheel disc in any way.
The second option, according to my hypothesis, implies that the torque τ does not cause the fly-wheel to move relative to the æther. Whether the torque is being applied or not — whether the fly-wheel be precessing or not — does not change the fly-wheel's dynamic relationship with the rest of the universe. It is — and remains — in the same state of rest with respect to the universe.
The angular velocity ω of the fly-wheel disc and the angular velocity Ω of precession are both rotational. Natural human intuition consequently led me (and others) to carelessly conclude that therefore the motive that produces the precession must also be rotational. That is, it must be a torque (or double force-moment) τ and not merely a simple linear force F. But is this true to rational observation?
Torque or Force?
To answer this question, I must bring the precessing fly-wheel disc down to Earth, where it is subject to the Earth's gravity.
 Spin the fly-wheel up to an angular velocity ω. Fix one free end of its shaft to a small cone-headed support stand via a universal ball or pin joint. The fly-wheel's rate of spin ω is maintained by unspecified means. The fly-wheel is observed to precess around the support stand at angular velocity Ω, as shown in the animation on the right.
Spin the fly-wheel up to an angular velocity ω. Fix one free end of its shaft to a small cone-headed support stand via a universal ball or pin joint. The fly-wheel's rate of spin ω is maintained by unspecified means. The fly-wheel is observed to precess around the support stand at angular velocity Ω, as shown in the animation on the right.
The fly-wheel appears to be suspended in thin air. Natural intuition would expect it to fall down. The end of the fly-wheel's half-shaft is simply resting on the point of the stand. It is not rigidly fixed to the stand. So it appears that the weight of the fly-wheel disc is being supported by some form of invisible cantilever fixed to the cone-headed stand. However, it is not even that simple because the measured upward force, exerted by the cone-headed stand, is only a small fraction of the fly-wheel's weight. In practical terms, it is probably no more than the weight of the shaft plus any non-rotating framework necessary for a practical apparatus. It appears that the fly-wheel disc has "lost" its natural weight — the weight it has when simply resting on the ground.
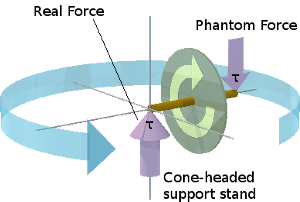 Conventional physics asserts that the fly-wheel is still being subjected to a torque τ. One half of τ's force-couple is thought to be the upward force, which the cone-headed support exerts upon the anchored end of the shaft. The other half-couple is imagined as an equal and opposite downward force exerted at the other end of the shaft, but which is, in really, thought to be double this force exerted downwards at the centre of the shaft by the weight of the fly-wheel.
Conventional physics asserts that the fly-wheel is still being subjected to a torque τ. One half of τ's force-couple is thought to be the upward force, which the cone-headed support exerts upon the anchored end of the shaft. The other half-couple is imagined as an equal and opposite downward force exerted at the other end of the shaft, but which is, in really, thought to be double this force exerted downwards at the centre of the shaft by the weight of the fly-wheel.
Notwithstanding, the conventional theory is problematic. Nothing is exerting a real directed downward force upon the fly-wheel. A real directed downward force would have to be applied by something material at a specific point on the outer surface of the fly-wheel, which clearly isn't the case. Let's take this apparatus into free space, far away from the sight or influence of any other object. Here, the support stand is a rocket, which is applying a thrust equal to the force F exerted by the support stand on Earth. Observation suggests that the fly-wheel will precess in exactly the same way. The only force in the system is the linear real directed force exerted by the rocket. No torque is involved.
Although there is no real torque-partner to the force of the rocket's thrust, there is, nonetheless, an inertial reaction to it. Normally, the inertial reaction to a real linear directed force, accelerating an object through space, is directly in line with, and in the opposite sense to, that force. I see the spinning precessing fly-wheel disc as a special case of a simple real directed force accelerating an object through space.
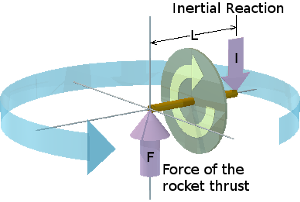 The thrust of the rocket exerts a force F, at the free end of the fly-wheel's shaft, perpendicular to the fly-wheel's axis of rotation, as shown on the right. This causes the fly-wheel to precess around the force's line of action. An equal and opposite inertial reaction I to the force F must exist. It does. However, the rotating precessing fly-wheel appears to have off-set this inertial reaction laterally from the line of action of the force.
The thrust of the rocket exerts a force F, at the free end of the fly-wheel's shaft, perpendicular to the fly-wheel's axis of rotation, as shown on the right. This causes the fly-wheel to precess around the force's line of action. An equal and opposite inertial reaction I to the force F must exist. It does. However, the rotating precessing fly-wheel appears to have off-set this inertial reaction laterally from the line of action of the force.
The torque formed by F and I are unable to rotate the fly-wheel about its diametric axis that is perpendicular to the line in which F acts. Consequently, the precessing fly-wheel acts as if it were a single solid object whose centre of mass is located at the point where the force from the rocket is being applied. The fly-wheel disc is thus being accelerated by the force F through space in line with the force. Furthermore, while the fly-wheel is freely spinning and precessing, the effective "mass" of what is being linearly accelerated through space is only a vanishingly small fraction of the static "mass" of the fly-wheel. Consequently, as far as I can see, the acceleration produced by the rocket must be very much greater than if it were accelerating the dead-weight of the fly-wheel when the fly-wheel wasn't spinning.
As can be seen from the diagram, the lateral off-set L of this equal and opposite inertial reaction I is the full length of the shaft. That is, it acts in a line that is as far again beyond the fly-wheel as the fly-wheel is from the point at which the rocket is applying the force F.
However, the double force-moment in this case could be asymmetrical. Thus I could be the inertial reaction to the full static-weight mass of the fly-wheel acting at a very small radius; that is: acting on the far half-shaft a mere smidgen the other side of the fly-wheel: not as shown in the above diagram. In fact, the far half of the "weightless" shaft doesn't even have to be there. If we chop it off, nothing will change. This implies that the action and its equal and opposite reaction [of Newton's Law] is merely a special case of a double force-moment where the force and its reaction are acting across a zero radius. Thus it is double force-moment [not force] that is the universal fundament.
This makes the situation in the above illustration comfortably intuitive. There is no imbalance, even though the torque acting on the fly-wheel appears at first sight to be asymmetric. This is because what is in equilibrium is not the force F and its inertial reaction I but the force-moment F × R and the other force-moment I × r, where R is the length of the half-shaft [also the radius of the fly-wheel] and r is the distance between the inertial reaction I and the point on the shaft where it acts, which, in reality, is just slightly the other side of the fly-wheel.
Back Down to Earth
Let us now go back to the Earth-bound situation, with the fly-wheel precessing around the support stand. Another counter-intuitive observation is that, if you try to stop the fly-wheel in its orbit of precession, practically no force is required. It just stops instantly and drops down to the ground. This is true, even if the fly-wheel itself be quite "massive". The implication is that, while precessing, the fly-wheel has lost inertia.
This deduction is substantiated by another observation. As the fly-wheel precesses around its orbit, there is practically no centripetal stretching force in the shaft. This implies that the motion of the fly-wheel around its orbit of precession produces little or no centrifugal "force".
Thus, it would seem that the fly-wheel has lost its inertia — at least, both radially and tangentially to its orbit of precession. In other words, the fly-wheel has lost both its mass and its inertia within the plane of precession: namely, the plane perpendicular to the force F.
I observed earlier that the spinning precessing fly-wheel had apparently lost its weight. It has also apparently lost its inertia along two mutually perpendicular axes which are both perpendicular to its would-be weight. Since, by convention, inertia and weight are both manifestations of the action of force upon mass, I think it is safe to conclude that the fly-wheel must have lost (at least most of) its mass.
All this is conceptually problematic. Notwithstanding, according to the theory I have been expounding in this series of essays, the fly-wheel did not have any mass in the first place, so it had none to lose. This is because what is conventionally perceived as mass is not a property of matter. It is a property of the relationship between an object and the density-gradient field of the space-time (or æther) within the vicinity of the object.
I previously defined what is conventionally perceived as an object's mass m in terms of the number of sink holes n in the object times a universal constant which I called k. Notwithstanding, the spinning precessing fly-wheel, as described above, reveals that, although k may be universal, it is only constant for objects that are neither spinning nor precessing. If an object, such as the fly-wheel disc described above, is spinning and precessing, k varies with the fly-wheel's rate of spin ω, its rate of precession Ω, the radius r of the fly-wheel and the radius R of its orbit of precession.
| Thus: | k | = kmax × function_of(ω, Ω, r, R) [generally k << kmax†]
|
|---|
| Since: | m | = n × k
|
|---|
| | m | = n × kmax × f(ω, Ω, r, R)
|
|---|
| Since: | F | = m × a [one of Newton's observations]
|
|---|
| then: | a | = F ÷ m [where m is the apparent mass of the fly-wheel]
|
|---|
| | = F ÷ {n × kmax × f(ω, Ω, r, R)}
|
|---|
† kmax is the value of k for a non-spinning non-precessing object.
This implies that, if the spinning fly-wheel were a large wheel-type space station, a small rocket mounted at the end of an axial tube, whose length was about equal to the space station's radius, could accelerate the space station as if it were a feather.
But this is all still counter-intuitive. It does not make sense in terms of general human experience of motion. So what exactly is going on here? What supports the fly-wheel vertically? Why doesn't it just fall like a dead weight would? Is it possible to interpret this gyroscopic phenomenon in terms of intuitive concepts? I'll try.
Asymmetrical Angular Velocity
 There is a significant asymmetry between the angular velocities of precession of the upper and lower halves of the fly-wheel.
Consider a pair of diametrically opposite sink holes on the outer rim of the fly-wheel disc. Spend some time contemplating the motions of the two sink holes [small red and green spheres] in the adjacent animation. Compare their motions as the fly-wheel spins and precesses.
There is a significant asymmetry between the angular velocities of precession of the upper and lower halves of the fly-wheel.
Consider a pair of diametrically opposite sink holes on the outer rim of the fly-wheel disc. Spend some time contemplating the motions of the two sink holes [small red and green spheres] in the adjacent animation. Compare their motions as the fly-wheel spins and precesses.
In the above animation, the angular velocity of the fly-wheel's rotation ω is exactly the same as its angular velocity of precession Ω. When the fly-wheel's axis of rotation is in line with the observer, it can be clearly seen that the upper sink hole's angular velocity of precession is zero, while the lower sink hole's angular velocity of precession is very high. In fact, it is twice Ω. This occurs when the fly-wheel is closest to the observer (red sink hole at the top) and also when the fly-wheel is furthest from the observer (green sink hole at the top). In both cases where the fly-wheel is side-on to the observer, the two sink holes are at the same level. Consequently, they are both, at these points, precessing around the orbit at the same angular velocity Ω. At all intermediate positions around the orbit of precession, the lower sink hole is always precessing faster, by some amount between zero and 2Ω.
The greatest difference between the angular velocities of precession of the upper and lower sink holes occurs at only two diametrically opposite points in the fly-wheel's orbit of precession. And it is the difference between the angular velocities, of the upper and lower sink holes, that is significant to the gyroscopic effect. Consequently, the gyroscopic effect only occurs in full at these points. At the points in the orbit where the fly-wheel is side-on to the observer, there is no difference in the orbital speeds of the two sink holes and therefore no gyroscopic effect at all. Notwithstanding, since there is an astronomical number of sink holes spaced around the circumference of the fly-wheel, there are always sink holes at the very top and the very bottom of the fly-wheel. Consequently, the gyroscopic effect is apparent and smooth all the way around the fly-wheel's orbit of precession.
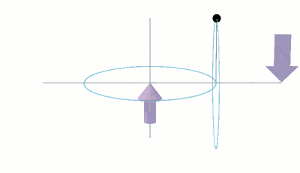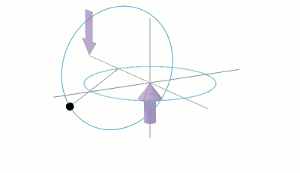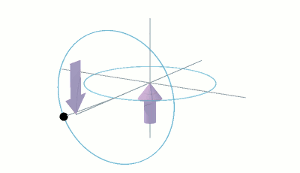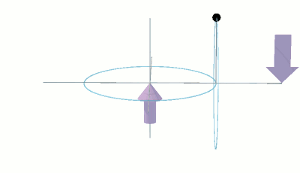 Now consider the motion of just one sink hole in the rim of the fly-wheel, as illustrated in the animation on the right. The sink hole moves a considerable distance, around the orbit of precession, while it is in the lower half of its journey around the rim of the fly-wheel. However, while in the upper half of its journey round the rim of the fly-wheel, the sink hole makes very little progress around the orbit of precession.
Now consider the motion of just one sink hole in the rim of the fly-wheel, as illustrated in the animation on the right. The sink hole moves a considerable distance, around the orbit of precession, while it is in the lower half of its journey around the rim of the fly-wheel. However, while in the upper half of its journey round the rim of the fly-wheel, the sink hole makes very little progress around the orbit of precession.
In fact, in the animation, where ω=5×Ω, it makes a little progress in the backwards direction. Thus, we could use a common colloquial expression here to describe the progress of the sink hole. We can say that, during its every revolution around the rim of the fly-wheel, it's taking "3 steps forward and two steps backward" around the orbit of precession. This means that the sink hole's velocity, around the orbit of precession, is much greater when it is below the fly-wheel's shaft than when it is above the fly-wheel's shaft.
The total angular velocity Ωs of the sink hole around the orbit of precession thus varies cyclically with every complete turn of the fly-wheel. The cyclic motion of the fly-wheel's spin is thus modulating the cyclic motion of its precession around the support stand. The nature of this modulation is as follows.
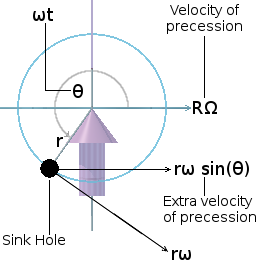 In the adjacent diagram, the viewer is looking along the fly-wheel's axis of rotation, from beyond the fly-wheel's orbit of precession, towards the support stand at the centre of the orbit. The fly-wheel is rotating anti-clockwise at an angular velocity of ω radians per second. The fly-wheel's direction of precession around its orbit is from left to right at a tangential velocity of RΩ metres per second, where R is the radius of the orbit in metres. The sink hole's tangential velocity around the fly-wheel is rω metres per second, where r is the radius of the fly-wheel in metres. The component of the sink hole's tangential velocity rω in the direction of orbital precession is rω.sin(θ).
In the adjacent diagram, the viewer is looking along the fly-wheel's axis of rotation, from beyond the fly-wheel's orbit of precession, towards the support stand at the centre of the orbit. The fly-wheel is rotating anti-clockwise at an angular velocity of ω radians per second. The fly-wheel's direction of precession around its orbit is from left to right at a tangential velocity of RΩ metres per second, where R is the radius of the orbit in metres. The sink hole's tangential velocity around the fly-wheel is rω metres per second, where r is the radius of the fly-wheel in metres. The component of the sink hole's tangential velocity rω in the direction of orbital precession is rω.sin(θ).
According to mathematical convention, the angle θ is measured from the positive horizontal direction (left to right). When 0 ≤ θ ≤ π, the sink hole is above the fly-wheel's axis of rotation. Over this range, sin(θ) is positive. When π ≤ θ ≤ 2π, the sink hole is below the fly-wheel's axis of rotation. Over this range, sin(θ) is negative.
| Thus the total tangential velocity: | R × Ωs | = R × Ω − r × ω × sin(θ)
|
|---|
| Divide the equation by R, giving:
|
|---|
| Total orbital angular velocity: | Ωs | = Ω − (r ÷ R) × ω × sin(θ)
|
|---|
The minus sign is because the arithmetic value of r × ω × sin(θ) is negative when the velocities are in the same direction. This is entirely due to the convention according to which the angle θ is measured. Thus, for any sink hole on the rim of the fly-wheel, Ωs is greater when the sink hole is below the fly-wheel's axis of rotation and less when the sink hole is above the fly-wheel's axis of rotation.
In order for the sink hole to be constrained to follow the orbit of precession, a real directed force Fs towards the centre of the orbit must be continually applied to it. This real directed force is a stretching force along the fly-wheel's shaft. This force Fs is transmitted to the sink hole on the rim of the fly-wheel by the radial strip of material at the end of which the sink hole lies.
 The sink hole is law-bound to exert an equal and opposite inertial reaction Is to the force Fs. As illustrated on the right, Is is much larger for a sink hole below the fly-wheel's axis of rotation than it is for a sink hole above it. The difference in Is for a sink hole below the fly-wheel's axis of rotation, and for a sink hole above it, forms an anti-clockwise torque around the fly-wheel's horizontal diameter, which the fly-wheel's shaft translates into a torque τs around the support point. Now let us consider the cumulative effect of all the sink holes that make up the material of the fly-wheel.
The sink hole is law-bound to exert an equal and opposite inertial reaction Is to the force Fs. As illustrated on the right, Is is much larger for a sink hole below the fly-wheel's axis of rotation than it is for a sink hole above it. The difference in Is for a sink hole below the fly-wheel's axis of rotation, and for a sink hole above it, forms an anti-clockwise torque around the fly-wheel's horizontal diameter, which the fly-wheel's shaft translates into a torque τs around the support point. Now let us consider the cumulative effect of all the sink holes that make up the material of the fly-wheel.
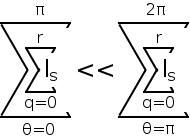 The inner sigma symbols, in the illustration on the left, are both the same. They sum the effects of all sink holes, within the material of the fly-wheel, which lie along an infinitely thin radial. That is, between q=0 and q=r, where q is a variable radius within the circle of the fly-wheel. The outer sigmas sum Is for all sink holes in the top half of the fly-wheel and all sink holes in the bottom half of the fly-wheel respectively.
The inner sigma symbols, in the illustration on the left, are both the same. They sum the effects of all sink holes, within the material of the fly-wheel, which lie along an infinitely thin radial. That is, between q=0 and q=r, where q is a variable radius within the circle of the fly-wheel. The outer sigmas sum Is for all sink holes in the top half of the fly-wheel and all sink holes in the bottom half of the fly-wheel respectively.
The illustration is saying that, at any given time, the cumulative centrifugal inertial reaction of all the sink holes in the top half of the fly-wheel Itop is much less than the cumulative centrifugal inertial reaction of all the sink holes in the bottom half of the fly-wheel Ibot. That is, Itop << Ibot. This explains where the inertial torque comes from which enables the fly-wheel to maintain its shaft horizontal while it is rotating and precessing.
Although the above explains where the torque necessary to support the fly-wheel comes from, it gives no clue as to why this rotating precessing state of the fly-wheel should be stable. There is no doubt that this dynamic state is stable. After all, if I momentarily pulse the fly-wheel upwards or downwards, it nutates. It bounces back and then continues to bounce up and down, with ever-diminishing amplitude, until its original state of smooth horizontal precession is re-established. This behaviour suggests to me that the whole dynamic system of the rotating precessing fly-wheel must contain some form of self-stabilizing negative feed-back.
Before we consider the full ramifications of nutation, it will be useful to examine another aspect of the precessing fly-wheel phenomenon.
Tilted Precession
 Suppose a fly-wheel is precessing in the horizontal plane as shown on the right. I apply a constant force to the precessing end of its shaft. An equal reactive horizontal force is resisted by the pivot. Thus, what is effectively being applied to the ends of the fly-wheel's shaft is a torque in the sense shown by the blue arrow.
Suppose a fly-wheel is precessing in the horizontal plane as shown on the right. I apply a constant force to the precessing end of its shaft. An equal reactive horizontal force is resisted by the pivot. Thus, what is effectively being applied to the ends of the fly-wheel's shaft is a torque in the sense shown by the blue arrow.
What does this applied torque cause to happen? It causes the shaft of the fly-wheel to tilt upwards, in a rotating vertical plane, with an angular velocity that is proportional to the torque. Note that applying the torque [which is the rotation equivalent of a force] does not cause the fly-wheel to undergo an upward angular acceleration, as one might expect. As soon as the torque is relaxed, the fly-wheel tilts upwards no further.
A torque has moved through an angle. Consequently, energy has been expended. But the same energy needs to be expended again to bring the fly-wheel back to horizontal precession. It is thus the act of changing the tilt of the fly-wheel that absorbs the energy, not the new tilted state itself. The act of tilting must therefore be a transducer that conveys the energy somewhere else. But this is a digression. Notwithstanding how it is brought about, I will now simply consider this tilted state of precession in it own right.
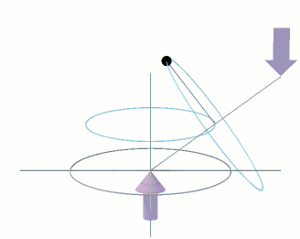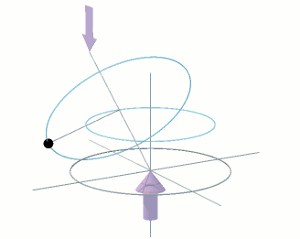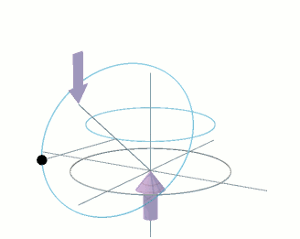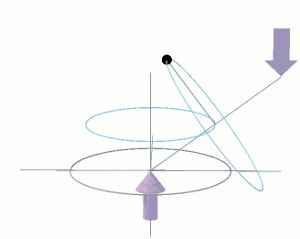 A spinning fly-wheel can adopt a mode of precession in which its shaft is tilted upwards from the horizontal as shown on the left. Its orbit of precession, which is smaller than before, can be thought of as a circle of latitude ψ on an imaginary sphere whose equator (the grey circle) was the fly-wheel's orbit of precession when its shaft was horizontal. The plane of the orbit of the sink hole around the rim of the fly-wheel is now no longer parallel to the direction of the force exerted by the support stand.
A spinning fly-wheel can adopt a mode of precession in which its shaft is tilted upwards from the horizontal as shown on the left. Its orbit of precession, which is smaller than before, can be thought of as a circle of latitude ψ on an imaginary sphere whose equator (the grey circle) was the fly-wheel's orbit of precession when its shaft was horizontal. The plane of the orbit of the sink hole around the rim of the fly-wheel is now no longer parallel to the direction of the force exerted by the support stand.
As can be seen from the animation, the sink hole's radius of precession is now much greater during its lower half-cycle than during its upper half-cycle, thus increasing the ratio between Ibot and Itop. This seems to exactly compensate for the fact that the orbital radius is now only R.cos(ψ), instead of R as it was when the fly-wheel's shaft was horizontal.
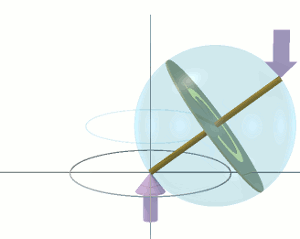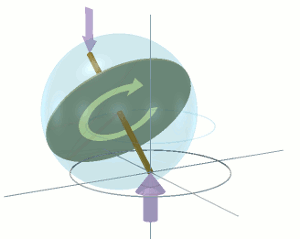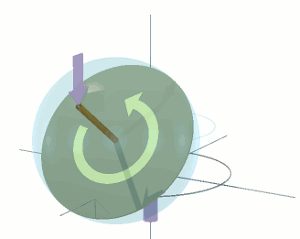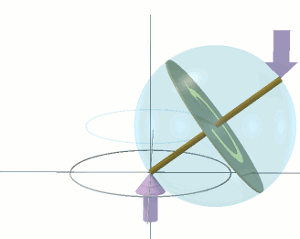 Now let us revert to considering the whole fly-wheel disc: not just a single sink hole on its outer rim. How can I cause a spinning fly-wheel to adopt this tilted mode of precession? Starting with the fly-wheel disc precessing with its shaft horizontal, how can I cause its shaft to lift so that it becomes tilted upwards at an angle ψ as shown on the right? I push the shaft round horizontally in the direction in which it is precessing. As I do so, the shaft tilts upwards by revolving around the support point in a direction perpendicular to that in which I push it.
Now let us revert to considering the whole fly-wheel disc: not just a single sink hole on its outer rim. How can I cause a spinning fly-wheel to adopt this tilted mode of precession? Starting with the fly-wheel disc precessing with its shaft horizontal, how can I cause its shaft to lift so that it becomes tilted upwards at an angle ψ as shown on the right? I push the shaft round horizontally in the direction in which it is precessing. As I do so, the shaft tilts upwards by revolving around the support point in a direction perpendicular to that in which I push it.
What I am thereby doing is applying a torque in the horizontal plane: I supply one half of the torque's force-couple by pushing on the shaft, the other half-couple being the horizontal reaction of the support stand.
I could do this by accelerating the support stand horizontally by applying a horizontal linear force to it. Notwithstanding, I only get the impression of my finger [or whatever] exerting a linear force because it is only exerted for about 200 milliseconds or so. Strictly, as I exert the force, I must follow a short arc having the same radius as the orbit of precession. To be pedantic, the short arc is a very short spiral section whose starting radius is the radius of precession when the fly-wheel's shaft is horizontal and whose final radius is the radius of precession when the fly-wheel's shaft has achieved its final tilt. Hence: no real linear force is involved. Hence it is a torque: not a linear force. [Don't worry about this.]
To achieve a permanent tilt angle of ψ to the horizontal, I apply this horizontal torque to the support stand for only a small amount of time.
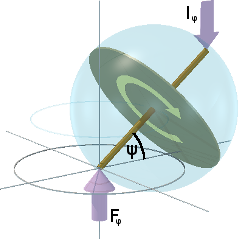 The surprise is that the torque that needs to be exerted to elevate the fly-wheel is very small compared with the would-be dead weight W of the fly-wheel. The upward force Fψ exerted on the tilted shaft is greater than the upward force F0 was when the shaft were horizontal. Notwithstanding, it is still not equal to the dead weight W of the fly-wheel. I would guess that the ratio between W, Fψ and F0 somehow involves the cosine of the angle ψ. If I push the shaft in the direction of precession until it becomes vertical (ψ=½π), the upward force F½π on the support becomes the dead weight W of the fly-wheel.
The surprise is that the torque that needs to be exerted to elevate the fly-wheel is very small compared with the would-be dead weight W of the fly-wheel. The upward force Fψ exerted on the tilted shaft is greater than the upward force F0 was when the shaft were horizontal. Notwithstanding, it is still not equal to the dead weight W of the fly-wheel. I would guess that the ratio between W, Fψ and F0 somehow involves the cosine of the angle ψ. If I push the shaft in the direction of precession until it becomes vertical (ψ=½π), the upward force F½π on the support becomes the dead weight W of the fly-wheel.
It seems also that the fly-wheel's inertia is now more apparent. The inertial reaction Iψ is equal and opposite to the force Fψ, consequently, the inertia Iψ of the tilted fly-wheel is greater than the inertia I0 of the fly-wheel when its shaft is horizontal. It must then follow that the mass mψ of the fly-wheel when its shaft is tilted must be greater than the mass m0 of the fly-wheel when its shaft is horizontal. And in turn, the static mass m½π (what is conventionally perceived as the mass) of the fly-wheel must be greater than the mass mψ of the fly-wheel when its shaft is tilted.
Notwithstanding, to say that the mass of the fly-wheel varies does not give the complete picture. The mass of the fly-wheel, within the present context, is not a universal thing. It is the fly-wheel's apparent mass from the point of view of the applied force F. For this reason, perhaps it is better to imagine the rotating fly-wheel to be of fixed orientation and to imagine the support stand (or rocket) to be tilted with respect to the fly-wheel's shaft. Then, from the point at the end of the shaft, the mass of the fly-wheel varies with the direction of the applied force.
The consequence of this observation is that mass cannot be a mere scalar quantity pertaining to the fly-wheel. It must be a vector field pertaining to the fly-wheel's relationship with the applied force. And the conduit of that relationship is the asymmetry in the æthereal flux, flowing into all the sink holes of the fly-wheel, caused by the application of the force.
In the previous two illustrations, I have shown the fly-wheel and its shaft enclosed inside a translucent sphere. This is firstly to show that the length of the fly-wheel's half-shaft is equal to that of its radius. Pretty well all gyroscope fly-wheel units are built to this proportion. It seems that when the half-shaft length is equal to the fly-wheel's radius, the gyroscopic effect is at its maximum, although I am not entirely sure about this. Secondly, the translucent sphere is a useful construct for considering how the apparent mass of the fly-wheel varies with direction.
Envelope of Precession
 Imagine the fly-wheel back in free space. The support stand is a rocket. If the fly-wheel is not rotating or precessing, the force F required to accelerate it at a fixed rate a is given by the equation F=m×a, where m is the mass of the fly-wheel. If it is rotating and precessing, the equation must be qualified with the subscript ψ viz. Fψ=mψ×a because the mass mψ of the fly-wheel decreases as the angle ψ increases. Consequently, the force Fψ necessary to keep the fly-wheel accelerating at a constant rate of a must decrease as the angle ψ increases.
Imagine the fly-wheel back in free space. The support stand is a rocket. If the fly-wheel is not rotating or precessing, the force F required to accelerate it at a fixed rate a is given by the equation F=m×a, where m is the mass of the fly-wheel. If it is rotating and precessing, the equation must be qualified with the subscript ψ viz. Fψ=mψ×a because the mass mψ of the fly-wheel decreases as the angle ψ increases. Consequently, the force Fψ necessary to keep the fly-wheel accelerating at a constant rate of a must decrease as the angle ψ increases.
I wager that for an ideal fly-wheel, its mass varies as the cosine of the angle ψ such that mψ=m0×cos(ψ), where m0 is the dead-mass of the fly-wheel. Here I define an ideal fly-wheel as having all its substance concentrated into an infinitely thin layer on its rim held by a weightless disc and half-shaft. The variable force Fψ required to keep the fly-wheel accelerating at a constant rate of a metres per second per second would then be given by Fψ=m0×cos(ψ)×a.
When the length L of the fly-wheel's half-shaft is greater or less than the radius R of the fly-wheel, the circular function cos(ψ) would become an elliptical function e.cos(ψ). In this sense, the circular function cos(ψ) [where L = R] is really a special case of e.cos(ψ) [where L ≶ R].
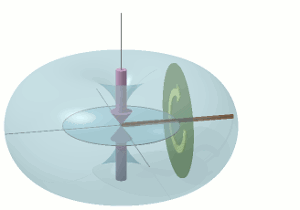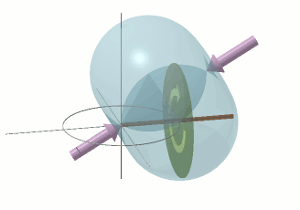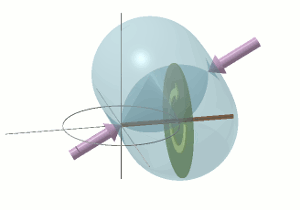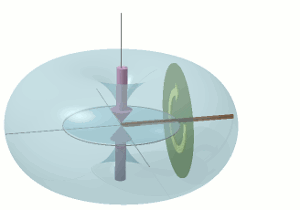 The size, shape and orientation of the envelope, defining the limit of the fly-wheel's excursions within its orbit of precession, varies with the angle ψ at which the force Fψ is applied to one end of the fly-wheel's shaft. The way in which this envelope varies is illustrated in the animation on the left. The shape of the envelope varies from a horn torus (when ψ = 0) to a sphere (when ψ = ½π). The major and minor radii of the torus are both equal to the radius R of the sphere.
The size, shape and orientation of the envelope, defining the limit of the fly-wheel's excursions within its orbit of precession, varies with the angle ψ at which the force Fψ is applied to one end of the fly-wheel's shaft. The way in which this envelope varies is illustrated in the animation on the left. The shape of the envelope varies from a horn torus (when ψ = 0) to a sphere (when ψ = ½π). The major and minor radii of the torus are both equal to the radius R of the sphere.
NOTE: A horn torus is a torus whose minor radius is equal to its major radius such that the would-be passage through its centre is only just at its point of closure, somewhat like the normal state of the anal sphincter.
When the angle ψ is zero, the half-shaft of the precessing fly-wheel sweeps out a disc, shown as a darker shade of translucent blue in the above animation. As ψ increases, the disc gradually closes into a cone of ever-decreasing angle until it closes completely onto the fly-wheel's shaft. At all values of ψ (between 0 and 90°) the cone represents the surface swept by the half-shaft of the precessing fly-wheel.
The lower conical arrow represents the real directed force Fψ exerted at the end of the fly-wheel's half-shaft. The upper conical arrow represents the equal and opposite inertial reaction Iψ to the force. The distance between the points of the two arrows is, for every value of ψ, proportional to the magnitude of the force Fψ required to keep the fly-wheel accelerating at a metres per second per second. This distance is also the distance between the two cusps at which the diametrically opposite parts of the torus overlap and encroach into each other. This situation is where the major radius of the torus is actually less than its minor radius R.
NOTE: The foregoing assumes an ideal fly-wheel, as previously defined. Any real rotating object will invariably have a component of what I shall term dead-mass. This is essentially that part of the body which is either not rotating, or not rotating sufficiently, to be completely within the gyroscopic state.
In the real world — or perhaps I should say: the real universe — rotating objects are never perfect fly-wheels. Most rotating objects, I would guess, are more of a spherical or oblate ellipsoidal shape. A real directed force can be applied only at one of the two points, on the surface of such an object, through which its axis of rotation passes. These points correspond to the ends of a fly-wheel's shaft. On the macroscopic scale — the scale of stars and planets — the object itself can be seen and observed. On the microscopic scale — the scale of fundamental particles — the object cannot be seen or observed. If such a particle contained an internal rotating component, the most we could detect would be its acceleration, applied force and hence its apparent mass. We would be unaware of what was going on inside it.
 To any human observer, such a particle can only be the envelope of precession of whatever rotating element is inside it. Such a particle could possibly exhibit quite a wide range of what is conventionally perceived as mass. But whereas it exhibits its minimum "mass" along any convergent radial lying within a (2-dimensional) plane, it exhibits its maximum "mass" only directly along a single (1-dimensional) line. And it exhibits intermediate values of "mass" along an infinite series of conical surfaces.
To any human observer, such a particle can only be the envelope of precession of whatever rotating element is inside it. Such a particle could possibly exhibit quite a wide range of what is conventionally perceived as mass. But whereas it exhibits its minimum "mass" along any convergent radial lying within a (2-dimensional) plane, it exhibits its maximum "mass" only directly along a single (1-dimensional) line. And it exhibits intermediate values of "mass" along an infinite series of conical surfaces.
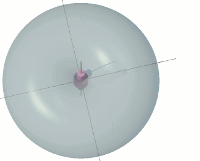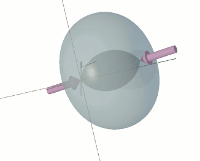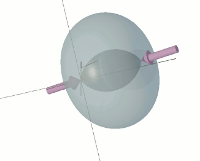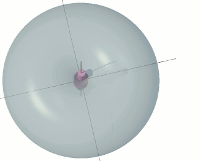 Therefore, the situations in which the particle exhibits its dead-weight mass to an applied force are very rare compared with those in which it exhibits very little mass. A particle can only be detected by somehow applying an external real directed force to it and observing its reaction to that applied force. Thus, a single entity of this kind will inevitably appear as any one of a continuum of particles of different masses and shapes according to the relative direction from which a force is applied to it.
Therefore, the situations in which the particle exhibits its dead-weight mass to an applied force are very rare compared with those in which it exhibits very little mass. A particle can only be detected by somehow applying an external real directed force to it and observing its reaction to that applied force. Thus, a single entity of this kind will inevitably appear as any one of a continuum of particles of different masses and shapes according to the relative direction from which a force is applied to it.
For any given direction ψ of an applied force, the envelope, of a rotating precessing object, could be thought of as the probability shell enclosing the space within which the rotating precessing object could be anywhere at any given instant. To me, this is loosely analogous to the notion of the probability shell of an electron within an atom. I think it would be interesting to investigate whether or not the envelope of a rotating precessing entity could possibly give rise to established observations of the nanoscopic world.
Mechanism of "Mass-Loss"
The means whereby the fly-wheel produces a torque, which acts in the sense necessary to support it from one end of its shaft, has already been established. Notwithstanding, a very big problem remains. The amount of inertial reaction, generated by this torque, acting upon the support stand, is extremely small compared with that which would be necessary to cantilever the entire dead-weight of the fly-wheel. The small magnitude of this inertial reaction suggests that it is cantilevering the weight w of a much smaller mass m than the mass M required to account for the dead-weight W of the fly-wheel.
If one believes in mass as a property of matter then there are only two possibilities: either the fly-wheel's mass has become drastically reduced, or, it has, for the most part, become hidden from the observer's world. On the other hand, if one thinks of mass as a manifestation of the fly-wheel's relationship with the rest of the universe, there is another option for explaining the smallness of the inertial reaction which the end of the fly-wheel's shaft exerts upon the support stand. This is to consider how the profile of the æthereal flux density, for a sink hole on the rim of the fly-wheel, varies as it revolves around the fly-wheel's centre of rotation.
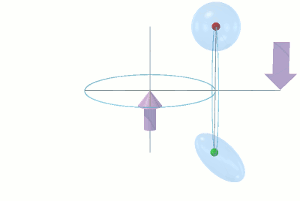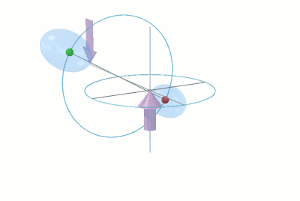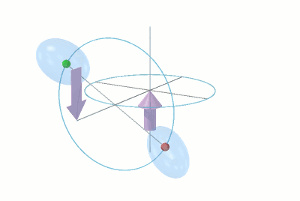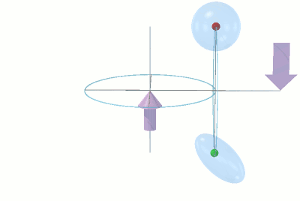 The animation on the right is a repeat of the earlier animation showing two diametrically opposite sink holes on the rim of a fly-wheel whose angular velocity of rotation ω is the same as its angular velocity of precession Ω. In this animation, however, a contour of constant æthereal flux density (shown in translucent blue) has been added for each of the two sink holes. Please notice how each sink hole's contour of constant flux density changes shape as it revolves around the axis of the fly-wheel.
The animation on the right is a repeat of the earlier animation showing two diametrically opposite sink holes on the rim of a fly-wheel whose angular velocity of rotation ω is the same as its angular velocity of precession Ω. In this animation, however, a contour of constant æthereal flux density (shown in translucent blue) has been added for each of the two sink holes. Please notice how each sink hole's contour of constant flux density changes shape as it revolves around the axis of the fly-wheel.
As a sink hole passes the uppermost point, its contour of constant flux density is spherical. As it passes the lowest point, its contour of constant flux density is at its most prolate. The orientation of the major axis of the prolate ellipsoidal contour of constant flux density lies along a line from the point of the support stand. The direction of minimum flux density gradient lies along this line in the direction away from the support point.
As a sink hole descends from the uppermost point, its contour of constant flux density starts off spherical and becomes more and more prolate until it reaches the lowest point. As the sink hole subsequently ascends from the lowest point, its contour of constant flux density becomes less and less prolate until it once again becomes spherical at the top. But why does it do this?
 In the animation, I made Ω = ω. Consequently, each time a sink hole passes the uppermost point, it isn't actually revolving around anything. It is completely stationary with respect to the support point. This leaves the radial in-flow of its æthereal flux spherically symmetrical. Thus, the æthereal flux density gradient, at any given radial distance from the sink hole, is the same in all directions.
In the animation, I made Ω = ω. Consequently, each time a sink hole passes the uppermost point, it isn't actually revolving around anything. It is completely stationary with respect to the support point. This leaves the radial in-flow of its æthereal flux spherically symmetrical. Thus, the æthereal flux density gradient, at any given radial distance from the sink hole, is the same in all directions.
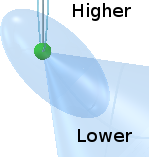 Conversely, each time a sink hole passes the lowest point, it is moving at its maximum angular velocity 2Ω around the axis of the fly-wheel. As a result of the centrifugal inertial reaction thus generated, the radial in-flow of its æthereal flux is at its most asymmetrical. Thus, the æthereal flux density gradient, at any given radial distance from the sink hole, is different in different directions. Specifically, in all but a small solid angle of directions, the æthereal flux density gradient is, in this case, very much higher.
Conversely, each time a sink hole passes the lowest point, it is moving at its maximum angular velocity 2Ω around the axis of the fly-wheel. As a result of the centrifugal inertial reaction thus generated, the radial in-flow of its æthereal flux is at its most asymmetrical. Thus, the æthereal flux density gradient, at any given radial distance from the sink hole, is different in different directions. Specifically, in all but a small solid angle of directions, the æthereal flux density gradient is, in this case, very much higher.
More importantly, however, within the small solid angle centred on the sink hole and enclosing the outward radial, the æthereal flux density gradient is very much reduced. This means that, from the point of view of an observer who is further than the sink hole from the centre of the fly-wheel, the apparent mass of the sink hole is very much reduced. In other words, it appears to be a lot less than unity.
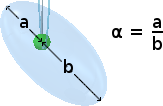 Consequently, the inertial reaction I of the sink hole to any real directed force, applied in the upward direction, is significantly less. In effect, from the point of view of this force, my universal constant, which I have previously called k, is effectively multiplied by the asymmetry ratio α of the outward to inward radial flux density gradients. The ratio α is of course fractional.
Consequently, the inertial reaction I of the sink hole to any real directed force, applied in the upward direction, is significantly less. In effect, from the point of view of this force, my universal constant, which I have previously called k, is effectively multiplied by the asymmetry ratio α of the outward to inward radial flux density gradients. The ratio α is of course fractional.
Consider the rotating precessing fly-wheel to be precessing around its support stand in Earth's gravity. Since ω=Ω, the combined precession rate of 2Ω resolves as a revolution of the sink hole around the point of the support stand. So, because the length of the fly-wheel's half-shaft is equal to the radius of the fly-wheel, the radius of revolution joining the sink hole and the point of the support stand is at 45° to the horizontal (or the vertical). Hence, the prolate ellipsoidal contours of constant flux density gradient is inclined at 45°, as shown in the above animation and the subsequent diagrams.
 The proportional weight loss of the fly-wheel is the same as its "mass loss" ratio α in the upward vertical direction. So the relevant value of α is the ratio a:b where a and b are measured along the vertical radial of the fly-wheel as shown on the right. Of course, this only applies when the sink hole is at the bottom of the fly-wheel. The value of α for all the sink holes at all other places within the material of the fly-wheel must be greater.
The proportional weight loss of the fly-wheel is the same as its "mass loss" ratio α in the upward vertical direction. So the relevant value of α is the ratio a:b where a and b are measured along the vertical radial of the fly-wheel as shown on the right. Of course, this only applies when the sink hole is at the bottom of the fly-wheel. The value of α for all the sink holes at all other places within the material of the fly-wheel must be greater.
Consequently, the combined "mass-loss" of the fly-wheel as a whole can only be arrived at by a rather complicated process of integration, which must take into account the varying contributions of ω and Ω for all the different radii and angular positions at which each sink hole, within the material of the fly-wheel, lies.
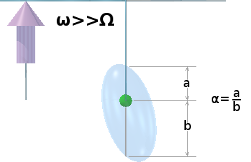 As can be seen from the above diagram, when ω=Ω (when the prolate ellipsoidal contour of constant flux density lies at 45° to the vertical), the distances a and b are not very different. So α is a fairly large fraction. Consequently, the effective "mass-loss" of the fly-wheel is not very great. However, if we rev up the fly-wheel to make ω very much greater than Ω, the contour tilts much more towards the vertical, making α a much smaller fraction.
As can be seen from the above diagram, when ω=Ω (when the prolate ellipsoidal contour of constant flux density lies at 45° to the vertical), the distances a and b are not very different. So α is a fairly large fraction. Consequently, the effective "mass-loss" of the fly-wheel is not very great. However, if we rev up the fly-wheel to make ω very much greater than Ω, the contour tilts much more towards the vertical, making α a much smaller fraction.
This has the effect of reducing the apparent mass of the fly-wheel — and hence its weight — to a much greater extent. This, in turn, correspondingly reduces the upward force, which the support point must exert upon the end of the half-shaft, in order to support the rotating precessing fly-wheel.
A Self-Regulating State
A fly-wheel, which is rotating and precessing at smooth constant angular velocities (ω and Ω), is in a stable dynamic state. This stable dynamic state is an attractor. This means that, should the fly-wheel be perturbed from this smooth constant dynamic state by some external influence, it will automatically gravitate back to its original smooth constant dynamic state. In so doing, the rotating precessing fly-wheel will dissipate, into its environment, any energy it received from whatever perturbed it.
Perturbing the fly-wheel momentarily, in its direction of spin, causes its angular velocity of rotation ω to increase. However, this results in a corresponding reduction in its angular velocity of precession Ω, such that its overall angular momentum of rotation plus precession does not change. So there is no change in its overall energy. The perturbing pulse, in this case, is met by very little inertial reaction.
Perturbing the fly-wheel momentarily, in its direction of precession, causes the fly-wheel to move to an inclined orbit (ψ>0). This, in turn, produces a corresponding increase in the downward inertial reaction exerted by the end of the fly-wheel's half-shaft upon the support stand. Although this results in an increase in the fly-wheel's so-called potential energy (which is relative), it does not impart any absolute energy to the fly-wheel's rotating precessing state. The perturbing pulse, in this case, is also met by very little inertial reaction.
Notwithstanding, any attempt to momentarily perturb the fly-wheel in the direction perpendicular to both its spin and its precession is met with a very strong inertial reaction. This inertial reaction is truly a reactance and not a resistance. In other words, it does not, itself, directly dissipate the energy of the perturbing impulse. Rather, it stores the energy imparted by the impulse. And it stores this energy in the dynamic form of a mechanical oscillation. This form of mechanical oscillation is called nutation.
 The phenomenon of nutation is illustrated by the adjacent animation. A perturbing pulse is momentarily applied downwards at the free end of the shaft. This produces an instantaneous increase of δΩ in the fly-wheel's angular velocity of precession. So the fly-wheel is now precessing at an angular velocity of Ω + δΩ. This new angular velocity of precession is now too fast for the horizontal orbit to be stable.
The phenomenon of nutation is illustrated by the adjacent animation. A perturbing pulse is momentarily applied downwards at the free end of the shaft. This produces an instantaneous increase of δΩ in the fly-wheel's angular velocity of precession. So the fly-wheel is now precessing at an angular velocity of Ω + δΩ. This new angular velocity of precession is now too fast for the horizontal orbit to be stable.
NOTE: In this discussion, I assume that the fly-wheel precesses round a support stand in Earth's gravity. However, it could equally well be in free space, away from the influence of any other objects, with the support stand replaced by a rocket. The rocket maintains a thrust F to sustain the precession of the fly-wheel, which is countered by an equal and opposite inertial reaction I from the fly-wheel. The momentary pulse is provided by an extra short sharp burst of thrust δF from the rocket, which is countered by an equal and opposite inertial pulse δI from the fly-wheel.
This increase δΩ in the fly-wheel's velocity of precession creates a corresponding increase δτs in the upward torque on the fly-wheel. However, the externally-applied downward pulse is short-lived. When it finishes, the fly-wheel's angular velocity of precession drops instantly back to Ω. Notwithstanding, the increase in torque δτs, which has now disappeared, has imparted an upward angular momentum to the fly-wheel. Consequently, the fly-wheel is now travelling upwards, away from its stable horizontal orbit of precession.
Having insufficient angular velocity of precession to maintain a higher orbit, the fly-wheel eventually loses all its upward momentum and falls back down again to its stable orbit. However, as it passes its stable orbit again, it has the reverse of its original upward momentum supplied by the short-lived additional upward torque δτs. Consequently, the fly-wheel overshoots its stable orbit in a similar way to that in which a pendulum overshoots its vertical rest position. The fly-wheel therefore continues downwards to a lower orbit for which its angular velocity of precession Ω is again inadequate. So the fly-wheel starts to "fall" upwards back towards its stable horizontal orbit. This process repeats, with the fly-wheel oscillating (nutating) upwards and downwards, above and below its stable horizontal orbit, in what appears ostensibly to be a sinusoidal motion.
To illustrate this motion clearly, the above animation shows this oscillation as indefinitely sustained. In reality, however, the oscillatory motion of nutation is heavily damped. It decays rapidly, with the fly-wheel quickly reverting to its original smooth stable state of continuous precession around its horizontal orbit. In this sense, it is less of the nature of a swinging pendulum and more like the audible ring of a bell or the damped oscillation of a resonant electrical circuit containing a large element of pure resistance. This rapid damping is, in effect, the necessary negative feed-back mechanism that pulls the perturbed fly-wheel back to its original stable dynamic state.
The energy, of the original perturbing pulse, is thus dissipated quite rapidly by the process of nutation. To my mind, this rate of damping cannot be accounted for by friction alone. In fact, I think that mechanical friction can account for only very little of the damping that occurs. Consequently, most of the energy, delivered by the original perturbing pulse, must be dissipated by some other mechanism, which is clearly not thermal nor any other kind of electromagnetic radiation.
This suggests to me that the impedance, which damps the nutational oscillation, must be more reactive than resistive. In other words, the process of nutation does not, itself, dissipate the energy but, instead, converts the energy into some other form. Since this energy is not readily perceivable by human sense or instrument, I am led to believe that it must be radiated as an æthereal flux-density wave. It effectively modulates the density-gradient of the flux of the passing æther which is flowing into every sink hole in the universe.
The momentary pulse causes sink holes in the fly-wheel to accelerate in directions perpendicular to the plane of the fly-wheel. This causes an elongation in the contours of constant flux-density surrounding each sink hole. This, in turn, causes a momentary shift in the magnitude and direction of the flux density gradient surrounding the sink hole, which gives rise to a radiating æthereal flux density pulse, which effectively radiates away from the sink hole.
A pulse of such modulation occurs whenever the fly-wheel is momentarily perturbed from any stable orbit. And this is true not only for the orbit in which the fly-wheel's shaft is horizontal (perpendicular to the force exerted by the support stand) but for all orbits at any inclination ψ to the horizontal.
Forced Rotation
The following diagram is big because it is important for it to show clearly what exactly is going on here.
The fly-wheel and its shaft have been already revved up and are rotating at an angular velocity ω. The fly-wheel thus already has considerable rotational energy and momentum. Assuming the fly-wheel mountings to be frictionless, this rotational energy and momentum should not diminish with time.
The force-couple F, acting at a radius R around the axial origin, has precisely the amount of force-moment required to suppress any attempt by the fly-wheel to precess around the y-axis. This could be done by a clamping gimbal that allows rotation only in the plane of the torque τ. Perhaps a scientifically neater way would be to mount two contra-rotating fly-wheels side-by-side in a rigid frame structure.

The torque τ is strong. It forcibly rotates the fly-wheel around the z-axis. However, in so doing, it is met by what appears to be an opposing torque of equal magnitude. Also, doing this appears to sap rotational energy from the fly-wheel. The fly-wheel seems to suffer some kind of breaking torque applied to it in its plane of rotation.
Applying a torque through an angle expends energy, as does applying a force over a distance. Thus we have expended energy in applying the torque τ. We have also sapped at least some of the fly-wheel's rotational energy.
Notwithstanding, none of this works in reverse. If we rev up the fly-wheel to angular velocity ω, no torque −τ appears. And changing the direction of spin that we apply to the fly-wheel alters nothing. If we apply the torque τ without the fly-wheel spinning, allowing the torque to act over many revolutions, it only accelerates the fly-wheel to rotate about the z-axis with little inertial opposition compared with when the fly-wheel is spinning.
Consequently two [ostensibly equal] amounts of energy have been expended: one in revving up the fly-wheel in the first place and another in applying the torque τ at angular velocity Ω [in the sense shown in the above diagram] that killed the angular velocity ω of the fly-wheel.
The phenomenon appears only when the torque τ does work by rotating through an angle while the fly-wheel is supplying a separate source of rotational energy.
Furthermore, the irreversibility of this process of energy transfer verifies that one source of energy hasn't simply cancelled the other by working in opposition to it. If the two energies were opposing each other, the process would be reversible or the apparatus would dissipate heat. But the process isn't reversible and the fly-wheel doesn't heat up. So where have these two lots of energy gone?
The situation here is somewhat similar to that when you apply a torque to a fly-wheel precessing round a support stand at the end of its half-shaft. If you apply the torque in the direction of precession, the fly-wheel rises to a smaller upwardly-inclined orbit. In so doing, you expend energy. If you then apply the same torque for the same amount of time contrary to the direction of precession, the fly-wheel descends back to its original orbit. In so doing, you have expended another equal amount of energy. Where have these two equal amounts of energy gone?
The above experiment could be enhanced by integrating an electric motor into the fly-wheel with an electronic controller that maintains the angular velocity ω despite large variations of loading torque. Also, a synchronous [or stepping] motor could be used to apply the torque τ with a constant angular velocity Ω. Both motors would consume electricity at constant rates. In other words, they would be consuming a constant power [in watts].
The motors will naturally heat up because they are not 100% efficient in converting electrical power into rotational mechanical power. However, the heat dissipated will not account for anything approaching the power consumption of the motors. Most of the electrical power consumption is going somewhere else. I would wager that it must be being emitted as some kind of 'inertial' radiation.
It seems that we have here a rotational counterpart of what I described in my essay Force & Inertia about the energy expended by a linear force, acting against an inertial reaction over a distance, to accelerate an object. The object does not itself dissipate the energy expended by the force but acts as a transducer, which radiates the energy as an inertial wave. There, I established my conjecture that mass be simply a kind of coefficient of inertia, which is not a property of the object itself, but rather, a property of the object's relationship with the 'fabric' of space-time.
At this point, we have, in this essay, considered 4 situations:
A linear force, applied to an object, causes that object to undergo a linear acceleration, which is proportional to the object's mass. This linear force is opposed by an equal and opposite inertial reaction.
A force-couple, applied ostensibly at the ends of the shaft of a spinning fly-wheel, which results in the fly-wheel precessing in the plane perpendicular to the applied force-couple. The force-couple comprises an upward force applied by a central pivot stand at one end of the fly-wheel's half-shaft which is complemented by the 'weight' of the fly-wheel.
A torque, applied to a non-spinning fly-wheel, causes the fly-wheel to rotate with an accelerating angular velocity, which is proportional to the fly-wheel's angular inertia, which, in turn, depends on both its mass and its particular axis of rotation. Likewise, the torque is opposed by an equal reactive inertial torque.
A torque, applied around a diameter of a precession-suppressed spinning fly-wheel, causes the fly-wheel to rotate with a constant angular velocity, which is proportional to the fly-wheel's angular inertia, which, in turn, is proportional to the fly-wheel's mass and rate of spin. Likewise, the torque is opposed by an equal reactive inertial torque.
Situation 'C' above is clearly the rotational counterpart of Situation 'A'. In other words, Situation 'C' is to rotational motion as Situation 'A' is to linear motion. Notwithstanding, Situation 'D' is very different from Situation 'C' for 3 reasons.
In Situation 'C' the torque causes angular acceleration whereas in Situation 'D' the torque can only attain a constant angular velocity.
The magnitude of the inertial reaction against the torque in Situation 'D' is vastly greater than that in Situation 'C'.
In Situation 'D' only, the applied torque seems to be opposed not only by the static inertia of the fly-wheel's mass, but also — and vastly more so — by the rotational energy within the fly-wheel's spin.
Through some additional, invisible, mysterious form of coupling. It is as if the torque applied in Situation 'D' has the same effect on the fly-wheel's rotation as the caliper has on the disc brake on a car wheel, except that the latter dissipates the rotational energy as heat, whereas the former doesn't. So, again, in the former case, where does the energy go?
Non-Reversibility
It is extremely important to note that in all four of the above situations, the process is non-reversible.
In Situation 'A', an inertial reaction cannot spontaneously cause an object to exert a force — thereby causing itself to accelerate or to push against another object. Likewise, in Situation 'B', a fly-wheel spinning in free space will not spontaneously start to precess and thereby exert a force-couple at the ends of its half-shafts in a plane perpendicular to its precession. In Situation 'C', a non-spinning fly-wheel will never spontaneously start to spin with an accelerating angular velocity about a diameter and thereby exert a torque around that diameter. In Situation 'D', a gimbal-clamped spinning fly-wheel will not spontaneously rotate about a diameter, thereby creating a torque around that diameter.
This non-reversibility strongly suggests that each of these four situations involves a process that results in an increase in entropy. In other words, a concentrated cause becomes a dispersed effect. The most obvious conclusion is that the linear or rotational action becomes transmuted into a wave: in this case, an inertial wave.
A poignant corollary to the above is that the application of a torque to any form of gyroscopic mechanism cannot generate a resultant linear force.
Inertial Coupling
I referred above to my conjecture that mass be simply a kind of coefficient of inertia, which is not a property of the object itself, but rather, a property of the object's relationship with the 'fabric' of space-time. The fact that there even exists an inertial reaction to a force applied to an object suggests — nay, mandates — that there must be some kind of reactive coupling between matter and space.
Furthermore, it would appear that, in the case of rotation, there are 2 kinds of such coupling, which are quite separate and distinct from each other: the second being a vastly stronger effect than the first.
Situation 'A' above is when a linear force f is applied to an object of mass m, causing it to accelerate at a metres per second per second. Here, for any given magnitude of the force f, the resulting amount of acceleration per unit mass is a constant, as given by Newton's Law f = m × a. The units of measure are scaled such that any implied constant of proportionality is 1 [unity]. We could be pedantic and put in a constant of proportionality in Newton's formula: f = Я × m × a, where, for Situation 'A': Я = 1.
In this series of essays, I have already used various Greek and Hebrew letters to represent the new universal constants that I have concocted. So here I decided to make a bit of a change and use the Russian letter Я, which, as I am given to understand, is pronounced "ya".
Situation 'B' is when a spinning fly-wheel is precessing around a support at the end of one of its half-shafts under normal Earth gravity. The upward force f is very much less than the dead-weight of the fly-wheel.
I remember a video in which Professor Eric Laithwaite spun up a 40 pound [18 kilogram] fly-wheel to 2500 revolutions per minute. He then lifted it up above his head, by the free end of its shaft, with only one hand while allowing it to precess around him. He was quite old at the time [1983] and he said it felt "as light as a feather". Consequently, I would estimate the upward force he was exerting to be no more than about a tenth of its dead-weight [i.e. 1·8 kg]. When weighing the fly-wheel before spinning it up, it took him a lot of effort to lift it a few centimetres off the floor.
So it would seem that, in Situation 'B', the value of Я in my augmented version of Newton's Law would be around 0·1. In other words, the inertial coupling between the object and free space for a precessing fly-wheel, for a force applied at the cusp of the 'anal sphincter', is about a tenth. Of course, as the angle between the force and the plane of the fly-wheel increases, this coefficient of inertial coupling would vary from a tenth up to unity. That is: as 0 ≤ ψ ≤ ½π, so 0·1 ≤ Я ≤ 1.
Situation 'C' is where a torque, which acts around a diameter of a non-spinning fly-wheel, causes the fly-wheel to rotate with an accelerating angular velocity. It obeys a rotational version of Newton's Law: τ = Я × M × Ω', where Я = 1 and Ω' ≡ dΩ/dt. However, here, M isn't simply the 'mass' of the fly-wheel as such. It is the inertial moment of the fly-wheel about an axis through any diameter of the fly-wheel.
Situation 'D' is where a torque, applied around a diameter of a precession-clamped spinning fly-wheel, causes the fly-wheel to rotate with a constant angular velocity. This doesn't follow Newton's Law. It follows the law: τ = Я × M × Ω. However, in this case, from direct observation, Я seems to be about 10 times what it was in Situation (C). So it would seem that material revolving about two mutually perpendicular axes at the same time has a much tighter coupling with the 'fabric' of space. It invokes the notion that perhaps its mechanical impedance matching to free space is at, or at least much closer to, perfect resonance.
Compare the Situations
In Situation 'A' a force and in Situation 'C' a torque work against corresponding inertial reactions, thereby giving rise respectively to constant linear & angular accelerations. They both consume power but do not dissipate it: they transduce it. They simply accelerate 'mass': 'A' in a straight line and 'C' in a circle. They obey the augmented Law of Newton: f = Я × m × a, where Я = 1. They really don't involve the gyroscopic phenomenon.
Situations 'B' & 'D' are very different from Situations 'A' & 'C'. They both involve the somewhat enigmatic gyroscopic phenomenon.
Situations 'B' & 'D' both operate at constant velocity instead of constant acceleration. In other words, they seem to operate at one order of differentiation [with respect to time] less than Situations 'A' & 'C'. Also, they are the only ones that involve circular motion that is perpendicular to the plane of spin of a spinning fly-wheel.
In Situation 'B' a force-couple gives rise to reactionless precession.
Situation 'B' is the same as Situation 'D' except that the fly-wheel is free to precess and that consequently the anticipated inertial reaction to the applied torque seems to be 'side-stepped'. Situation 'B' is the only one of the 4 situations, which, at first sight, does not appear to be dissipative: it seems to consume no power. Consequently, the precessing fly-wheel appears to be in a state of dynamic rest or equilibrium with respect to the rest of the universe. But perhaps this is not quite as it seems.
In Situation 'D' a very strong torque gives rise to an equally strong inertial reaction. Situation 'D' is the same as Situation 'B' except that precession is forced further by an applied torque or force-couple and the tendency for the shaft of the fly-wheel to tilt upwards to a smaller and higher orbit is forcibly suppressed. Unlike Situation 'B', however, Situation 'D' is dissipative. It consumes power: in fact, vastly more so per unit 'mass' of the object in Situation 'A' or of the fly-wheel in Situation 'C'. It seems to be a mechanism that makes a far more direct and intimate coupling between the fly-wheel assembly and the very 'fabric' of space.
The Dynamic Geometry
I established my conjecture, in my essay on Force & Inertia, that a body accelerated by a force transduces the energy expended by that force, as it works against the inertial reaction, into an inertial wave.
 Let's look again at Situation 'B' viz: two sink-holes on the rim of a fly-wheel that is precessing around a central pivoted support at the free end of one of its half-shafts. Stare at the green sink-hole and follow it carefully around its composite orbit: its revolution + precession combined to form a single larger orbit. Notice that the speed of the sink-hole as it travels this composite orbit is not constant.
Let's look again at Situation 'B' viz: two sink-holes on the rim of a fly-wheel that is precessing around a central pivoted support at the free end of one of its half-shafts. Stare at the green sink-hole and follow it carefully around its composite orbit: its revolution + precession combined to form a single larger orbit. Notice that the speed of the sink-hole as it travels this composite orbit is not constant.
Notice also that the orbit is not truly circular. It follows a kind of munted circle a bit like a bicycle wheel that has been buckled asymmetrically in a road accident. I don't know any mathematical name for such a shape, if indeed there be one.
Note: as the animation demonstrates, the path speed of the composite orbit cannot be resolved as the simple vector sum of the two mutually perpendicular orbits of constant-path-speed.
When the sink-hole passes the bottom-front of its composite orbit, it is travelling at 2 × R × ω metres per second whereas, as it passes the upper rear of its orbit, its orbital speed is zero. So, as it travels from the upper rear to the lower front of its orbit, it accelerates from zero to 2Rω metres per second, while during the second half of its composite orbit, it decelerates from 2Rω back down to zero metres per second. Thus, in Situation 'B', every part of the fly-wheel's material is all the time in a state of acceleration.
Note that in terms of universal free space, deceleration [negative acceleration] is simply acceleration in the opposite direction. It is in principle the same as acceleration: undergoing a change of track speed with time.
At this point, I feel it necessary to digress slightly to untangle a potential conceptual problem. Velocity is defined as speed in a straight line, while speed is simply a rate at which an object passes along a track — irrespective of how straight, bent or convoluted that track may be. Notwithstanding, this view of velocity and speed is a legacy of our Earth-bound conceptual upbringing. In the universal context, we need to define velocity as the track-speed an object has while travelling along a 'world-line'. That is, while it is not being acted upon by any directed externally applied force acting at a point on its surface.
NOTE: An inertial reaction is not a force. An inertial reaction is provoked by a directed externally applied force: but a directed externally applied force can't be provoked by an inertial reaction. A force and its corresponding inertial reaction aren't interchangeable. They aren't reversible.
A so-called 'centrifugal force' [a force that appears to act radially outwards from the axis of a rotating fly-wheel] is not a force: it is an inertial reaction. A centripetal force is the real force that provokes an inertial reaction erroneously called a "centrifugal force". Consequently, a "centrifugal force" cannot accelerate outwards the material on the periphery of a rotating fly-wheel. If the fly-wheel shatters, the liberated material moves tangentially from the rest of the fly-wheel: not radially.
What I have been trying to establish in my digression here is that acceleration, in the sense of what provokes an inertial reaction, is rate of change of speed along a track — whether that track be straight, circular, elliptical or whatever. This is exactly what we have along the path of the inclined composite orbit in the above animation. Thus, in Situation 'B' [a fly-wheel precessing around a pivot stand] with the fly-wheel spinning at constant angular velocity ω and precessing at constant angular velocity Ω, the material of the fly-wheel is in a continuous state of acceleration.
Thus, the creation of an acceleration by two simultaneous rotations at constant angular velocity in mutually perpendicular planes is merely a matter of geometry. The physical phenomenon is exactly the same as that stated by Newton's Law: a linear force, externally applied to a material object, causes that object to accelerate while returning an equal and opposite inertial reaction.
I still need to answer the doubt that I left open as to whether or not Situation 'B' is dissipative as are the other 3 situations. Situation 'B' clearly involves the acceleration of the fly-wheel's material in opposition to an inertial reaction. So, as far as I can see, it must be consuming energy — or, rather, transducing it into inertial radiation. However, it doesn't appear to be much.
Perhaps Situation 'B' creates weak inertial radiation powered by the spin of the fly-wheel gradually slowing down. This small amount of power [if indeed it exists] could be measured as follows. Integrate an electric motor into the fly-wheel to maintain its angular velocity ω while it is precessing. Measure its electrical consumption over a long period. Then, for the same period, run the fly-wheel while it is not precessing to measure how much the motor consumed merely to overcome the friction in the bearings at the ends of the fly-wheels half-shafts. Subtract the two consumptions to see how much electrical energy was transmuted into inertial radiation.
It is now expedient to look again at Situation 'D' as depicted in the very large illustration [before the previous animation], which is displayed again in a smaller format below. The spinning fly-wheel is being forcibly rotated around the z-axis while being inhibited from precessing around the y-axis.
 While viewing the illustration on the right, it is possible to follow, in one's mind's eye, how a sink-hole on the rim of the spinning fly-wheel will move when the fly-wheel is forcibly rotated about the z-axis by the torque τ. Consider the simplest case where Ω = ω. When the sink-hole passes the point x = 0, y = 0, z = −R, it will have a path-speed of R × ω metres per second. However, when that same sink-hole passes the point x = R, y = 0, z = +R, its path-speed is the vector sum of R × ω and R × Ω. In this simplest case, this works out as the vector sum of R × ω and R × ω, that is √2 × R × ω.
While viewing the illustration on the right, it is possible to follow, in one's mind's eye, how a sink-hole on the rim of the spinning fly-wheel will move when the fly-wheel is forcibly rotated about the z-axis by the torque τ. Consider the simplest case where Ω = ω. When the sink-hole passes the point x = 0, y = 0, z = −R, it will have a path-speed of R × ω metres per second. However, when that same sink-hole passes the point x = R, y = 0, z = +R, its path-speed is the vector sum of R × ω and R × Ω. In this simplest case, this works out as the vector sum of R × ω and R × ω, that is √2 × R × ω.
Thus, as the sink-hole passes the second point mentioned above, its path speed is √2 times the path-speed it had when it passed the first point. Consequently, along the path it took from the first point to the second point, it underwent a forced acceleration. The orbit of the sink-hole, as it passes through all 4 quadrants, forms a kind of sine wave, bent in a sense that is perpendicular to its plane, inscribed around the surface of the sphere of radius R that contains the fly-wheel in all its positions as it is precessed around the z-axis.
So far, for ease of explanation, I set ω = Ω, which, in practical terms, means the fly-wheel is spinning quite slowly. If I spin up the fly-wheel so that ω >> Ω, the orbital track of each sink-hole will repeat many times as the fly-wheel is forcibly precessed, thereby causing each sink-hole to undergo more acceleration. The form of motion is nonetheless essentially the same: it's just that the track of any sink-hole on the surface of the fly-wheel's containing sphere, instead of looking like a simple sine wave, will look more like a curvily-wound ball of wool. And, of course, the torque τ needed to overcome the generated inertial reaction will have to be correspondingly greater.
The reason for the seemingly much greater inertial coupling to free space exhibited in Situation 'D' compared with Situation 'B' is because in Situation 'D', the torque τ is moving its point of application and is therefore doing work [dissipating energy] whereas in Situation 'B' the acceleration of the fly-wheel's 'mass' is simply countering a static force that is much smaller than its equivalent dead-weight.
Inertial Radiation
The above section establishes that the mechanism that generates inertial reaction to forced circular motion [of gyros and fly-wheels] is, in principle, exactly the same as for the forced linear motion stated in Newton's Law. It's simply that the dynamic geometry is a lot more complicated and is thereby superficially counter-intuitive.
Notwithstanding, it is evident that the dynamical geometry of such rotational mechanisms generates inertial reactions which are far more pronounced than in the case of the simple forced linear acceleration described by Newton's Law. Hence, rotational mechanisms should be much more effective generators of inertial radiation than objects being accelerated in straight lines.
I cannot imagine that it would be practical from an engineering point of view to fabricate fly-wheel mechanisms that could operate with fly-wheels spinning and being forcibly precessed at more than about 2500 rpm i.e. with ω = Ω ≅ 40 Hz. That is a very low frequency almost at the bottom of the humanly audible range. To produce any effect that would be experimentally detectable would probably require either a much higher frequency or impossibly enormous detection apparatus. Also, it would be necessary to investigate how such inertial radiation would be polarised and if it could be directed or focused.
The following is pure speculation on my part. Perhaps the narrow jets that seem to project matter and highly collimated radiation vast distances into interstellar space from the axial cusps of a toroidal rotating black hole or from the poles of a magnetar are driven by the inertial radiation produced by the phenomenon that I have described above.
Instead of rotating the heavy material of a physical fly-wheel, we could use electrons. Electrons are 'objects' that have 'mass'. So they could be revolved as a large electrical current within the metallic lattice of a heavy gauge circular copper pipe. The revolving electrons would thereby form a spinning fly-wheel whose outer rim was travelling at near light-speed. The copper pipe could then be forcibly precessed mechanically around a diameter [the z-axis], thereby creating a super-fast version of Situation 'D'. We could take this idea a step further by creating a magnetic containment field with the shape of the circular copper pipe. This could then be precessed by a system of coils powered with a rotating phase. The mechanism would then have no need of physical moving parts and so could be made to run even faster.
With such a device as this, it would be possible, I think, to conduct far more fruitful experiments.
Loss of Weight & Inertia
After all the above, I still feel that I am no closer to a conceptual understanding of what links the four observable and measurable physical quantities of force, 'mass', acceleration and inertial reaction.
A spinning precessing fly-wheel is undeniably observed to lose the greater portion of the inertia it has when not spinning and precessing. It seems that spinning and precessing somehow progressively isolate the fly-wheel from the universe: that is, it progressively reduces the fly-wheel's coupling with space-time.
The only tangible property I can see that may be causing this disconnection or de-coupling with the rest of the universe is the rapid cyclic acceleration and deceleration of all the matter of which the fly-wheel is composed. It is as if this rapid cyclic acceleration and deceleration generates inertial radiation, which creates some kind of 'near field' or 'æthereal cage' around the flywheel, which diverts gravitational influence — or even the flow of time itself.
On the other hand, perhaps what I said in the previous paragraph is a rather negative way of viewing the phenomenon. Perhaps it is the absence of force and acceleration that allows the universe to self-connect. Perhaps force is the moderator of the universe as are the graphite rods in a nuclear reactor: it progressively de-couples from each other the objects that make up the universe.
All this leaves me with the sense that Я [in my extended rendering of Newton's Law f = Я × m × a] is always there and that it is only truly equal to unity when the force f is zero. However, in the case of the magnitudes of force, mass and acceleration, within the bounds of human experience, it is so close to unity that its deviation from unity is fundamentally imperceptible.
There's an electrical counterpart for this. Electricity [not necessarily the individual electrons] travels along a power transmission line at about 270,000 km per second. At the 50 hertz power frequency, a ¼-wave dipole would span 1350 kilometres. And that's how far a virtual electron would travel back and forth within the power line. I don't think any country's national power grid would have a single span of power line that long. Yet, despite its length and the enormous power being transmitted, practically no electromagnetic radiation is generated. On the other hand, a radio transmitter, operating at 14½ MHz, moves virtual electrons back and forth over a distance of only 5 metres. Yet it create sufficient radiation to span the entire world with only 100 watts or so of power. In other words, for efficient radiation — coupling to free space — frequency is key.
So, by analogy, perhaps the reason we can perceive the loss-of-inertia phenomenon only with a gyroscopic device and not with a linearly accelerated object is because of the vastly higher frequency [rate of switching back and forth] of acceleration and deceleration of 'mass' in the case of the precessing fly-wheel. Perhaps, furthermore, the geometry and operation of Situation 'D' provides the best inertial match to the characteristics of space-time [what I have re-conceived as the æthereal time-flux] in the same way that a dipole antenna radiates with maximum efficiency when it matches exactly the impedance of free space Z0 = √(μ0÷ε0), which is 377 ohms.
μ0
is the magnetic permeability of free space.
ε0
is the electrical permittivity of free space.
An Inertial Transformer
An electrical transformer comprises a primary coil of conducting material such as copper plus a secondary coil, again of conducting material such as copper. The purpose of a transformer is to convert a small alternating electrical current supplied at a high alternating voltage fed to the primary coil into a high alternating current at a low alternating voltage in the secondary coil. Or vice versa.
When the coils are axially aligned, the degree of coupling, and hence the efficiency of energy transfer is maximised. When the axes of the two coils are perpendicular to each other, the degree of coupling, and hence the efficiency of energy transfer is minimised.
The degree of coupling between the two coils can be increased by including a magnetic core, of soft iron or ferrite, inside the coils along their combined axes. This effectively increases the reactance Z of the coils to a magnitude much higher than Z0, the reactance of free space. It is expedient to do this because the natural reactance of a coil, due to its physical geometry, is inevitably much higher than Z0. It is this that makes a transformer with a magnetic core so much more efficient.
Because the reactance Z of a transformer coil is so much higher than the reactance Z0 of free space, a transformer coil is inherently a bad radiator of 'electromagnetic' waves. A radio dipole, on the other hand has an out-bound impedance matched the that of free space. Consequently, a dipole is a very efficient radiator of 'electromagnetic' waves. So, although two parallel dipoles could, through their near field effect, act as a transformer, the energy transfer efficiency would not be too good because a lot would tend to radiate into space. It would be rather a leaky transformer.
This makes me curious as to whether it would be possible to get a clutch-type inertial near field coupling between two spinning precessing fly-wheels and thereby create an inertial transformer. Such an inertial clutch might be quite useful. Going one stage further, could a sustained spinning fly-wheel or electron stream, that is being forcibly precessed, be made to induce inertial loss into material that isn't spinning and precessing? If so, flying saucers suddenly begin to look far more practical.
Even now, a vast amount of experimenting still needs to be conducted to uncover the mysteries of the gyroscopic phenomenon. I think we may well find — as I have already conjectured — that there is ultimately only one kind of fundamental radiation and that so-called electromagnetic radiation is really inertial radiation seen from another direction of observation.
Practical Use
Force and inertial reaction are non-reversible. So are torque and its inertial reaction. Consequently, no resultant external directed force can be created from a torque or force-couple applied to the gyroscopic device. The energy expended [work done] by a directed externally applied force or torque must therefore become distributed [or dispersed]: entropy must increase.
The only product of applying a torque or force-couple to a gyroscopic device, which could possibly be used in an engineering application, is therefore the resulting inertial radiation. But for this, it would have to be possible for the inertial radiation to be directed and focused. Perhaps an inertial standing wave could be set up between a levitated vehicle and the ground. But that is wild speculation on my part.
At present the only use I can see for gyroscopic devices — which is indeed a very good one — is to provide a stable reference platform for navigation. And this is already well established.
Conclusion
In this essay, I have tried to show, however tenuously, that the basic concept of a universal æther, flowing into sink holes, can underpin the phenomena observed in revolutionary and rotational motion.
The conceptual model I have built, throughout this series of essays, is neither rigorous nor complete. But it is — for the most part — internally consistent.
My conceptual model is in no way consistent with the mainstream views of reality. But then the Standard Model of Physics and the Theory of Relativity are not consistent with each other.
My objective, in this series of essays, has not been to construct a new all singing and dancing alternative theory of everything to compete with the mainstream. My interest is not primarily in Physics. It is in the nature of human perception. It is in the various constructs or frameworks, which the human mind uses, to try to understand the universe to which its physical senses provide it with a raw view.
Many people think that, what they see as the laws of physics as expressed in mathematical formulas, are inherent to the universe. I do not agree. I think that all the laws, observed by man, are constructs that are entirely within the mind of man. They are simply frameworks, or systems of categorization, which the mind of man constructs around his observations, as a means of trying to get a handle on what he sees. The æthereal flow model, which I have constructed through this series of essays, is such a framework. And it works for me.
I have, on this web site, written essays about other personal views of the universe, which do not attempt to be consistent with the view expounded in this series of essays, or even with each other. But this mutual inconsistency is not a problem for me. This is because I know that none of my views are the universe. They are just means by which I can get some feel for the conscious experience I am still having of a vast environment in which I arrived almost 83 years ago. And that's OK.
It makes me realise that chasing an evermore elusive view, of ever-finer detail, of the physical universe is not what life is about. It is about constantly improving the way I, as a conscious entity, relate with other human beings.
© Aug 2016 to Jan 2017, 28 Nov to 18 Dec 2024 Robert John Morton |
PREV

 Considered in isolation, a sink-hole is a conceptual hole in space into which the universal æther continually flows from all directions equally in 3-dimensional space. A sink-hole is not dynamically affected by its own incoming flow of æther. This is because, from its own point of view, its own incoming flow is always symmetrical. It can only be perturbed by an asymmetry in the flow of æther in its vicinity. In other words, it can only be physically accelerated by a net flow of æther which is flowing through it, across it or past it but not into it.
Considered in isolation, a sink-hole is a conceptual hole in space into which the universal æther continually flows from all directions equally in 3-dimensional space. A sink-hole is not dynamically affected by its own incoming flow of æther. This is because, from its own point of view, its own incoming flow is always symmetrical. It can only be perturbed by an asymmetry in the flow of æther in its vicinity. In other words, it can only be physically accelerated by a net flow of æther which is flowing through it, across it or past it but not into it.
 However, if all the æther in the universe is flowing into sink holes, where does the æther, which flows through, across or past them, come from? The answer is, of course, the æther flowing into other sink holes. Across any point P in space, æther is flowing, in every direction, into what is ostensibly a homogeneous distribution of sink-holes S1, S2, S3 and so on, which populates the whole of space. Consequently, far from the immediate influence of any local sink-hole, the flow of the æther across any point P in space is spherically symmetrical both to and from any direction.
However, if all the æther in the universe is flowing into sink holes, where does the æther, which flows through, across or past them, come from? The answer is, of course, the æther flowing into other sink holes. Across any point P in space, æther is flowing, in every direction, into what is ostensibly a homogeneous distribution of sink-holes S1, S2, S3 and so on, which populates the whole of space. Consequently, far from the immediate influence of any local sink-hole, the flow of the æther across any point P in space is spherically symmetrical both to and from any direction.
 The mechanism of mutual attraction between two sink holes, in an otherwise empty universe, is illustrated on the right. However, only the mechanism whereby S1 attracts S2 is actually shown. Equally, S2 attracts S1, thus making the attraction mutual. The
The mechanism of mutual attraction between two sink holes, in an otherwise empty universe, is illustrated on the right. However, only the mechanism whereby S1 attracts S2 is actually shown. Equally, S2 attracts S1, thus making the attraction mutual. The  Suppose it's possible to hold sink holes S1 and S2 in place so that they can't move. To do this, it is necessary to apply a real directed force F, to each sink hole, in the direction away from its attractor. Let's imagine that the forces are applied by the Fingers of God. The sink holes experience real directed forces. But they are not accelerating through space. Each is in exactly the same situation as a person standing on the Earth experiencing the upward force of the ground on the bottoms of his feet.
Suppose it's possible to hold sink holes S1 and S2 in place so that they can't move. To do this, it is necessary to apply a real directed force F, to each sink hole, in the direction away from its attractor. Let's imagine that the forces are applied by the Fingers of God. The sink holes experience real directed forces. But they are not accelerating through space. Each is in exactly the same situation as a person standing on the Earth experiencing the upward force of the ground on the bottoms of his feet.
 Consider one of the sink-holes in isolation. The Finger of God exerts an external force F upon the sink-hole. This causes the sink hole to accelerate at a metres per second per second in the direction of the force. The sink hole is thus no longer "going with the flow" of its surrounding æther. This causes the flux density of the æther, flowing in the vicinity of the sink hole, to become spherically asymmetrical. This is depicted by the grey egg-shaped contour of constant flux density ρ in the diagram.
Consider one of the sink-holes in isolation. The Finger of God exerts an external force F upon the sink-hole. This causes the sink hole to accelerate at a metres per second per second in the direction of the force. The sink hole is thus no longer "going with the flow" of its surrounding æther. This causes the flux density of the æther, flowing in the vicinity of the sink hole, to become spherically asymmetrical. This is depicted by the grey egg-shaped contour of constant flux density ρ in the diagram.
 The principle of constrained revolution, is shown on the left in terms of a hollow rotating cylinder in free space. To create the sensation of Earth's gravity, it is necessary to make rω² = g, in which r is the radius of the cylinder, ω is the angular velocity with which the cylinder is rotating and g is the so-called acceleration of gravity at the Earth's surface, which is 9·80665 metres per second per second. A cylinder with a radius of 100 metres would therefore have to rotate at an angular velocity ω = √(g÷r) = √(9·80665÷100) = 0·313155712 radians per second to produce an "artificial gravity" of equal strength to that at the Earth's surface. This means that the cylinder would have to rotate once approximately every 20 seconds.
The principle of constrained revolution, is shown on the left in terms of a hollow rotating cylinder in free space. To create the sensation of Earth's gravity, it is necessary to make rω² = g, in which r is the radius of the cylinder, ω is the angular velocity with which the cylinder is rotating and g is the so-called acceleration of gravity at the Earth's surface, which is 9·80665 metres per second per second. A cylinder with a radius of 100 metres would therefore have to rotate at an angular velocity ω = √(g÷r) = √(9·80665÷100) = 0·313155712 radians per second to produce an "artificial gravity" of equal strength to that at the Earth's surface. This means that the cylinder would have to rotate once approximately every 20 seconds.
 A large rotating cylinder with people walking, sitting, eating, working and resting inside its torus-shaped rim is systemically complicated. I must abstract the essence of this phenomenon of "rotational gravity" and encapsulate it in a simpler form. For this purpose, I shall replace the rotating cylinder with a rotating dumbbell, as illustrated on the right, comprising two weights, joined together by a rigid weightless bar.
A large rotating cylinder with people walking, sitting, eating, working and resting inside its torus-shaped rim is systemically complicated. I must abstract the essence of this phenomenon of "rotational gravity" and encapsulate it in a simpler form. For this purpose, I shall replace the rotating cylinder with a rotating dumbbell, as illustrated on the right, comprising two weights, joined together by a rigid weightless bar.
 The weights mentioned above are merely vast agglomerations of sink holes. I may therefore replace each weight by a single sink hole. In doing so, however, I must also replace the centripetal force, exerted by the weightless bar, with a pair of inward opposing forces F exerted by the Fingers of God. The two sink holes are thus now in constrained revolution around the common centre. In this case, each of the revolving weights comprises just one sink hole: i.e. n = 1.
The weights mentioned above are merely vast agglomerations of sink holes. I may therefore replace each weight by a single sink hole. In doing so, however, I must also replace the centripetal force, exerted by the weightless bar, with a pair of inward opposing forces F exerted by the Fingers of God. The two sink holes are thus now in constrained revolution around the common centre. In this case, each of the revolving weights comprises just one sink hole: i.e. n = 1.
 Whenever external forces F are applied to two sink-holes, to keep them revolving around each other, the otherwise spherically symmetrical æthereal flux passing by each sink-hole becomes asymmetrical. This creates an up-stream density bow wave as depicted by the egg-shaped grey contour in the diagram on the right. However, each force F and its inertial reaction I now act in the opposite sense from what they did in the case of mutual attraction. The direction of decreasing æthereal density is also reversed, as is that of the æthereal bow-wave.
Whenever external forces F are applied to two sink-holes, to keep them revolving around each other, the otherwise spherically symmetrical æthereal flux passing by each sink-hole becomes asymmetrical. This creates an up-stream density bow wave as depicted by the egg-shaped grey contour in the diagram on the right. However, each force F and its inertial reaction I now act in the opposite sense from what they did in the case of mutual attraction. The direction of decreasing æthereal density is also reversed, as is that of the æthereal bow-wave.
 The whole situation is clarified by the combined diagram on the right. The sink hole is shown in the dead centre of an ellipsoidal envelope of constant æthereal flux density ρ. This means that the centrifugal inertial reaction plus the so-called gravitational inertial reaction add up to zero. The æthereal flux, passing by the sink-hole, is thus rarer along the major axis of the ellipsoid — in both directions — than it is in any other direction relative to the sink hole.
The whole situation is clarified by the combined diagram on the right. The sink hole is shown in the dead centre of an ellipsoidal envelope of constant æthereal flux density ρ. This means that the centrifugal inertial reaction plus the so-called gravitational inertial reaction add up to zero. The æthereal flux, passing by the sink-hole, is thus rarer along the major axis of the ellipsoid — in both directions — than it is in any other direction relative to the sink hole.
 Successive contours of constant æthereal flux density, which surround a sink hole alone in free space, are spherical, as shown on the left. On the other hand, the successive contours of constant æthereal flux density, which surround a sink hole in orbit, are not spherical.
Successive contours of constant æthereal flux density, which surround a sink hole alone in free space, are spherical, as shown on the left. On the other hand, the successive contours of constant æthereal flux density, which surround a sink hole in orbit, are not spherical.
 Successive contours of constant æthereal flux density, which surround a sink hole in free orbit with another, around their common centre of revolution, have the form of prolate ellipsoids. The major axes of these ellipsoids lie along the radial of revolution of the sink hole which they surround. Each sink hole lies at the centre of its concentric contours of constant flux density. The illustration on the right shows the situation for just one of the orbiting sink holes.
Successive contours of constant æthereal flux density, which surround a sink hole in free orbit with another, around their common centre of revolution, have the form of prolate ellipsoids. The major axes of these ellipsoids lie along the radial of revolution of the sink hole which they surround. Each sink hole lies at the centre of its concentric contours of constant flux density. The illustration on the right shows the situation for just one of the orbiting sink holes.
 Consider two identical planets freely orbiting each other around a common centre, as shown in the animation on the left. According to the æthereal hypothesis, which I have been building throughout this series of essays, these two planets are in blissful equilibrium, But they are not in equilibrium between two equal opposing real directed forces.
Consider two identical planets freely orbiting each other around a common centre, as shown in the animation on the left. According to the æthereal hypothesis, which I have been building throughout this series of essays, these two planets are in blissful equilibrium, But they are not in equilibrium between two equal opposing real directed forces.
 Consider an object like the green sphere on the right. It is perfectly at rest in free space. In other words, it is not accelerating. It is not in orbit around any other object. It is not rotating. It has a radius of R metres. According to my postulation, the substance of the sphere, at its most fundamental level, is composed of sink-holes. I shall take the liberty of assuming that these are homogeneously distributed, at least down to a small molecular level of granularity. I shall therefore consider the sphere to have a homogeneous density of ρ sink-holes per cubic metre.
Consider an object like the green sphere on the right. It is perfectly at rest in free space. In other words, it is not accelerating. It is not in orbit around any other object. It is not rotating. It has a radius of R metres. According to my postulation, the substance of the sphere, at its most fundamental level, is composed of sink-holes. I shall take the liberty of assuming that these are homogeneously distributed, at least down to a small molecular level of granularity. I shall therefore consider the sphere to have a homogeneous density of ρ sink-holes per cubic metre.
 Suppose now that the green sphere is rotating, as shown on the left, around an axis passing through its centre (black line), at an angular velocity of ω radians per second. I have postulated that all material objects are made up of æthereal sink-holes. Almost all the sink-holes, of which the green sphere is composed, will effectively be revolving around the sphere's axis of rotation at angular velocity ω. However, they will, for the most part, be revolving at different distances from the sphere's axis of rotation. Any sink-hole within the sphere, which is at a given orbital distance r from the axis of rotation, will suffer an inertial acceleration of rω², which acts radially outwards from the axis of rotation.
Suppose now that the green sphere is rotating, as shown on the left, around an axis passing through its centre (black line), at an angular velocity of ω radians per second. I have postulated that all material objects are made up of æthereal sink-holes. Almost all the sink-holes, of which the green sphere is composed, will effectively be revolving around the sphere's axis of rotation at angular velocity ω. However, they will, for the most part, be revolving at different distances from the sphere's axis of rotation. Any sink-hole within the sphere, which is at a given orbital distance r from the axis of rotation, will suffer an inertial acceleration of rω², which acts radially outwards from the axis of rotation.
 Consider the special case illustrated on the right of a sink-hole S, on the surface of the sphere, at the edge of the widest possible infinitely thin disc of radius R, whose plane is perpendicular to the sphere's axis of rotation. The sink-hole's spherically convergent inertial acceleration a = خRρ acts inwardly towards the centre of the sphere, while the sink-hole's cylindrically divergent inertial acceleration, Rω², caused by the sphere's rotation, acts outwardly away from the sphere's axis of rotation. Consequently, there must exist an angular velocity ωf at which Rωf² becomes equal and opposite to خRρ, leaving the sink-hole itself in the weightless state of free orbit.
Consider the special case illustrated on the right of a sink-hole S, on the surface of the sphere, at the edge of the widest possible infinitely thin disc of radius R, whose plane is perpendicular to the sphere's axis of rotation. The sink-hole's spherically convergent inertial acceleration a = خRρ acts inwardly towards the centre of the sphere, while the sink-hole's cylindrically divergent inertial acceleration, Rω², caused by the sphere's rotation, acts outwardly away from the sphere's axis of rotation. Consequently, there must exist an angular velocity ωf at which Rωf² becomes equal and opposite to خRρ, leaving the sink-hole itself in the weightless state of free orbit.
 The resulting deformation in shape of the sink hole's otherwise spherical contours of constant æthereal flux density is shown on the left. They have become ellipsoidal. The sink hole is at the centre of the ellipsoids. This means that the centrifugal acceleration rωf² plus the so-called gravitational acceleration rخρ add up to zero. The æthereal flux passing the sink hole is thus denser along the major axis of the ellipsoids than it is in any other direction.
The resulting deformation in shape of the sink hole's otherwise spherical contours of constant æthereal flux density is shown on the left. They have become ellipsoidal. The sink hole is at the centre of the ellipsoids. This means that the centrifugal acceleration rωf² plus the so-called gravitational acceleration rخρ add up to zero. The æthereal flux passing the sink hole is thus denser along the major axis of the ellipsoids than it is in any other direction.
 Now consider a sink-hole S, as shown on the right, within that same thin disc but not on its outer surface. This sink-hole is located at a radial distance r (less than R) from the sphere's axis of rotation. The spherically-symmetrical inward inertial acceleration a, acting upon this sink-hole, is خ × ρ × r. This is exactly the same as for a smaller sphere of total radius r. This is because, within the sub-sphere (stronger blue) of radius r, the influence of all the sink-holes that lie outside it — i.e. between the radius r and the radius R (lighter blue) — cancels to zero.
Now consider a sink-hole S, as shown on the right, within that same thin disc but not on its outer surface. This sink-hole is located at a radial distance r (less than R) from the sphere's axis of rotation. The spherically-symmetrical inward inertial acceleration a, acting upon this sink-hole, is خ × ρ × r. This is exactly the same as for a smaller sphere of total radius r. This is because, within the sub-sphere (stronger blue) of radius r, the influence of all the sink-holes that lie outside it — i.e. between the radius r and the radius R (lighter blue) — cancels to zero.
 What about the sink-holes of the sphere that are outside this central thin disc? Consider a sink-hole S located on the sphere's surface at the edge of a smaller thin disc which is off-set along the axis of rotation at "latitude" θ from the sphere's "equator". This situation is shown on the left. CL is a circle of longitude, which passes twice through the axis of rotation — once at each "pole". The smaller thin disc (green) has a radius of Rcosθ and is off-set from the centre of the sphere along its axis of rotation by a distance of Rsinθ. As always, the sink-hole S suffers a spherically-symmetrical inward inertial acceleration of خρ, along the radial R, towards the centre of the sphere.
What about the sink-holes of the sphere that are outside this central thin disc? Consider a sink-hole S located on the sphere's surface at the edge of a smaller thin disc which is off-set along the axis of rotation at "latitude" θ from the sphere's "equator". This situation is shown on the left. CL is a circle of longitude, which passes twice through the axis of rotation — once at each "pole". The smaller thin disc (green) has a radius of Rcosθ and is off-set from the centre of the sphere along its axis of rotation by a distance of Rsinθ. As always, the sink-hole S suffers a spherically-symmetrical inward inertial acceleration of خρ, along the radial R, towards the centre of the sphere.
 Thus, any spinning object has both an inward æthereal flux asymmetry (bow wave) and an outward æthereal flux asymmetry (bow wave). These are depicted, as best as I am able to represent them, in the illustration on the right. The spinning object is spherical. This causes the profile of its æthereal flux asymmetry to have the form of an ellipsoidal disc. I have taken artistic license by showing the radius of the disc-shaped outward contour of constant flux density as being greater than that of the spherical inward contour of constant flux density. However, this is purely to help to make them separately visible.
Thus, any spinning object has both an inward æthereal flux asymmetry (bow wave) and an outward æthereal flux asymmetry (bow wave). These are depicted, as best as I am able to represent them, in the illustration on the right. The spinning object is spherical. This causes the profile of its æthereal flux asymmetry to have the form of an ellipsoidal disc. I have taken artistic license by showing the radius of the disc-shaped outward contour of constant flux density as being greater than that of the spherical inward contour of constant flux density. However, this is purely to help to make them separately visible.
 The special case, described above, of the central thin disc of a rotating sphere, is of particular interest. This is because, within this thin disc, it is possible for the two opposing æthereal density gradients to be equal and therefore cancel each other out. I would therefore like to explore this special case further. To do this, I shall remove the whole of the material of the sphere, except for this central thin spinning disc. The result is, in principle, the fly-wheel, as illustrated on the left, of radius R, rotating with angular velocity of ω radians per second around an axis which passes through its centre perpendicularly to the plane of the disc. The letter S signifies an arbitrary sink hole, located on the surface of the fly-wheel and which is itself part of the material of the fly-wheel.
The special case, described above, of the central thin disc of a rotating sphere, is of particular interest. This is because, within this thin disc, it is possible for the two opposing æthereal density gradients to be equal and therefore cancel each other out. I would therefore like to explore this special case further. To do this, I shall remove the whole of the material of the sphere, except for this central thin spinning disc. The result is, in principle, the fly-wheel, as illustrated on the left, of radius R, rotating with angular velocity of ω radians per second around an axis which passes through its centre perpendicularly to the plane of the disc. The letter S signifies an arbitrary sink hole, located on the surface of the fly-wheel and which is itself part of the material of the fly-wheel.

 The implication was that, unlike the pendulum that we had been studying previously, the gyro's frame of reference was not the Earth. Its orientation was not determined — or even influenced — by Earth's gravity. Instead, it seemed to strive to keep its axis aligned with an absolute direction in free space. So its frame of reference was not the Earth, the Sun or even the solar system. It was the Universe itself. It seems that a rapidly rotating mass has a mysterious directional coupling with space itself. And this coupling is quite strong. A gyro's insistence to keep its direction fixed with respect to the Universe, is evinced by two problems encountered when using the properties of the gyro to help with terrestrial navigation.
The implication was that, unlike the pendulum that we had been studying previously, the gyro's frame of reference was not the Earth. Its orientation was not determined — or even influenced — by Earth's gravity. Instead, it seemed to strive to keep its axis aligned with an absolute direction in free space. So its frame of reference was not the Earth, the Sun or even the solar system. It was the Universe itself. It seems that a rapidly rotating mass has a mysterious directional coupling with space itself. And this coupling is quite strong. A gyro's insistence to keep its direction fixed with respect to the Universe, is evinced by two problems encountered when using the properties of the gyro to help with terrestrial navigation.

 The diagram on the right shows what happens if the force-couple is allowed to act on the ends of the fly-wheel's shaft [assuming the fly-wheel isn't spinning] to rotate the fly-wheel by 20° around a line through its diameter.
The diagram on the right shows what happens if the force-couple is allowed to act on the ends of the fly-wheel's shaft [assuming the fly-wheel isn't spinning] to rotate the fly-wheel by 20° around a line through its diameter.
 Let's apply a torque τ to the ends of the shaft as shown by the mauve coloured arrows. The torque τ is acting within a vertical plane which is perpendicular to the plane of the disc. The torque is attempting to rotate the disc around its horizontal diameter. This causes the disc to undergo an angular acceleration Ω' [dΩ/dt] around its horizontal diameter. This angular acceleration will continue as long as the torque τ continues to be applied. If and when τ is removed, the disc will continue rotating at the angular velocity it attained during the time that the torque was applied. To slow the rotation of the disc back down to zero again, the same torque τ must be applied in the opposite sense for the same amount of time.
Let's apply a torque τ to the ends of the shaft as shown by the mauve coloured arrows. The torque τ is acting within a vertical plane which is perpendicular to the plane of the disc. The torque is attempting to rotate the disc around its horizontal diameter. This causes the disc to undergo an angular acceleration Ω' [dΩ/dt] around its horizontal diameter. This angular acceleration will continue as long as the torque τ continues to be applied. If and when τ is removed, the disc will continue rotating at the angular velocity it attained during the time that the torque was applied. To slow the rotation of the disc back down to zero again, the same torque τ must be applied in the opposite sense for the same amount of time.
 But remember that a torque is more than simply a force-couple. It is what we may call a double force-moment: each half of this double force-moment comprises 1) an applied force and 2) a radial distance [at which the force acts] from the central axis-of-twist. The radial distance is ostensibly perpendicular to the direction of the force.
The two halves of a torque do not have to be symmetrical, although they usually are. One half of the torque can be a small force acting at a large radius, whereas the other can be a large force acting at a small radius. What must be symmetrical are the 2 half-moments of the torque; that is: force × radial distance must be the same for both halves.
But remember that a torque is more than simply a force-couple. It is what we may call a double force-moment: each half of this double force-moment comprises 1) an applied force and 2) a radial distance [at which the force acts] from the central axis-of-twist. The radial distance is ostensibly perpendicular to the direction of the force.
The two halves of a torque do not have to be symmetrical, although they usually are. One half of the torque can be a small force acting at a large radius, whereas the other can be a large force acting at a small radius. What must be symmetrical are the 2 half-moments of the torque; that is: force × radial distance must be the same for both halves.
 Now set the disc rotating around its shaft axis at angular velocity ω, as shown on the right. The modest 4·4 radians per second, of the previous animation, will suffice — just so long as this rate is maintained in the long term by some unspecified means. Now apply the torque τ as before. This time, the disc behaves differently. It does not rotate about the horizontal axis through its diameter as before. Instead, it rotates about its vertical diametric axis, as indicated by the circular blue arrow. Furthermore, it does not undergo an angular acceleration Ω'. Instead, it instantly acquires, and then continues to rotate at, a constant angular velocity Ω.
Now set the disc rotating around its shaft axis at angular velocity ω, as shown on the right. The modest 4·4 radians per second, of the previous animation, will suffice — just so long as this rate is maintained in the long term by some unspecified means. Now apply the torque τ as before. This time, the disc behaves differently. It does not rotate about the horizontal axis through its diameter as before. Instead, it rotates about its vertical diametric axis, as indicated by the circular blue arrow. Furthermore, it does not undergo an angular acceleration Ω'. Instead, it instantly acquires, and then continues to rotate at, a constant angular velocity Ω.


 Conventional physics asserts that the fly-wheel is still being subjected to a torque τ. One half of τ's force-couple is thought to be the upward force, which the cone-headed support exerts upon the anchored end of the shaft. The other half-couple is imagined as an equal and opposite downward force exerted at the other end of the shaft, but which is, in really, thought to be double this force exerted downwards at the centre of the shaft by the weight of the fly-wheel.
Conventional physics asserts that the fly-wheel is still being subjected to a torque τ. One half of τ's force-couple is thought to be the upward force, which the cone-headed support exerts upon the anchored end of the shaft. The other half-couple is imagined as an equal and opposite downward force exerted at the other end of the shaft, but which is, in really, thought to be double this force exerted downwards at the centre of the shaft by the weight of the fly-wheel.
 The thrust of the rocket exerts a force F, at the free end of the fly-wheel's shaft, perpendicular to the fly-wheel's axis of rotation, as shown on the right. This causes the fly-wheel to precess around the force's line of action. An equal and opposite inertial reaction I to the force F must exist. It does. However, the rotating precessing fly-wheel appears to have off-set this inertial reaction laterally from the line of action of the force.
The thrust of the rocket exerts a force F, at the free end of the fly-wheel's shaft, perpendicular to the fly-wheel's axis of rotation, as shown on the right. This causes the fly-wheel to precess around the force's line of action. An equal and opposite inertial reaction I to the force F must exist. It does. However, the rotating precessing fly-wheel appears to have off-set this inertial reaction laterally from the line of action of the force.


 In the adjacent diagram, the viewer is looking along the fly-wheel's axis of rotation, from beyond the fly-wheel's orbit of precession, towards the support stand at the centre of the orbit. The fly-wheel is rotating anti-clockwise at an angular velocity of ω radians per second. The fly-wheel's direction of precession around its orbit is from left to right at a tangential velocity of RΩ metres per second, where R is the radius of the orbit in metres. The sink hole's tangential velocity around the fly-wheel is rω metres per second, where r is the radius of the fly-wheel in metres. The component of the sink hole's tangential velocity rω in the direction of orbital precession is rω.sin(θ).
In the adjacent diagram, the viewer is looking along the fly-wheel's axis of rotation, from beyond the fly-wheel's orbit of precession, towards the support stand at the centre of the orbit. The fly-wheel is rotating anti-clockwise at an angular velocity of ω radians per second. The fly-wheel's direction of precession around its orbit is from left to right at a tangential velocity of RΩ metres per second, where R is the radius of the orbit in metres. The sink hole's tangential velocity around the fly-wheel is rω metres per second, where r is the radius of the fly-wheel in metres. The component of the sink hole's tangential velocity rω in the direction of orbital precession is rω.sin(θ).
 The sink hole is law-bound to exert an equal and opposite inertial reaction Is to the force Fs. As illustrated on the right, Is is much larger for a sink hole below the fly-wheel's axis of rotation than it is for a sink hole above it. The difference in Is for a sink hole below the fly-wheel's axis of rotation, and for a sink hole above it, forms an anti-clockwise torque around the fly-wheel's horizontal diameter, which the fly-wheel's shaft translates into a torque τs around the support point. Now let us consider the cumulative effect of all the sink holes that make up the material of the fly-wheel.
The sink hole is law-bound to exert an equal and opposite inertial reaction Is to the force Fs. As illustrated on the right, Is is much larger for a sink hole below the fly-wheel's axis of rotation than it is for a sink hole above it. The difference in Is for a sink hole below the fly-wheel's axis of rotation, and for a sink hole above it, forms an anti-clockwise torque around the fly-wheel's horizontal diameter, which the fly-wheel's shaft translates into a torque τs around the support point. Now let us consider the cumulative effect of all the sink holes that make up the material of the fly-wheel.
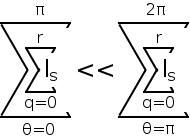 The inner sigma symbols, in the illustration on the left, are both the same. They sum the effects of all sink holes, within the material of the fly-wheel, which lie along an infinitely thin radial. That is, between q=0 and q=r, where q is a variable radius within the circle of the fly-wheel. The outer sigmas sum Is for all sink holes in the top half of the fly-wheel and all sink holes in the bottom half of the fly-wheel respectively.
The inner sigma symbols, in the illustration on the left, are both the same. They sum the effects of all sink holes, within the material of the fly-wheel, which lie along an infinitely thin radial. That is, between q=0 and q=r, where q is a variable radius within the circle of the fly-wheel. The outer sigmas sum Is for all sink holes in the top half of the fly-wheel and all sink holes in the bottom half of the fly-wheel respectively.
 A spinning fly-wheel can adopt a mode of precession in which its shaft is tilted upwards from the horizontal as shown on the left. Its orbit of precession, which is smaller than before, can be thought of as a circle of latitude ψ on an imaginary sphere whose equator (the grey circle) was the fly-wheel's orbit of precession when its shaft was horizontal. The plane of the orbit of the sink hole around the rim of the fly-wheel is now no longer parallel to the direction of the force exerted by the support stand.
A spinning fly-wheel can adopt a mode of precession in which its shaft is tilted upwards from the horizontal as shown on the left. Its orbit of precession, which is smaller than before, can be thought of as a circle of latitude ψ on an imaginary sphere whose equator (the grey circle) was the fly-wheel's orbit of precession when its shaft was horizontal. The plane of the orbit of the sink hole around the rim of the fly-wheel is now no longer parallel to the direction of the force exerted by the support stand.
 Now let us revert to considering the whole fly-wheel disc: not just a single sink hole on its outer rim. How can I cause a spinning fly-wheel to adopt this tilted mode of precession? Starting with the fly-wheel disc precessing with its shaft horizontal, how can I cause its shaft to lift so that it becomes tilted upwards at an angle ψ as shown on the right? I push the shaft round horizontally in the direction in which it is precessing. As I do so, the shaft tilts upwards by revolving around the support point in a direction perpendicular to that in which I push it.
Now let us revert to considering the whole fly-wheel disc: not just a single sink hole on its outer rim. How can I cause a spinning fly-wheel to adopt this tilted mode of precession? Starting with the fly-wheel disc precessing with its shaft horizontal, how can I cause its shaft to lift so that it becomes tilted upwards at an angle ψ as shown on the right? I push the shaft round horizontally in the direction in which it is precessing. As I do so, the shaft tilts upwards by revolving around the support point in a direction perpendicular to that in which I push it.
 The surprise is that the torque that needs to be exerted to elevate the fly-wheel is very small compared with the would-be dead weight W of the fly-wheel. The upward force Fψ exerted on the tilted shaft is greater than the upward force F0 was when the shaft were horizontal. Notwithstanding, it is still not equal to the dead weight W of the fly-wheel. I would guess that the ratio between W, Fψ and F0 somehow involves the cosine of the angle ψ. If I push the shaft in the direction of precession until it becomes vertical (ψ=½π), the upward force F½π on the support becomes the dead weight W of the fly-wheel.
The surprise is that the torque that needs to be exerted to elevate the fly-wheel is very small compared with the would-be dead weight W of the fly-wheel. The upward force Fψ exerted on the tilted shaft is greater than the upward force F0 was when the shaft were horizontal. Notwithstanding, it is still not equal to the dead weight W of the fly-wheel. I would guess that the ratio between W, Fψ and F0 somehow involves the cosine of the angle ψ. If I push the shaft in the direction of precession until it becomes vertical (ψ=½π), the upward force F½π on the support becomes the dead weight W of the fly-wheel.
 Imagine the fly-wheel back in free space. The support stand is a rocket. If the fly-wheel is not rotating or precessing, the force F required to accelerate it at a fixed rate a is given by the equation F=m×a, where m is the mass of the fly-wheel. If it is rotating and precessing, the equation must be qualified with the subscript ψ viz. Fψ=mψ×a because the mass mψ of the fly-wheel decreases as the angle ψ increases. Consequently, the force Fψ necessary to keep the fly-wheel accelerating at a constant rate of a must decrease as the angle ψ increases.
Imagine the fly-wheel back in free space. The support stand is a rocket. If the fly-wheel is not rotating or precessing, the force F required to accelerate it at a fixed rate a is given by the equation F=m×a, where m is the mass of the fly-wheel. If it is rotating and precessing, the equation must be qualified with the subscript ψ viz. Fψ=mψ×a because the mass mψ of the fly-wheel decreases as the angle ψ increases. Consequently, the force Fψ necessary to keep the fly-wheel accelerating at a constant rate of a must decrease as the angle ψ increases.




 In the animation, I made Ω = ω. Consequently, each time a sink hole passes the uppermost point, it isn't actually revolving around anything. It is completely stationary with respect to the support point. This leaves the radial in-flow of its æthereal flux spherically symmetrical. Thus, the æthereal flux density gradient, at any given radial distance from the sink hole, is the same in all directions.
In the animation, I made Ω = ω. Consequently, each time a sink hole passes the uppermost point, it isn't actually revolving around anything. It is completely stationary with respect to the support point. This leaves the radial in-flow of its æthereal flux spherically symmetrical. Thus, the æthereal flux density gradient, at any given radial distance from the sink hole, is the same in all directions.
 Conversely, each time a sink hole passes the lowest point, it is moving at its maximum angular velocity 2Ω around the axis of the fly-wheel. As a result of the centrifugal inertial reaction thus generated, the radial in-flow of its æthereal flux is at its most asymmetrical. Thus, the æthereal flux density gradient, at any given radial distance from the sink hole, is different in different directions. Specifically, in all but a small solid angle of directions, the æthereal flux density gradient is, in this case, very much higher.
Conversely, each time a sink hole passes the lowest point, it is moving at its maximum angular velocity 2Ω around the axis of the fly-wheel. As a result of the centrifugal inertial reaction thus generated, the radial in-flow of its æthereal flux is at its most asymmetrical. Thus, the æthereal flux density gradient, at any given radial distance from the sink hole, is different in different directions. Specifically, in all but a small solid angle of directions, the æthereal flux density gradient is, in this case, very much higher.
 Consequently, the inertial reaction I of the sink hole to any real directed force, applied in the upward direction, is significantly less. In effect, from the point of view of this force, my universal constant, which I have previously called k, is effectively multiplied by the asymmetry ratio α of the outward to inward radial flux density gradients. The ratio α is of course fractional.
Consequently, the inertial reaction I of the sink hole to any real directed force, applied in the upward direction, is significantly less. In effect, from the point of view of this force, my universal constant, which I have previously called k, is effectively multiplied by the asymmetry ratio α of the outward to inward radial flux density gradients. The ratio α is of course fractional.
 The proportional weight loss of the fly-wheel is the same as its "mass loss" ratio α in the upward vertical direction. So the relevant value of α is the ratio a:b where a and b are measured along the vertical radial of the fly-wheel as shown on the right. Of course, this only applies when the sink hole is at the bottom of the fly-wheel. The value of α for all the sink holes at all other places within the material of the fly-wheel must be greater.
The proportional weight loss of the fly-wheel is the same as its "mass loss" ratio α in the upward vertical direction. So the relevant value of α is the ratio a:b where a and b are measured along the vertical radial of the fly-wheel as shown on the right. Of course, this only applies when the sink hole is at the bottom of the fly-wheel. The value of α for all the sink holes at all other places within the material of the fly-wheel must be greater.
 As can be seen from the above diagram, when ω=Ω (when the prolate ellipsoidal contour of constant flux density lies at 45° to the vertical), the distances a and b are not very different. So α is a fairly large fraction. Consequently, the effective "mass-loss" of the fly-wheel is not very great. However, if we rev up the fly-wheel to make ω very much greater than Ω, the contour tilts much more towards the vertical, making α a much smaller fraction.
As can be seen from the above diagram, when ω=Ω (when the prolate ellipsoidal contour of constant flux density lies at 45° to the vertical), the distances a and b are not very different. So α is a fairly large fraction. Consequently, the effective "mass-loss" of the fly-wheel is not very great. However, if we rev up the fly-wheel to make ω very much greater than Ω, the contour tilts much more towards the vertical, making α a much smaller fraction.

