 Em uma noite tropical clara, fora no campo longe das luzes da cidade, adoro olhar para o céu. Eu vejo, em várias ocasiões, a Via Láctea, a Cruz do Sul e o Orion com Betelgeuse na esquina. Tudo parece majestoso, pacífico e imóvel. Mas na realidade, todas as estrelas estão em movimento constante em relação umas com as outras. Betelgeuse é tão grande que, se fosse onde o sol está, engoliria todos os planetas internos dentro de sua superfície contorcida. Mesmo o tamanho e a forma da nebulosa gigante à direita, conhecida como a Mão de Deus, está mudando constantemente. As galáxias todas rodam e traduzem-se umas com as outras, assim como fazem moléculas e átomos.
Em uma noite tropical clara, fora no campo longe das luzes da cidade, adoro olhar para o céu. Eu vejo, em várias ocasiões, a Via Láctea, a Cruz do Sul e o Orion com Betelgeuse na esquina. Tudo parece majestoso, pacífico e imóvel. Mas na realidade, todas as estrelas estão em movimento constante em relação umas com as outras. Betelgeuse é tão grande que, se fosse onde o sol está, engoliria todos os planetas internos dentro de sua superfície contorcida. Mesmo o tamanho e a forma da nebulosa gigante à direita, conhecida como a Mão de Deus, está mudando constantemente. As galáxias todas rodam e traduzem-se umas com as outras, assim como fazem moléculas e átomos.
Não obstante, o movimento, no contexto do universo, não é exatamente o mesmo que é percebido por seres humanos na vida cotidiana aqui na superfície da Terra. A percepção humana do movimento se desenvolveu dentro de um ambiente, que é fundamentalmente diferente de espaço universal. A biosfera terrestre é o único e abrangente quadro de referência para a experiência humana do movimento. Conseqüentemente, é a linha de base da estacionança, da qual a mente humana quantifica a sua noção de movimento. Porque, para nós, é tão abrangente, isso nos dá a sensação de que o movimento tem uma medida absoluta. Afinal, a maioria das coisas que vemos - como montanhas, lagos, árvores e edifícios - sempre ficam onde estão. Mesmo as coisas que se movem - como pessoas, vacas, bolas e carros - geralmente gastam mais tempo em repouso do que em movimento.
 Quando criança, eu familiarizei-me com muitos tipos diferentes de coisas que se movem, que eu encontrei principalmente na casa de meus avós e ao redor dela. No entanto, penso que a primeira coisa, que eu mentalmente abstrai como um objeto móvel independente, era uma bola suave com a qual eu jogava no jardim dos meus avós.
Quando criança, eu familiarizei-me com muitos tipos diferentes de coisas que se movem, que eu encontrei principalmente na casa de meus avós e ao redor dela. No entanto, penso que a primeira coisa, que eu mentalmente abstrai como um objeto móvel independente, era uma bola suave com a qual eu jogava no jardim dos meus avós.
A principal razão pela qual eu era capaz de abstrair mentalmente a minha bola como um objeto móvel independente era que eu podia ver claramente seu movimento relativo a mim e ao resto do mundo. Quando eu joguei a minha bola, percebi que seu movimento era muito complexo. Obviamente, não moveu-se em linha reta. No entanto, as minhas redes neurais pareciam capazes de racionalizar o movimento da bola, de modo a que se pareçou bastante normal para mim. Mesmo quando eu rolei minha bola no gramado, seu movimento ainda não era simples. Seu atrito com a grama causou-se desacelerar não linearmente. Mas esse movimento também foi racionalizado dentro da minha mente como outro tipo de movimento normal.
Muitos anos depois, quando comecei a estudar matemática e física na escola, a minha curiosidade foi desencadeada para analisar os aspectos mais fundamentais dos movimentos que observei com a minha bola de infância. Eu tinha atingido uma época em que a minha mente conseguiu criar situações abstratas nas quais o atrito do ar e grama - e até mesmo os efeitos da gravidade - foram removidos. Consegui perceber a noção de velocidade não contaminada.
De dentro de tais situações abstratas - ou experimentos de pensamento - eu poderia ver claramente que um objeto imperturbado permanece onde está, relativo a mim, ou muda sua posição em relação a mim a uma taxa constante. É estacionário em relação a mim ou está movendo-se com velocidade constante para mim ou para longe de mim. O aspecto relativo da velocidade persuade-me de que a condição estacionária é simplesmente um caso especial de velocidade relativa. É meramente uma velocidade relativa de zero.
Não foi há muito tempo atrás, que percebi, que, se o imolestado objeto, que estou observando, está movendo-se ao longo de um caminho, que não está diretamente alinhado comigo, não estará movendo-se a uma constante velocidade relativa a mim. Ele estará sempre - a uma maior ou a uma menor extensão - em um estado de aceleraçaõ ou desaceleração relativamente a mim. A grande significação disto é que a aceleração e a deceleração envolvidas não são provocadas por nenhuma dirigida força externa.
Aceleração Passiva
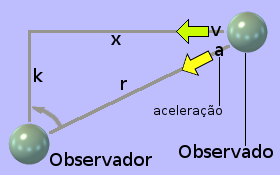 O diagrama à esquerda mostra um objeto que viaja através do espaço vazio ao longo do eixo dos x em uma velocidade v dentro do quadro de referência de um observador. O objeto passará mais próximo do observador a uma distância k. O observador vê o objeto vindo para ele como se fosse diretamente ao longo da pista hipotenusa r. Para o observador, o objeto parece estar se movendo em direção a ele a uma velocidade cada vez menor.
O diagrama à esquerda mostra um objeto que viaja através do espaço vazio ao longo do eixo dos x em uma velocidade v dentro do quadro de referência de um observador. O objeto passará mais próximo do observador a uma distância k. O observador vê o objeto vindo para ele como se fosse diretamente ao longo da pista hipotenusa r. Para o observador, o objeto parece estar se movendo em direção a ele a uma velocidade cada vez menor.
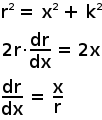 No triângulo mostrado acima, k é constante, enquanto x e r diminuem com o tempo. Como k é a distância de abordagem mais próxima, o triângulo tem ângulo de 90°. Os lados x, r e k são, portanto, relacionados pela regra dos quadrados de Pitágoras, como mostrado à direita. Como k é constante, a taxa em que r muda com x pode ser calculada por diferenciar a equação de Pitágoras como mostrado à direita.
No triângulo mostrado acima, k é constante, enquanto x e r diminuem com o tempo. Como k é a distância de abordagem mais próxima, o triângulo tem ângulo de 90°. Os lados x, r e k são, portanto, relacionados pela regra dos quadrados de Pitágoras, como mostrado à direita. Como k é constante, a taxa em que r muda com x pode ser calculada por diferenciar a equação de Pitágoras como mostrado à direita.
 Usar a regra de cadeia para diferenciação, agora podemos descobrir como a distância r varia ao longo do tempo. O diferencial de x em relação ao tempo é a velocidade v do objeto ao longo do eixo dos x. Isso nós consideramos constante porque decretamos que o objeto viaja ao longo de seu caminho a velocidade constante. Nenhuma força está agindo sobre isso.
Usar a regra de cadeia para diferenciação, agora podemos descobrir como a distância r varia ao longo do tempo. O diferencial de x em relação ao tempo é a velocidade v do objeto ao longo do eixo dos x. Isso nós consideramos constante porque decretamos que o objeto viaja ao longo de seu caminho a velocidade constante. Nenhuma força está agindo sobre isso.
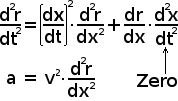 A tarefa agora é descobrir se, e se assim for, por quanto, o objeto está acelerando, ao longo do caminho r, em direção ao observador. Usando a regra padrão para calcular a segunda derivada, encontramos que o segundo termo é zero porque decretamos que a velocidade, v, do objeto ao longo do eixo x seja constante.
A tarefa agora é descobrir se, e se assim for, por quanto, o objeto está acelerando, ao longo do caminho r, em direção ao observador. Usando a regra padrão para calcular a segunda derivada, encontramos que o segundo termo é zero porque decretamos que a velocidade, v, do objeto ao longo do eixo x seja constante.
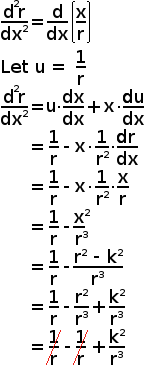 Para completar o cálculo da aceleração, a, ao longo de r, devemos avaliar a segunda derivada de r em relação a x. Esta é efetivamente a derivada da primeira derivada de r em relação a x, que descobrimos ser x / r. Em vez de lidar com o recíproco de r, prefiro substituir uma nova variável u = 1 / r. Então o problema se torna diferenciar o produto das duas variáveis relacionadas x e u.
Para completar o cálculo da aceleração, a, ao longo de r, devemos avaliar a segunda derivada de r em relação a x. Esta é efetivamente a derivada da primeira derivada de r em relação a x, que descobrimos ser x / r. Em vez de lidar com o recíproco de r, prefiro substituir uma nova variável u = 1 / r. Então o problema se torna diferenciar o produto das duas variáveis relacionadas x e u.
À esquerda, usei a regra do produto para encontrar a segunda derivada. Eu coloquei cada passo laborioso no processo, em vez de pular vários passos ao mesmo tempo, para que ninguém possa encontrar nenhum problema para segui-lo. A minha esperança é que eu realmente tenha conseguido certo, já que há muitas décadas desde que eu estava ativamente fazendo esse tipo de matemática. No resultado, k2/r3, k2 é uma constante. Portanto, a taxa de mudança da taxa de mudança de r em relação a x é inversamente proporcional a r3. Para obter a aceleração, a, ao longo da linha direta entre o observado e o observador, simplesmente precisamos multiplicar esse resultado pela v2.
 Uma vez que v2 é também uma constante, a aceleração, a, do objeto para o observador ao longo de r ainda é inversamente proporcional ao r3. Assim, é extremamente não-linear.
Uma vez que v2 é também uma constante, a aceleração, a, do objeto para o observador ao longo de r ainda é inversamente proporcional ao r3. Assim, é extremamente não-linear.
É claro que se diferenciar para encontrar a taxa de mudança de aceleração, a taxa de mudança da taxa de mudança de aceleração e assim por diante, envolverá potências inversas ainda maiores de r. Cada diferencial sucessivo terá o sinal oposto de seu antecessor e contribuirá cada vez menos com a natureza do movimento relativo entre o objeto e seu observador. A verdadeira forma final da aceleração de um objeto em relação ao seu observador será a amalgamação de uma série infinita de diferenciais.
Não obstante, o resultado claro é que cada um de dois corpos que viajam pelo espaço a diferentes velocidades constantes (sem força externa ou distorção gravitacional agindo sobre qualquer um) experimentará o outro desacelerando durante a sua abordagem e depois acelerando longe durante o seu retiro. É como se um atirador no chão jogasse uma bola para um coletor acima em uma árvore. A bola sobe em direção ao coletor e depois cai novamente antes que o coletor possa agarrá-lo. Note, no entanto, que a fórmula para a aceleração por gravidade é um pouco diferente.
Um bom senso desse tipo de movimento pode ser obtido pela observação de uma torre de água, celular ou microondas a alguma distância da pista, conforme você passa por ela em um trem de alta velocidade ou observando a torre de controle em um aeroporto a partir de uma aeronave como está pousando.
Assumimos que o cenário acima ocorre em um universo vazio sem estrelas para dar qualquer sentido de um quadro de referência mais universal. Os únicos objetos neste universo são o observador e o observado. Sem um fundo estrelado, o observado simplesmente parece abordar o observador na velocidade v, o que reduz a uma taxa cada vez maior. Em seguida, pára de aproximar-se quando atinge a distância k e, em seguida, acelera-se com uma taxa de aceleração sempre redutora, mas a uma velocidade que continua aumentando até tender para o limite superior v.
Esse comportamento pareceria consistente com a proposição, de que o observador e o observado impõem um ao outro uma força repulsiva, que é inversamente proporcional ao cubo de sua separação.
Interjecção: se os objetos passantes repelissem-se uns aos outros sob da lei do quadrado inverso, a maneira como elétrons passando-se fariam, eles não continuariam em suas respectivas trajetórias retas. Cada um perturbaria o outro, longe de seu curso original, ao longo de uma trajetória hiperbólica.
No entanto, para objetos de passagem neutros, nenhuma força [nem quadrado inverso, nem qualquer outra] está envolvida: apenas velocidades relativas e ângulos. Sem forças; sem 'linhas de mundo'; sem espaço curvo. A força repulsiva é uma ilusão de movimento relativo. Poderiam outras forças repulsivas — como algumas das que estão no mundo subatômico — também serão finalmente resolvidas como ilusões de movimento relativo?
Há um pequeno toque para esse cenário. Para que o observado pareça viajar diretamente para o observador, pare, então, afaste-se novamente, o observador deve girar a sua cabeça (ou a sua direção da vista). Além disso, a taxa em que ele deve mover a sua cabeça, para manter o objeto observado diretamente na linha, não é linear. Ele deve aplicar uma aceleração angular e depois uma desaceleração angular. E isso requer a aplicação de uma força externa especificamente variável sob a forma de torque. Talvez esta aceleração, aparentemente sem força, esteja, de alguma forma, relacionada com um torque de rotação. A aparente força de repulsão, portanto, aparece somente dentro do quadro de referência de um observador que está passando por uma aceleração rotacional apropriada.
Não obstante, se o observador continuasse a olhar para frente em direção a k, o objeto observado pareceria aproximar-se dele, avançar em frente dele e, em seguida, viraria-se novamente, o que lhe pareceria como um caminho de hipérbola - um pouco semelhante, na natureza, ao caminho seguido por uma repelida partícula carregada.
Na maior parte, portanto, a velocidade relativa entre um observador e um observado, dentro de um cenário que não envolve força, não é constante. Existe, no entanto, uma direção no espaço em que a velocidade relativa entre um observador e o seu observado é constante. É quando o observador e o observado estão em um curso de colisão direta. E esta situação única não exige que o observador rote a sua cabeça para manter o objeto observado no centro de sua visão.
Em resumo, portanto, a presença de aceleração relativa não linear, entre dois objetos no espaço livre, não necessariamente exige a aplicação de uma força externa direcionada nem a presença de qualquer "misteriosa ação a distância" ou "distorção no tecido do espaço-tempo". É inteiramente uma conseqüência da geometria euclidiana simples.
Em Queda Livre
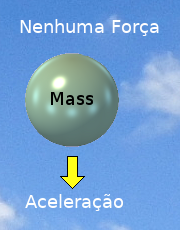 Suponha que eu lance uma massa, como a esfera verde mostrada à esquerda, fora de uma aeronave em vôo. Ele acelerará em direção ao solo a 9,80665 metros por segundo por segundo. No entanto, nenhuma força externa está agindo sobre isso. [Uma força externa deve — por definição — ser aplicada em um ponto único na superfície externa de um corpo, distribuindo-se, na forma de estresses internos expansivas e compressivas, em toda a estrutura material do corpo.] Assim, temos outra situação em que uma massa pode ser acelerada sem que uma força externa atue sobre ela.
Suponha que eu lance uma massa, como a esfera verde mostrada à esquerda, fora de uma aeronave em vôo. Ele acelerará em direção ao solo a 9,80665 metros por segundo por segundo. No entanto, nenhuma força externa está agindo sobre isso. [Uma força externa deve — por definição — ser aplicada em um ponto único na superfície externa de um corpo, distribuindo-se, na forma de estresses internos expansivas e compressivas, em toda a estrutura material do corpo.] Assim, temos outra situação em que uma massa pode ser acelerada sem que uma força externa atue sobre ela.
Não obstante, se trabalharmos para trás a partir da aceleração, usando a observação de Isaac Newton de que força = massa × aceleração para uma força externa dirigida agindo sobre uma massa em espaço livre, pareceria para a nossa percepção humana falível, que algum tipo de força fantasmagórica está agindo sobre a massa em queda.
No entanto, ao contrário de uma força real, que atua em uma massa no espaço livre, essa força fantasmagórica de queda livre não age sobre a superfície externa de um corpo que cai livremente. Nem, assim, cria quaisquer estresses internos expansivas e compressivas dentro da estrutura material do corpo. É como se essa força fantasmagórica fosse infinitamente dividida para que ela atuasse, de forma direta e independente, em cada última molécula, átomo, partícula primária, corda ou qualquer outro constituinte de massa. Então, novamente, não é o mesmo tipo de coisa que uma força externa real.
Expandindo o escopo da minha visão, vejo que a noção de queda livre é, no sentido mais estrito, duas massas caindo umas nas outras: uma sendo a pequena massa que expulso da aeronave e a outra sendo a Terra. Além disso, a taxa em que eles aceleram umas em relação ao outro não é o 9,966565 metros por segundo por segundo: é um tipo complicado de aceleração que é extremamente não linear.
 A força aparente, que parece puxar dois objetos em espaço livre em direção um para outro, é mostrada na ilustração à direita. Essa força aparente fica enormemente mais forte à medida que os 2 objetos se aproximam, conforme mostrado pela fórmula na parte inferior do diagrama. Esta força fictícia parece acelerar os objetos, cada na dirção do outro, em uma taxa cada vez maior.
A força aparente, que parece puxar dois objetos em espaço livre em direção um para outro, é mostrada na ilustração à direita. Essa força aparente fica enormemente mais forte à medida que os 2 objetos se aproximam, conforme mostrado pela fórmula na parte inferior do diagrama. Esta força fictícia parece acelerar os objetos, cada na dirção do outro, em uma taxa cada vez maior.
Observe: esta fórmula é derivada da observação e medição direto e o constante 'G' é extremamente pequeno: 6·67408 × 10−11.
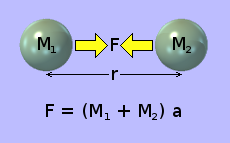 Se essa força fosse uma força real aplicada externamente (o que não é), aceleraria os 2 objetos, cada na dirção a outro, de acordo com a fórmula mostrada à esquerda. Os cientistas tomaram a liberdade duvidosa de considerar a força fantasmagórica de atração entre os dois objetos e a força externa real necessária para produzir a mesma aceleração, para ser equivalente.
Se essa força fosse uma força real aplicada externamente (o que não é), aceleraria os 2 objetos, cada na dirção a outro, de acordo com a fórmula mostrada à esquerda. Os cientistas tomaram a liberdade duvidosa de considerar a força fantasmagórica de atração entre os dois objetos e a força externa real necessária para produzir a mesma aceleração, para ser equivalente.
Observe: esta fórmula é, também, derivada da observação e medição direto.
 Chegam assim a uma fórmula, mostrada à direita, para calcular a aceleração produzida pela assim-chamada atração gravitacional. Supondo que as duas massas envolvidas permanecem constantes, a fórmula reduz para a aceleração, a = K ÷ r2, onde K é uma constante. Do ponto de vista da engenharia, os cientistas são vindicados. A fórmula funciona! E com uma ótima precisão.
Chegam assim a uma fórmula, mostrada à direita, para calcular a aceleração produzida pela assim-chamada atração gravitacional. Supondo que as duas massas envolvidas permanecem constantes, a fórmula reduz para a aceleração, a = K ÷ r2, onde K é uma constante. Do ponto de vista da engenharia, os cientistas são vindicados. A fórmula funciona! E com uma ótima precisão.
Não obstante, de um ponto de vista conceitual, equiparar essa força fictícia de atração com a força real que produziria a mesma aceleração, permanece problemática. Quando um objeto está em queda livre, não há nenhuma força tangível que atua sobre ele. A única situação em que a gravidade exerce uma força tangível é quando um objeto está descansando no chão. Então, o que realmente está acontecendo? Qual é a verdade conceitual?
A aceleração das duas massas, uma para a outra, é extremamente não linear. É inversamente proporcional ao quadrado da distância entre as massas. É interessante lembrar, no entanto, que a aceleração de dois objetos que se passam em um curso sem colisão em espaço livre é inversamente proporcional ao cubo da distância entre os objetos. Então, uma aceleração extemamente não-linear não é grande coisa. Não significa, necessariamente, que alguma força misteriosa esteja envolvida.
A presença de aceleração e a ausência de uma força externa tangível sugerem que, no processo de queda um do outro, as duas massas estão em um estado similar a dois objetos livres em um curso sem colisão em espaço livre. De fato, se uma força externa real for aplicada a um objeto em queda livre, ele irá, de forma independente da aceleração sob queda livre, acelerar exatamente da mesma forma que um objeto em espaço livre distante de qualquer planeta. Vectorialmente, seu movimento sob a influência da força real é simplesmente sobreposto em cima de sua aceleração sob queda livre.
Existe, no entanto, uma diferença crucial. A força externa real tem que superar a inércia inerente do objeto para acelerá-lo. A força fantasmagórica da gravidade não. Quando um objeto está em queda livre, ele não exibe nenhuma reação inercial. Se estiver acelerando assim, e se não for necessária uma força real para manter essa aceleração, parece que, nessa situação, o objeto não possui inércia. Ainda é um objeto material, que presumimos, portanto, deve ter massa. Mas não tem inércia. Isso novamente sugere-me que talvez, na realidade, a inércia não seja propriedade da matéria, mas do espaço.
Em Órbita
Queda-livre - quando dois objetos caem-se um na direção do outro em um curso de colisão direta - é realmente apenas um caso especial de um assim-chamado encontro gravitacional.
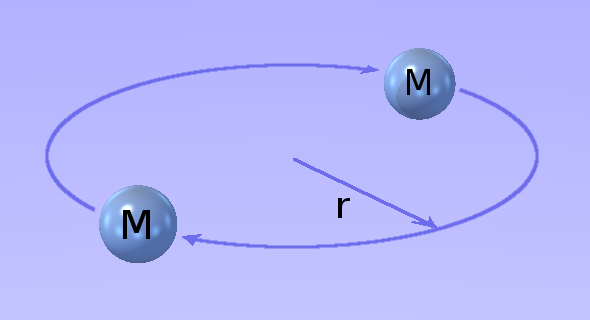
O caso geral é onde dois objetos aproximam-se apartir dos infinitos opostos, passam-se uns aos outros em caminhos não colisão, depois afastam-se, um do outro, em direção dos dois outros infinitos opostos. Os caminhos que seguem são hiperbólicos. Outros casos especiais são onde os caminhos são parabólicos, elípticos e circulares. O caso de dois objetos em órbita circular é mostrado à direita.
 De acordo com a ciência convencional, os 2 objetos em órbita um do outro atraem-se gravitacionalmente com uma força F, que é dada pela fórmula mostrada à esquerda.
De acordo com a ciência convencional, os 2 objetos em órbita um do outro atraem-se gravitacionalmente com uma força F, que é dada pela fórmula mostrada à esquerda.
Por favor, note que, nesta fórmula, R (letra maiúscula) é a distância que separa os dois objetos, que é o dobro do raio da órbita, r (letra minúscula).
Assim, a força fictiva de atração, F = G × (M ÷ (2 × r))² = GM²/4r².
 Em uma órbita circular estável, essa força fictiva de atração é dita ser equilibrada por uma força centrífuga igual e oposta, F, que é dada pela fórmula mostrada à direita. F é a força que puxa um peso para fora quando você o gira em volta em uma corda. Nesta fórmula, ω é a velocidade angular (em radianos por segundo) com a qual estes objetos estão girando em torno de seu centro comum.
Em uma órbita circular estável, essa força fictiva de atração é dita ser equilibrada por uma força centrífuga igual e oposta, F, que é dada pela fórmula mostrada à direita. F é a força que puxa um peso para fora quando você o gira em volta em uma corda. Nesta fórmula, ω é a velocidade angular (em radianos por segundo) com a qual estes objetos estão girando em torno de seu centro comum.
A fórmula acima é essencialmente a mesma observação de Isaac Newton que força = massa × aceleração, mas aplicada ao movimento em um círculo em vez de uma linha reta. A aceleração é a taxa de mudança de velocidade. A velocidade é distância [metros] por unidade de tempo [segundo] em uma linha reta. Força é necessário para mudar a direção no qual um objeto move-se. Portanto, quando um objeto move-se em um círculo, sua velocidade está mudando constantemente [ele está acelerando], mesmo que a taxa com qual ele move-se ao longo do seu caminho orbital - e, portanto, também a sua velocidade angular - permaneçam constantes.
Se essas forças fictícias atraentes e centrífugas são iguais e opostas, então:
| M × r × ω² | = G × M × M ÷ (4 × r × r)
|
| ω² | = G × M ÷ (4 × r × r × r)
|
|---|
| = G × M ÷ (4 × r³)
|
| ω² | = GM/4r³
|
|---|
Assim, a velocidade angular orbital ω dos dois objetos ao redor do centro comum para uma órbita circular estável é dada pela fórmula: ω = √(GM/4r³) radianos por segundo.
Aqui novamente, como com o movimento linear, nenhum dos objetos está sendo submetido a qualquer força externa direcionada. Se um dos objetos fosse um observador consciente, não sentiria nada. Nenhuma agência externa está cutucando ou empurrando o objeto em qualquer direção. Não existe força externa, aplicada em qualquer ponto da sua superfície, sendo distribuída para todas as suas partes através de estresses internos expansivas e compressivas dentro da estrutura do seu material.
E aqui novamente, uma vez que os objetos estão claramente acelerando sem a presença de forças externas para acelerá-los, parece que os dois corpos orbitando uns nos outros não têm inércia. Sem força: sem reação inercial. Mesmo assim, eles estão em um estado de constante aceleração.
Movimento sem Força
Infelizmente, uma educação humana, dentro da biosfera do Planeta Terra, não nos ajuda quando tentamos entender movimento no espaço livre. Dentro da nossa experiência terrestre, nada move-se a menos que seja empurrado. Em outras palavras, sem uma força externa, as coisas simplesmente ficam paradas. E é nessa experiência abrangente que nossos conceitos de movimento são baseados natural e subconscientemente.
Mas fora, no espaço, não funciona assim. No espaço livre, qualquer objeto, que não está sendo agido por uma força externa direcionada, está em repouso. Mas em repouso em relação ao que? A essência - ou substância - do espaço! Tal objeto pode estar em repouso em relação a outros objetos. Poderia ser em movimento a velocidades incríveis em relação aos outros. Poderia até sofrer acelerações extremamente não-lineares em relação a outras. Mas em relação à essência ou substância do espaço, está em repouso. Está estacionário. E o mesmo aplica para todos os outros objetos que não sendo agido por forças externas direcionadas.
A noção de movimento acima descrita - ou melhor, a ausência de tal movimento - em relação à essência ou substância do espaço é bastante estranha à experiência humana diária. No entanto, eu penso o que isso não é muito devido à nossa noção terrestre de movimento, mas sim à nossa concepção terrestre do espaço. Nossa noção básica de espaço, aqui na Terra, é a distância: as separações estáticas entre locais diferentes.
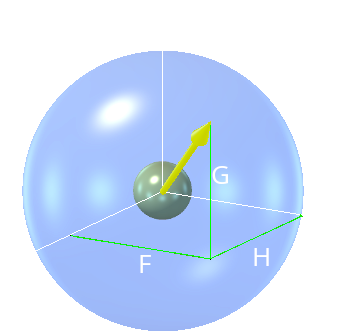 O conceito básico lá fora no espaço livre, no entanto, é força. Um objeto material existe claramente no espaço tridimensional x, y, z. Não obstante, a essência ou substância desse espaço é inconsciente de qualquer estado passivo de movimento que o objeto possa ter em relação a outros objetos. Ela apenas reage — revela a sua existência — quando uma força dirigida é aplicada ao objeto. Assim, pode-se dizer que a essência ou substância do espaço livre existe apenas em uma estrutura-de-referência basiada em força f, g, h, como mostrado na esquerda. E dentro desta estrutura-de-referência f, g, h, a essência ou substância do espaço parece ter a natureza de um fluido viscoso estático.
O conceito básico lá fora no espaço livre, no entanto, é força. Um objeto material existe claramente no espaço tridimensional x, y, z. Não obstante, a essência ou substância desse espaço é inconsciente de qualquer estado passivo de movimento que o objeto possa ter em relação a outros objetos. Ela apenas reage — revela a sua existência — quando uma força dirigida é aplicada ao objeto. Assim, pode-se dizer que a essência ou substância do espaço livre existe apenas em uma estrutura-de-referência basiada em força f, g, h, como mostrado na esquerda. E dentro desta estrutura-de-referência f, g, h, a essência ou substância do espaço parece ter a natureza de um fluido viscoso estático.
Conseqüentemente, se eu estou no espaço livre, longe da visão ou influência de qualquer outro objeto e sem força externa agindo sobre mim, estou em repouso em relação à essência ou substância do espaço. Da mesma forma, se eu estiver acelerando a queda livre em direção a um planeta, novamente sem força externa agindo sobre mim, também estou em repouso em relação à essência ou substância do espaço.
O espaço tem tamanho. Portanto, não pode ser "nada". Portanto, deve ter essência ou substância de algum tipo. Eu chamo de essência ou substância do espaço o éter. Imagino que o éter tenha a natureza de um fluido; especificamente, o que eu chamo de 'fluido de velocidade'. O espaço contém objetos. Esses objetos têm movimentos relativos muito complexos. No entanto, cada um — sobre o qual nenhuma força externa dirigida está agindo — está em repouso em relação ao éter.
Para conciliar a noção de objetos sendo em movimento em relação um ao outro no espaço x, y, z, com a noção de cada um sendo em repouso em relação ao éter, o próprio éter deve estar em um estado contínuo de movimento. Deve ser, em diferentes momentos em diferentes lugares, se expandindo, contraindo, torcendo e dobrando.
Alternativamente, pode-se supor que é o éter que está parado e homogêneo e que é o espaço x, y, z que está se expandindo, contraindo, torcendo e dobrando.
E tudo isso ocorre sem a ação de forças externas. O movimento passivo complexo é simplesmente o estado fundamental do universo.
© 26 abril 2016 Robert John Morton |
ANTE |
PROX

 Em uma noite tropical clara, fora no campo longe das luzes da cidade, adoro olhar para o céu. Eu vejo, em várias ocasiões, a Via Láctea, a Cruz do Sul e o Orion com Betelgeuse na esquina. Tudo parece majestoso, pacífico e imóvel. Mas na realidade, todas as estrelas estão em movimento constante em relação umas com as outras. Betelgeuse é tão grande que, se fosse onde o sol está, engoliria todos os planetas internos dentro de sua superfície contorcida. Mesmo o tamanho e a forma da nebulosa gigante à direita, conhecida como a Mão de Deus, está mudando constantemente. As galáxias todas rodam e traduzem-se umas com as outras, assim como fazem moléculas e átomos.
Em uma noite tropical clara, fora no campo longe das luzes da cidade, adoro olhar para o céu. Eu vejo, em várias ocasiões, a Via Láctea, a Cruz do Sul e o Orion com Betelgeuse na esquina. Tudo parece majestoso, pacífico e imóvel. Mas na realidade, todas as estrelas estão em movimento constante em relação umas com as outras. Betelgeuse é tão grande que, se fosse onde o sol está, engoliria todos os planetas internos dentro de sua superfície contorcida. Mesmo o tamanho e a forma da nebulosa gigante à direita, conhecida como a Mão de Deus, está mudando constantemente. As galáxias todas rodam e traduzem-se umas com as outras, assim como fazem moléculas e átomos.
 Quando criança, eu familiarizei-me com muitos tipos diferentes de coisas que se movem, que eu encontrei principalmente na casa de meus avós e ao redor dela. No entanto, penso que a primeira coisa, que eu mentalmente abstrai como um objeto móvel independente, era uma bola suave com a qual eu jogava no jardim dos meus avós.
Quando criança, eu familiarizei-me com muitos tipos diferentes de coisas que se movem, que eu encontrei principalmente na casa de meus avós e ao redor dela. No entanto, penso que a primeira coisa, que eu mentalmente abstrai como um objeto móvel independente, era uma bola suave com a qual eu jogava no jardim dos meus avós.
 O diagrama à esquerda mostra um objeto que viaja através do espaço vazio ao longo do eixo dos x em uma velocidade v dentro do quadro de referência de um observador. O objeto passará mais próximo do observador a uma distância k. O observador vê o objeto vindo para ele como se fosse diretamente ao longo da pista hipotenusa r. Para o observador, o objeto parece estar se movendo em direção a ele a uma velocidade cada vez menor.
O diagrama à esquerda mostra um objeto que viaja através do espaço vazio ao longo do eixo dos x em uma velocidade v dentro do quadro de referência de um observador. O objeto passará mais próximo do observador a uma distância k. O observador vê o objeto vindo para ele como se fosse diretamente ao longo da pista hipotenusa r. Para o observador, o objeto parece estar se movendo em direção a ele a uma velocidade cada vez menor.
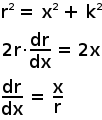 No triângulo mostrado acima, k é constante, enquanto x e r diminuem com o tempo. Como k é a distância de abordagem mais próxima, o triângulo tem ângulo de 90°. Os lados x, r e k são, portanto, relacionados pela regra dos quadrados de Pitágoras, como mostrado à direita. Como k é constante, a taxa em que r muda com x pode ser calculada por diferenciar a equação de Pitágoras como mostrado à direita.
No triângulo mostrado acima, k é constante, enquanto x e r diminuem com o tempo. Como k é a distância de abordagem mais próxima, o triângulo tem ângulo de 90°. Os lados x, r e k são, portanto, relacionados pela regra dos quadrados de Pitágoras, como mostrado à direita. Como k é constante, a taxa em que r muda com x pode ser calculada por diferenciar a equação de Pitágoras como mostrado à direita.
 Usar a regra de cadeia para diferenciação, agora podemos descobrir como a distância r varia ao longo do tempo. O diferencial de x em relação ao tempo é a velocidade v do objeto ao longo do eixo dos x. Isso nós consideramos constante porque decretamos que o objeto viaja ao longo de seu caminho a velocidade constante. Nenhuma força está agindo sobre isso.
Usar a regra de cadeia para diferenciação, agora podemos descobrir como a distância r varia ao longo do tempo. O diferencial de x em relação ao tempo é a velocidade v do objeto ao longo do eixo dos x. Isso nós consideramos constante porque decretamos que o objeto viaja ao longo de seu caminho a velocidade constante. Nenhuma força está agindo sobre isso.
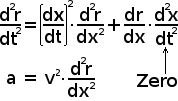 A tarefa agora é descobrir se, e se assim for, por quanto, o objeto está acelerando, ao longo do caminho r, em direção ao observador. Usando a regra padrão para calcular a segunda derivada, encontramos que o segundo termo é zero porque decretamos que a velocidade, v, do objeto ao longo do eixo x seja constante.
A tarefa agora é descobrir se, e se assim for, por quanto, o objeto está acelerando, ao longo do caminho r, em direção ao observador. Usando a regra padrão para calcular a segunda derivada, encontramos que o segundo termo é zero porque decretamos que a velocidade, v, do objeto ao longo do eixo x seja constante.
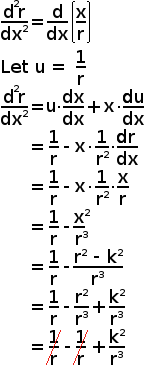 Para completar o cálculo da aceleração, a, ao longo de r, devemos avaliar a segunda derivada de r em relação a x. Esta é efetivamente a derivada da primeira derivada de r em relação a x, que descobrimos ser x / r. Em vez de lidar com o recíproco de r, prefiro substituir uma nova variável u = 1 / r. Então o problema se torna diferenciar o produto das duas variáveis relacionadas x e u.
Para completar o cálculo da aceleração, a, ao longo de r, devemos avaliar a segunda derivada de r em relação a x. Esta é efetivamente a derivada da primeira derivada de r em relação a x, que descobrimos ser x / r. Em vez de lidar com o recíproco de r, prefiro substituir uma nova variável u = 1 / r. Então o problema se torna diferenciar o produto das duas variáveis relacionadas x e u.
 Suponha que eu lance uma massa, como a esfera verde mostrada à esquerda, fora de uma aeronave em vôo. Ele acelerará em direção ao solo a 9,80665 metros por segundo por segundo. No entanto, nenhuma força externa está agindo sobre isso. [Uma força externa deve — por definição — ser aplicada em um ponto único na superfície externa de um corpo, distribuindo-se, na forma de estresses internos expansivas e compressivas, em toda a estrutura material do corpo.] Assim, temos outra situação em que uma massa pode ser acelerada sem que uma força externa atue sobre ela.
Suponha que eu lance uma massa, como a esfera verde mostrada à esquerda, fora de uma aeronave em vôo. Ele acelerará em direção ao solo a 9,80665 metros por segundo por segundo. No entanto, nenhuma força externa está agindo sobre isso. [Uma força externa deve — por definição — ser aplicada em um ponto único na superfície externa de um corpo, distribuindo-se, na forma de estresses internos expansivas e compressivas, em toda a estrutura material do corpo.] Assim, temos outra situação em que uma massa pode ser acelerada sem que uma força externa atue sobre ela.
 A força aparente, que parece puxar dois objetos em espaço livre em direção um para outro, é mostrada na ilustração à direita. Essa força aparente fica enormemente mais forte à medida que os 2 objetos se aproximam, conforme mostrado pela fórmula na parte inferior do diagrama. Esta força fictícia parece acelerar os objetos, cada na dirção do outro, em uma taxa cada vez maior.
A força aparente, que parece puxar dois objetos em espaço livre em direção um para outro, é mostrada na ilustração à direita. Essa força aparente fica enormemente mais forte à medida que os 2 objetos se aproximam, conforme mostrado pela fórmula na parte inferior do diagrama. Esta força fictícia parece acelerar os objetos, cada na dirção do outro, em uma taxa cada vez maior.
 Se essa força fosse uma força real aplicada externamente (o que não é), aceleraria os 2 objetos, cada na dirção a outro, de acordo com a fórmula mostrada à esquerda. Os cientistas tomaram a liberdade duvidosa de considerar a força fantasmagórica de atração entre os dois objetos e a força externa real necessária para produzir a mesma aceleração, para ser equivalente.
Se essa força fosse uma força real aplicada externamente (o que não é), aceleraria os 2 objetos, cada na dirção a outro, de acordo com a fórmula mostrada à esquerda. Os cientistas tomaram a liberdade duvidosa de considerar a força fantasmagórica de atração entre os dois objetos e a força externa real necessária para produzir a mesma aceleração, para ser equivalente.
 Chegam assim a uma fórmula, mostrada à direita, para calcular a aceleração produzida pela assim-chamada atração gravitacional. Supondo que as duas massas envolvidas permanecem constantes, a fórmula reduz para a aceleração, a = K ÷ r2, onde K é uma constante. Do ponto de vista da engenharia, os cientistas são vindicados. A fórmula funciona! E com uma ótima precisão.
Chegam assim a uma fórmula, mostrada à direita, para calcular a aceleração produzida pela assim-chamada atração gravitacional. Supondo que as duas massas envolvidas permanecem constantes, a fórmula reduz para a aceleração, a = K ÷ r2, onde K é uma constante. Do ponto de vista da engenharia, os cientistas são vindicados. A fórmula funciona! E com uma ótima precisão.

 De acordo com a ciência convencional, os 2 objetos em órbita um do outro atraem-se gravitacionalmente com uma força F, que é dada pela fórmula mostrada à esquerda.
De acordo com a ciência convencional, os 2 objetos em órbita um do outro atraem-se gravitacionalmente com uma força F, que é dada pela fórmula mostrada à esquerda.
 Em uma órbita circular estável, essa força fictiva de atração é dita ser equilibrada por uma força centrífuga igual e oposta, F, que é dada pela fórmula mostrada à direita. F é a força que puxa um peso para fora quando você o gira em volta em uma corda. Nesta fórmula, ω é a velocidade angular (em radianos por segundo) com a qual estes objetos estão girando em torno de seu centro comum.
Em uma órbita circular estável, essa força fictiva de atração é dita ser equilibrada por uma força centrífuga igual e oposta, F, que é dada pela fórmula mostrada à direita. F é a força que puxa um peso para fora quando você o gira em volta em uma corda. Nesta fórmula, ω é a velocidade angular (em radianos por segundo) com a qual estes objetos estão girando em torno de seu centro comum.
 O conceito básico lá fora no espaço livre, no entanto, é força. Um objeto material existe claramente no espaço tridimensional x, y, z. Não obstante, a essência ou substância desse espaço é inconsciente de qualquer estado passivo de movimento que o objeto possa ter em relação a outros objetos. Ela apenas reage — revela a sua existência — quando uma força dirigida é aplicada ao objeto. Assim, pode-se dizer que a essência ou substância do espaço livre existe apenas em uma estrutura-de-referência basiada em força f, g, h, como mostrado na esquerda. E dentro desta estrutura-de-referência f, g, h, a essência ou substância do espaço parece ter a natureza de um fluido viscoso estático.
O conceito básico lá fora no espaço livre, no entanto, é força. Um objeto material existe claramente no espaço tridimensional x, y, z. Não obstante, a essência ou substância desse espaço é inconsciente de qualquer estado passivo de movimento que o objeto possa ter em relação a outros objetos. Ela apenas reage — revela a sua existência — quando uma força dirigida é aplicada ao objeto. Assim, pode-se dizer que a essência ou substância do espaço livre existe apenas em uma estrutura-de-referência basiada em força f, g, h, como mostrado na esquerda. E dentro desta estrutura-de-referência f, g, h, a essência ou substância do espaço parece ter a natureza de um fluido viscoso estático.