Herein I describe the computations that need to be done to track the moon in real time to within a couple of minutes of arc. I conclude with a philosophical note about the real laws of physics and the limitations of the language of mathematics we use to try to get a handle of understanding on them.
The C-function that performs these computations is part of the program com.c. Click on the link and display the program in a text editor with programmer's highlighting such as 'gedit'. Then scan for the function name T7moon().

The function T7moon() performs the moon tracking computations, the results of which are displayed and updated once per second in the MOON tab's TRACK sub-tab as shown above. The final output is the current azimuth and elevation of the Moon from the point of view of the Base Station coordinates. These are sent via stdout to the antenna steering servos. A description of each of the series of computations required to achieve the final output is described below.
Compute The Julian Day Number
The Julian Day number is the real number of 24-hour days measured from the most recent Julian Epoch. It is expressed as an integral + a fractional part of a day, which is generally updated once per second. Consequently, the current Julian Day number specifies an elapsed period of time to a precision of one second.
The most recent Julian Epoch at the time of writing started at 00h00m00s GMT on Saturday 01 January 2000.
A Julian Day is an artificial Standard Day deemed to comprise exactly 24 standard hours. A real day doesn't. A real day varies in length capriciously throughout a year and indeed in the longer term. Thus a long period measured in Julian days does not correspond to the same count of real days.
The name 'Julian' is historical but is nowadays, to my mind, a bit confusing. Being named after Julius Caesar, it gives the sense of something ancient. However, it is now defined in terms of Universal Time [Greenwich Mean Time], which is derived from an atomic clock. I therefore think that a more appropriate name for the Julian Day would be the Atomic Day.
A Julian Day is, by convention, measured from noon to noon: not midnight to midnight like normal days. However, for the purpose of the following astronomical computations, it is more convenient if they run from midnight to midnight, so that's how they're treated in this program.
A number of Julian Days is always measured from the start of a Julian Epoch. This is an agreed point in time at which astronomical fixes of lunar and solar orbital positions are taken in order to provide the initial starting constants for measuring a long period of time.
With reference to the time now, the whole number of [completed] Julian days 'jd', that has elapsed since 00h00m00s GMT on 01 January 2000, is computed by a formula of convention. The one used in this program is:
jd = 367 × yyyy
− 7 × ( yyyy + (mm + 9) ÷ 12 ) ÷ 4
− 3 × ( ( yyyy + (mm − 9) ÷ 7 ) ÷ 100 + 1 ) ÷ 4
+ 275 × mm ÷ 9
+ dd
− 730515;
This formula refers back to the start of what is called the Julian Period [which began at noon on Monday 01 January 4713 BC] in order to compute the number of days that has elapsed in the current Julian Epoch. The remaining fractional part of the Julian Day is computed separately by reference to Greenwich Mean Time given in seconds past midnight. The complete Julian Day number 'JD' is given by:
[integral+fractional] number of days since 00:00 GMT 01 Jan 2000
| whole days since 00:00:00 GMT 01 Jan 2000
| | GMT now in seconds since midnight
| | | seconds in a day = 24 × 60 × 60
| | | | */
double JD = ((double)jd + (double)gms / 86400.0), // in 24-hour days
For a full explanation of the Julian Day please see Wikipedia article. It's complicated. The Julian Day number is used in this program to compute the current orbital position of the Moon on the Celestial Sphere.
Compute Earth-Moon Distance & True Anomaly
There are three kinds of anomaly [angle] that must be computed for the Moon:
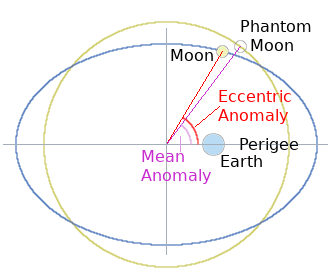
- The Moon's Mean Anomaly [Mm]
- The Moon's Eccentric Anomaly [Em]
- The Moon's True Anomaly [Vm]
The Moon's Mean Anomaly is the fraction of a Sidereal Month [the Moon's true orbital period in space] that has [at the present point in time] elapsed since the Moon last passed its perigee. It does not follow the true track of the Moon around its orbit. It follows a phantom Moon that follows a circular orbit at constant angular speed so as to finish each orbit in exactly one Sidereal Month.
The real Moon and the phantom Moon always start off a new Sidereal Month lined up on the moon's perigee [where the Moon is closest to the Earth]. Initially the real Moon pulls away faster than the phantom Moon around its orbit but later starts to slow down until both of them are in line again at the apogee [where the Moon is furthest from the Earth]. Then, in the second half of the month, the real Moon starts to lag behind the phantom Moon, later increasing its speed to catch up so that both are in line again at the perigee.
The phantom Moon travels around its circular orbit at 0·2280271437424892 radians per Julian Day. So the number of radians swept by the phantom Moon around its orbit since the start of the present Julian Epoch [00h00 on 01 January 2000] is this figure times the number of Julian Days [including the final fraction of a Julian Day] that has elapsed since the start of the Epoch.
But at 00h00 on 01 January 2000, the phantom moon was already 2·0135060729 radians beyond the real Moon's last perigee. So this has to be added on to find the total number of radians swept.
However, we are not interested in this enormous angular sweep since the beginning of the latest Julian Epoch. We are only interested in the current fraction of the orbit that has been swept since the last perigee encounter. So we take off all complete orbits leaving only the current fractional orbit. The function 'RatAng()' in the program takes off all completed turns of 2π radians to leave just the fraction of the orbit in radians that has been completed from the last perigee encounter up to the time 'now'. This is the Moon's Mean Anomaly, which is designated 'Mm'.
The Moon's Eccentric Anomaly [designated 'Em'] is the angle that defines the instantaneous position of the real Moon moving along its elliptical orbit around the Earth. This is computed by Keppler's equation: Mm = Em − 0·0549 × sin(Em), where 0·0549 is the eccentricity of the Moon's elliptical orbit. However, in order to calculate the value of Em explicitly, we must re-cast Kepler's equation into the form:
Em = Mm + 0·0549 × sin(Mm) × (1·0 + 0·0549 × cos(Mm))
The geometrical relationship between mean Anomaly and Eccentric Anomaly is illustrated above on the right.
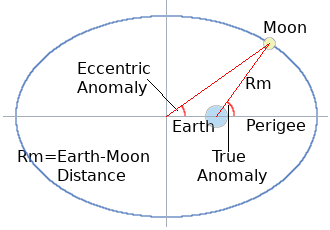 The Moon's True Anomaly [which is designated 'Vm'] is the angle between the line of perigee and the current position of the Moon, as seen from the main focus of the ellipse [the point around which it orbits]. This point is of course the centre of the Earth.
The Moon's True Anomaly [which is designated 'Vm'] is the angle between the line of perigee and the current position of the Moon, as seen from the main focus of the ellipse [the point around which it orbits]. This point is of course the centre of the Earth.
The adjacent diagram shows the geometrical relationship between the Moon's Eccentric Anomaly and its True Anomaly.
In order to derive the Moon's True Anomaly from its Eccentric Anomaly, it is necessary to express the moon's position relative to the Earth in terms of Cartesian coordinates whose origin is at the centre of the Earth, with the X-axis running along the major axis of the elliptical orbit of the Moon. In the diagram, the moon orbits counter-clockwise, as per mathematical convention.
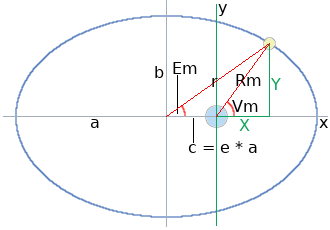
X = Rm × cos(Vm)
= a × (cos(Em) − e)
Y = Rm × sin(Vm)
= a × (√(1 − e²) × sin(Em))
a = 60.2666 Earth-radii
e = 0.0549 [a ratio]
a × √(1 − e²) = 60.175709409
X = 60.2666 × (cos(Em) − 0.0549)
Y = 60.175709409 × sin(Em)
The Moon's True Anomaly, Vm = atan2(X,Y) [in radians].
The Earth-Moon distance, Rm = √(X² + Y²) [in Earth-radii].
Compute Moon's Argument of Perigee
Thus far, we have been dealing with the Moon's motion within the plane of its own orbit. We must now convert the Moon's position within that frame of reference into the frame of reference of the Ecliptic Plane: that is, the plane of the Earth's orbit around the Sun.
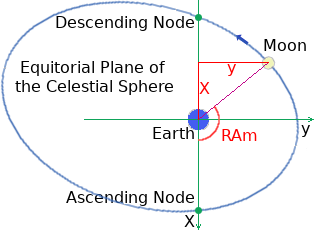
The Nodes [red blobs in the diagram below] are the points at which the Moon's Orbit crosses [punches through] the Ecliptic Plane. The Descending Node is where the Moon crosses from North to South. The Ascending Node is where the Moon crosses from South to North. The line [also shown in green], which joins the Moon's Descending Node and Ascending node, is the line of intersection between the Moon's Orbital Plane and the Ecliptic Plane.
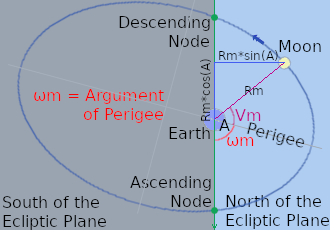
The Moon's Argument of Perigee, 'wm' is the angle [shown in red in the diagram] between the Moon's Line of Perigee and the line joining the two nodes. The direction from the point of view of the Earth to the Ascending Node of the Moon's orbit is the reference direction for arbitrarily defining the orientation in space of the Moon's elliptical orbit.
The Moon's Argument of Perigee 'ωm' is not constant. It changes with time.
It is computed by starting from its value at the beginning of the current Julian Epoch, when it was accurately determined astronomically, and then adding the angular extent it has swept during the time since then until 'now'. This extra swept angle is the number of Julian Days [including the final fraction of a Julian Day] multiplied by the Moon's mean angular velocity [in radians per Julian Day]. This is an enormous angle, so we take off all the completed orbits [turns of 2π radians], leaving only the remaining fraction of an orbit. This remaining fraction is the Moon's current Argument of Perigee, 'ωm'.
compute 'ωm' the Moon's ARGUMENT OF PERIGEE, which is the angle between
the direction of the ascending node and the direction of the perigee.
| value of 'ωm' at 00h00 GMT 01 January 2000
| | average number of radians per day orbital speed
| | |
ωm = RatAng(5·5512535601 + 0·00286857642388938 * JD)
| |
chops off all the Number of Julian Days elapsed
completed orbits since 00h00 GMT 01 January 2000
In this new coordinate system, we need the angular displacement of the Moon from the direction of the Moon's Ascending Node. I shall call it 'A'.
From the above diagram A = ωm + Vm [where Vm is the Moon's True Anomaly]
The Moon's Orbital Plane intersects the Ecliptic Plane at an angle of 0·0898041713 radians. This can be confidently regarded as a constant.
Geocentric Cartesian Frame of The Ecliptic Plane
The Ecliptic Plane is the plane of the Earth's orbit around the Sun. However, in the coordinate system we will use in the Ecliptic Plane is necessarily Earth-centred: the common zero-point of the x, y, z axes is the centre of the Earth: not the Sun. The reason we are using the Ecliptic Plane as the coordinate reference here is because, later, we will have to include perturbations to the Moon's position resulting from the gravitational influence of the Sun. These perturbations are not insignificant.
The X,Y,Z axes of the Cartesian frame based on the Ecliptic Plane has its origin at the centre of the Earth. The 'X' and 'Y' axes are within the Ecliptic Plane. The 'Z' axis is perpendicular to the Ecliptic Plane through the centre of the Earth. The 'Z' axis may be considered to be the 'polar' axis of the Ecliptic Sphere, which is like the Celestial Sphere tilted by the angle of the Earth's axial tilt of 23·5°.
The angle between the Earth-Moon orbital radius 'R' and the diagonal 'D' in the following diagram is the angle of intersection between the plane of the Moon's orbit around the Earth and the Ecliptic Plane. This is 5°. It has been highly exaggerated in the diagram for geometric clarity.
To make the following diagrams less cramped, I have had to make the angle 'A' obtuse. So to keep track of the signs of terms in the following derivation, it is necessary to bear in mind that sin(π − A) ≡ sin(A) and that cos(π − A) ≡ −cos(A).
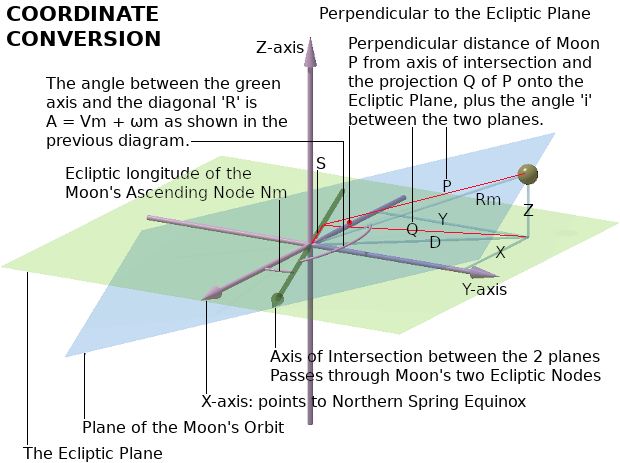
The orientation in space of the 'Z' axis is thus established as the line that passes through the centre of the Earth, perpendicular to the Ecliptic Plane. However, we now need to give an absolute fix for the 'X' and 'Y' axes. We do this by decreeing that the 'X' axis points in the direction of the radial line through the zero meridian of the Celestial Sphere. This line points to the Vernal Equinox [The Spring Equinox of the Northern Hemisphere], where the Sun crosses the Celestial Equator [punches through the Celestial Equatorial Plane] from South to North.
Ecliptic Longitude of Moon's Ascending Node
To relate the Moon's position in its orbit to the Geocentric Frame of the Ecliptic Plane, we need to know the angle between the X-axis and the green line in the above diagram. This angle is known as the Ecliptic longitude of the Moon's Ascending Node. It is designated 'Nm' and is computed as follows:
Compute the ECLIPTIC LONGITUDE 'Nm' of the Moon's Ascending Node: the point
in the Moon's orbit at which the Moon moves into the northern ecliptic hemi-
sphere: i.e. where the Moon's orbit crosses the ecliptic from South to North
|
| longitude of the Moon's ascending Node at 00:00 GMT 01 Jan 2000
| | change in longitude per 24 hour day
| | |
Nm = RatAng(2·1838048293 - 0·000924218306302609 * JD) radians
| |
chops off all the Number of Julian Days elapsed
completed orbits since 00h00 GMT 01 January 2000
Nm varies continually with the motion of the moon round its orbit.
Compute Moon's Ecliptic X,Y,Z Coordinates
Remember that A = ωm + Vm [where Vm is the Moon's True Anomaly].
From the above 3-dimensional diagram, we can see that Z, the height of the Moon above the Ecliptic Plane, is the easiest to compute:
P = Rm × sin(A) and
Z = P × sin(i) so
Z = Rm × sin(A) × sin(i)
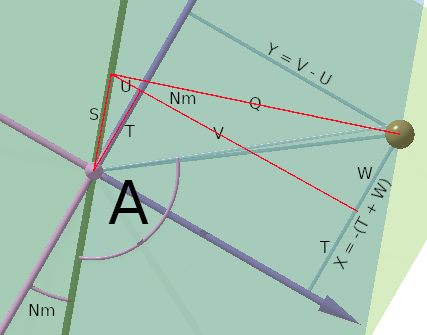 The adjacent diagram is a 2-D part of the above 3-D diagram. It looks from the Ecliptic North directly on to the Ecliptic Plane. The Moon within the lunar Orbital Plane is tilted upwards towards the viewer. From the lettered sides and angles in the diagram, the Moon's Ecliptic X and Y-coordinates can now be derived as follows.
The adjacent diagram is a 2-D part of the above 3-D diagram. It looks from the Ecliptic North directly on to the Ecliptic Plane. The Moon within the lunar Orbital Plane is tilted upwards towards the viewer. From the lettered sides and angles in the diagram, the Moon's Ecliptic X and Y-coordinates can now be derived as follows.
P = Rm × sin(π − A)
S = Rm × cos(π − A)
Q = P × cos(i)
U = S × sin(Nm)
V = Q × cos(Nm)
T = S × cos(Nm)
W = Q × sin(Nm)
X = −(T + W) [T and W are in the negative X-direction on the diagram]
= −(S × cos(Nm) + Q × cos(Nm))
= −(Rm × cos(π − A) × cos(Nm) + Rm × sin(π − A) × cos(i) × sin(Nm))
= −(−Rm × cos(A) × cos(Nm) + Rm × sin(A) × cos(i) × sin(Nm))
= + Rm * cos(A) × cos(Nm) − Rm × sin(A) × cos(i) × sin(Nm))
= Rm × (cos(Nm) × cos(A) − sin(Nm) × sin(A) × cos(i))
Y = V − U [V and U are in the positive Y-direction on the diagram]
= Rm × sin(π − A) × cos(i) × cos(Nm) − Rm × cos(π − A) × sin(Nm)
= Rm × (sin(π − A) × cos(i) × cos(Nm) − cos(π − A) × sin(Nm))
= Rm × (sin(A) × cos(i) × cos(mN) + cos(A) × sin(Nm))
= Rm × (sin(Nm) × cos(A) + cos(Nm) × sin(A) × cos(i))
Please remember that in the diagram, 'A' is obtuse, consequently cos(A) is negative. This causes the length 'U' to be negative. Thus 'U' is effectively an added positive value, whereas T & W are effectively negative amounts.
Compute Moon's Ecliptic Latitude & Longitude
 These are not the same as terrestrial [normal] latitude and longitude. Terrestrial latitude and longitude are specified with reference to the equatorial plane of the Earth. Ecliptic latitude and longitude are specified with reference to the Ecliptic Plane.
These are not the same as terrestrial [normal] latitude and longitude. Terrestrial latitude and longitude are specified with reference to the equatorial plane of the Earth. Ecliptic latitude and longitude are specified with reference to the Ecliptic Plane.
From the diagram, you can see geometrically that the Ecliptic latitude and longitude of the Moon are given by:
LatEcl = atan2(Z,√(X² + Y²))
LngEcl = atan2(Y,X)
Note that, in the diagram, X is negative. The atan2() function will therefore return the obtuse angle of the Moon's Ecliptic longitude as illustrated.
Position of The Sun
We now need to formalise some parameters pertaining to the Sun. These are expressed in terms of the 'orbit' of the Sun around the Earth within the Ecliptic Plane.
This raises a philosophical point about the relativity of observation. We realise that a Heliocentric [Sun-centred] view of the orbits of the Earth, Moon and planets is much simpler when viewed by a hypothetical observer located at the centre of the Sun. Notwithstanding, in a relativistic universe the view of any specific observer is equally valid in physics as that of any other observer. So our Geocentric [Earth-centred] view here is just as valid as any other. It's just a little more complicated, especially when viewing the orbits of the planets.
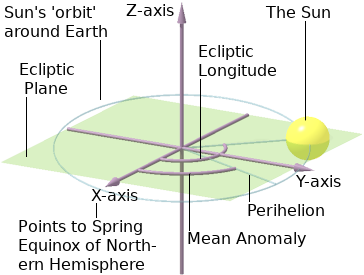 Thus, to express the position of the Sun at any given time, we consider its position upon the Ecliptic Sphere. The Ecliptic Sphere is a sphere containing the Earth [I imagine it as a transparent sphere with latitude and longitude lines marked upon its surface such that the axis joining its poles is the Z-axis in our Cartesian [X,Y,Z] coordinates for the Ecliptic Plane. The axis of the Ecliptic Sphere is thus tilted 23·5° from that of the Celestial Sphere. The Earth is at the origin of the Ecliptic Cartesian coordinates. The Ecliptic X-Y Plane slices the Sun and the Earth in half.
Thus, to express the position of the Sun at any given time, we consider its position upon the Ecliptic Sphere. The Ecliptic Sphere is a sphere containing the Earth [I imagine it as a transparent sphere with latitude and longitude lines marked upon its surface such that the axis joining its poles is the Z-axis in our Cartesian [X,Y,Z] coordinates for the Ecliptic Plane. The axis of the Ecliptic Sphere is thus tilted 23·5° from that of the Celestial Sphere. The Earth is at the origin of the Ecliptic Cartesian coordinates. The Ecliptic X-Y Plane slices the Sun and the Earth in half.
We need to compute the Mean Anomaly of the Sun [Ms] and also its Ecliptic Longitude [Ls] as illustrated in the above diagram.
Ecliptic longitude of the Sun
| Mean Anomaly of the Sun
| | Starting point at 00h00 on 01 January 2000
| | | Angular velocity of Sun's Mean Anomaly
| | | | in Radians per Julian Day
| | | |
| Ms = 6·214192442 + 0·0172019696192896 * JD
| | |
| | The Sun's Argument of Perihelion Julian Day number
| | |
| | ---------------------------------
Ls = Ms + 4·9382415669 + 8·21936631E−7 * JD
| | |
| Angular velocity of Julian Day number
| Sun's Perihelion in
| Radians per Julian Day
|
Starting point at 00h00 on 01 January 2000
We don't need to add the angle of the Sun's Ascending Node because it is zero: it is the sidereal reference direction: the direction of the Northern Hemisphere's Spring Equinox. The Sun's Ecliptic Longitude will also be used later for computing current Greenwich Mean Sidereal Time.
Add Lunar Perturbations
The Moon's orbital position relative to the Earth is, almost entirely, determined by the gravitational influence of the Earth itself. However, the gravitational influence of the Sun also perturbs the Moon in its orbit. Though the Moon be perturbed only slightly by the Sun, these perturbations are by no means insignificant. The terms of these perturbations are many and complicated. The constants are simply the results of empirical observations.
Mean Ecliptic Longitude of the Moon [not True Ecliptic Longitude]
| Moon's Mean Anomaly
| | Moon's Argument of Perigee
| | | Longitude of the Moon's node
| | | |
Lm = Mm + wm + Nm
D = Lm − Ls Mean Elongation of the Moon
F = Lm − Nm Moon's Argument of latitude
In order to avoid having to re-compute what has already been computed, we create the following variables for the following perturbation formulae.
E = D + D Twice the Elongation of the Moon
M = Mm + Ms Sum of the Mean Anomalies of the Sun and Moon
N = Mm − E Moon's Mean Anomaly less twice its Elongation
G = F − E Moon's Argument of Latitude less twice its Elongation
Now we are ready to add the Sun's perturbations of the Moon to the Moon's current True Ecliptic Longitude, Latitude and Radial Distance from the Earth.
Moon's current Ecliptic Longitude [in radians]
|
LngEcl += − 0·022235495 × sin(N) known as The Evection
+ 0·011484266 × sin(E) known as The Variation
− 0·003246312 × sin(Ms) known as The Yearly Equation
− 0·001029744 × sin(Mm + Mm − E)
− 0·000994838 × sin(M − E)
+ 0·000925025 × sin(Mm + E)
+ 0·000802851 × sin(E − Ms)
+ 0·000715585 × sin(Mm − Ms)
− 0·000610865 × sin(D) known as The Parallactic Equation
− 0·000541052 × sin(M)
− 0·000261799 × sin(F + G)
+ 0·000191986 × sin(N − E);
Moon's current Ecliptic Latitude [in radians]
|
LatEcl += − 0·003019420 × sin(F − E)
− 0·000959931 × sin(Mm − F − E)
− 0·000802851 × sin(Mm + F − E)
+ 0·000575959 × sin(F + E)
+ 0·000296706 × sin(Mm + Mm + F);
Earth-Moon Distance [in Earth radii]
|
Rm −= 0·58 × cos(N) + 0.46 × cos(E);
 For a positional accuracy better than 2 arc minutes, all the above terms must be added. These are all aspects of the way in which the gravitational influence of the Sun perturbs the position of the Moon, as typified in the adjacent diagram.
For a positional accuracy better than 2 arc minutes, all the above terms must be added. These are all aspects of the way in which the gravitational influence of the Sun perturbs the position of the Moon, as typified in the adjacent diagram.
All the constants involved are derived from practical empirical observations and the derived terms are added respectively to the Ecliptic Latitude and Ecliptic Longitude of the Moon and the Earth-moon distance.
Re-Compute Moon's Ecliptic Coordinates
It is now necessary to re-compute the geocentric Cartesian coordinates of the moon based on the ecliptic plane after having added the above perturbations. By referring to the above diagram, we can see that:
X = Rm × cos(LngEcl) × cos(LatEcl) x-coord [in the Ecliptic plane]
Y = Rm × sin(LngEcl) × cos(LatEcl) y-coord [in the Ecliptic plane]
Z = Rm × sin(LatEcl) z-coord [perpendicular to it]
Angle Between Ecliptic & Equatorial Planes
We must now compute the Obliquity of the Ecliptic 'o'. This is the angle of intersection between the Ecliptic Plane and the Earth's Equatorial Plane. It is the same as the Earth's Axial Tilt. Its value is about 23·5° [0·4101524 radians] and it is currently decreasing 0·013 degrees [47 arc-seconds or 0·000227862 radians] per hundred years, which is 6·2186081×10−9 radians per Julian Day.
OBLIQUITY OF THE ECLIPTIC [current tilt of Earth's axis to Ecliptic Plane]
| tilt of Earth's axis of rotation at 00:00 GMT 01 Jan 2000
| | tilt reduction per 24-hour day [very small]
| | | Times the number of Julian Days
| | | |
o = RatAng(0·4090929594 - 6·2186081E-9 * JD) in radians
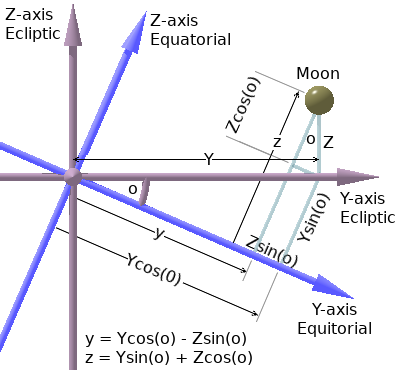 Now convert the Moon's Earth-centred X, Y and Z coordinates based on the Ecliptic Plane to Earth-centred X, y, z coordinates based on the Earth's Equatorial Plane, which is the same as the Equatorial Plane of the Celestial Sphere.
Now convert the Moon's Earth-centred X, Y and Z coordinates based on the Ecliptic Plane to Earth-centred X, y, z coordinates based on the Earth's Equatorial Plane, which is the same as the Equatorial Plane of the Celestial Sphere.
The X-axis is common to both coordinate frames because it is the line of intersection between the two planes. The X-coordinate therefore remains unaltered. The y and z offsets in the Equatorial frame are denoted by the lower-case letters.
y = Y × cos(o) − Z × sin(o)
z = Y × sin(o) + Z × cos(o)
Compute Greenwich Mean Sidereal Time
Greenwich Mean Sidereal Time is the number of sidereal hours, sidereal minutes and sidereal seconds that the Greenwich Meridian on the Earth is East of the Zero Meridian on the Celestial Sphere at any given instant. The Celestial Sphere's Zero Meridian remains always in the same fixed direction relative to the stars. The Greenwich Meridian always rotates with the Earth. Thus:
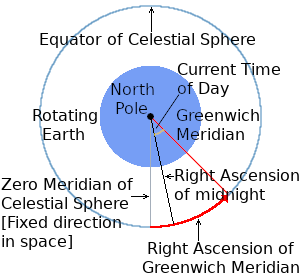 Greenwich Mean Sidereal Time [GMST]
Greenwich Mean Sidereal Time [GMST]
= Right-Ascension of the Greenwich meridian.
= the angle between the zero meridian of the [stationary] Celestial Sphere and the current Right Ascension of the Greenwich Meridian.
Greenwich Mean Sidereal Time [GMST]
= current Right Ascension of midnight
+ current time of day at Greenwich.
The current Right Ascension of midnight
= the current Right Ascension of the Sun
+ π radians.
So current GMST
= RAsun + π + GMT [in radians]
GMT in radians
= 2π × the fraction of the current 24 hour day that has so far elapsed at Greenwich.
= 2π × gms ÷ 86400
'gms' is the number of seconds that has elapsed since last midnight.
There are 86400 seconds in a 24-hour day.
So current GMST
= RAsun + π + 2π × gms ÷ 86400 radians
= RAsun + π × (1 + gms ÷ 43200) radians
For RAsun, in the program code, the Sun's Celestial Longitude 'Ls' is used.
Note that a Sidereal Day is only 23h 56m 04s in terms of normal hours,
minutes and seconds. So Sidereal hours, minutes and seconds are shorter
than normal civil [atomic or Julian] hours, minutes and seconds.
The Mean Sidereal Time in the MOON sub-tab is updated every normal second, like all the other figures. Consequently, every six minutes or so, the Sidereal Clock will jump 2 seconds instead of just one.
Compute Moon's Right-Ascension & Declination
 The Moon's Right-Ascension is its current 'longitude' on the Celestial Sphere. This Celestial Longitude is different from its current Terrestrial [or normal] Longitude because the Earth rotates, while the Celestial Sphere does not. The zero meridian of the Celestial Sphere stays lined up to a fixed direction in space relative to the stars. Of course, if we wish to be pedantic, we may say that the Milky Way galaxy itself is rotating relative to the universe. But its rate of rotation is diminishingly slow, so we regard the stars as stationary.
The Moon's Right-Ascension is its current 'longitude' on the Celestial Sphere. This Celestial Longitude is different from its current Terrestrial [or normal] Longitude because the Earth rotates, while the Celestial Sphere does not. The zero meridian of the Celestial Sphere stays lined up to a fixed direction in space relative to the stars. Of course, if we wish to be pedantic, we may say that the Milky Way galaxy itself is rotating relative to the universe. But its rate of rotation is diminishingly slow, so we regard the stars as stationary.
Right Ascension of the Moon
| Make 'RAm' range from 0 to 2pi because Right Ascension has this range
| | atan2() returns a value between -pi and +pi
| | | y-coordinate of the Moon within the Equatorial Plane
| | | | x-coordinate of the Moon within the Equatorial Plane
| | | | |
RAm = RatAng(atan2(y,X)) Moon's Right Ascension [in radians]
Dm = atan2(z,√(X²+y²)) Moon's Declination [in radians]
| |
| z-coordinate of the Moon, perpendicular to the Equatorial Plane
Declination of the Moon
Compute the Moon's Sub-Point Longitude
The Moon's SUB-POINT is the point on the Earth's surface where the Moon is currently dead overhead. The Moon's sub-point is defined by its terrestrial latitude and longitude. The Moon's sub-point latitude is the same as its Celestial Declination. This is because the earth's axis of rotation is pivoted at the North and South poles of the Celestial Sphere, so that all latitudes on the rotating Earth and on the stationary Celestial Sphere are the same.
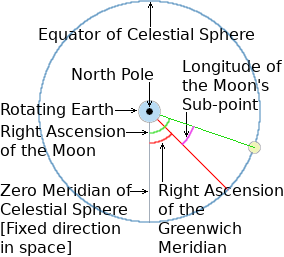 To get the current Terrestrial Longitude of the moon's sub-point from its Right Ascension, it's necessary to take account of the Earth's rotation against the stationary Celestial Sphere. To do this we simply subtract Greenwich Mean Sidereal Time from the moon's Right Ascension. So the current longitude of the Moon's sub-point is its Right Ascension minus the current Greenwich Mean Sidereal Time.
To get the current Terrestrial Longitude of the moon's sub-point from its Right Ascension, it's necessary to take account of the Earth's rotation against the stationary Celestial Sphere. To do this we simply subtract Greenwich Mean Sidereal Time from the moon's Right Ascension. So the current longitude of the Moon's sub-point is its Right Ascension minus the current Greenwich Mean Sidereal Time.
Note that it is not necessary to compute the latitude of the Moon's sub-point because this is exactly the same as the Moon's Declination.
Longitude of Moon's sub-point
| make it into a bipolar angle
| | remove complete turns of 2π
| | | Moon's Right-Ascension
| | | | Greenwich Mean Sidereal Time
| | | | |
Mlng = BipAng(RatAng(RAm − GMST))
Compute the Moon's Azimuth & Elevation
At this stage, I have the Latitude and Longitude of the Moon's sub-point: the point on the Earth's surface at which the Moon is directly overhead. From these, I need to compute the azimuth and angle of elevation of the Moon from the point of view of my Base Station. This is done by the function T7AziEle() in the program. I have the Latitude and Longitude of my Base Station.
Note that, within this program, latitudes & longitudes
and all other angular quantities are given in radians.
The current Latitude of the Moon's sub-point is the same as its Celestial Declination, which is available in global variable D7 in the program. The current Longitude of the Moon's sub-point has already been computed from its Right-Ascension and is available in global variable L7 of the program. The Latitude & Longitude of my Base Station are available in the first record of the Station Data file, which can be readily accessed within the program. However, for test purposes, I created local variables 'Blat' & 'Blng' within T7AziEle(), in which I have written their literal values.
I first need to compute the distance and bearing of the Moon's sub-point from my Base Station. For this I use the function VSGIP(), which embodies the Vincenty Solution to the Geodetic Inverse Problem. It computes distance to a precision of one metre, which is way beyond what is necessary for this computation. But since the VSGIP() function is widely used elsewhere in this program, it is conveniently available. So I make a call to VSGIP() as shown below:
SOLUTION TO THE VINCENTY GEODETIC INVERSE PROBLEM
| latitude of Base Station [in radians]
| | longitude of base station [in radians]
error | | | current latitude of moon's sub-point [in radians]
code | | | | current longitude of moon's sub-point [in radians]
| | | | | | */
e = VSGIP(Blat,Blng,Dm,Mlng);
If successful, VSGIP() returns error code '0' and places the bearing [azimuth] and the great-circle distance of the Moon's sub-point in the global variables FwdAzi & VinDst respectively. If VSGIP() returns a non-zero error code, T7AziEle() displays the appropriate error message and exits because, in this case, there is no point in proceeding further as it will not be possible to compute the Moon's azimuth and elevation angle.
The diagram below shows the geometry required for computing the Moon's angle of elevation from the azimuth and distance. The distance 'd' on the diagram is in the global variable VinDst.
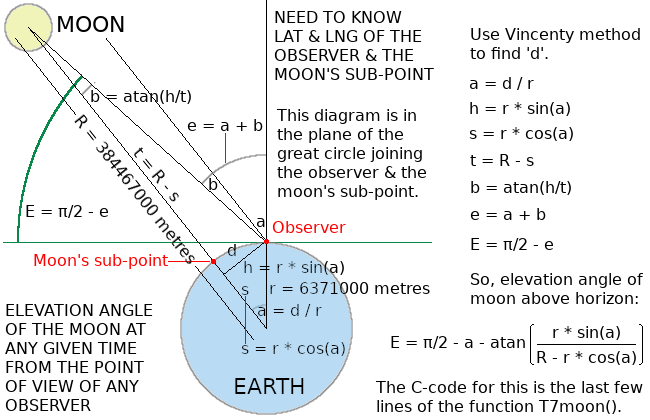
The Earth-Moon distance [distance between the centre of the Earth and the centre of the Moon] has already been computed earlier in T7moon() and placed in the variable 'Rm'. Conveniently, the content of 'Rm' is expressed as the number of Earth-radii. Consequently, the final formula for computing the Moon's elevation angle can be reduced to:
Moon's angle of elevation from the horizontal at the Base Station
| global constant equal to π/2
| | great circle angle: Base Station to Moon's sub-point
| | | returns arc-tangent between -π and +π
| | | | Earth-Moon distance [Earth Radii]
| | | | |
Elev = π/2 − a − atan2(sin(a), Rm − cos(a));
Along with content of the global variable FwdAzi, that of Elev can be passed via an output interface to the Base Station's antenna steering servos to keep the antenna aligned with [pointing at] the Moon all the time the Moon is above the horizon.
Please, if you are in the know, and you come across some gaping error in the above, let me know. Thank you.
The above discourse has been about what I would term the forward problem of computing the bearing and elevation of the Moon from a known location on the Earth's surface at a known date and time. However, there also exists a corresponding inverse problem, namely, to compute the location of an observer on the Earth's surface by observing the Moon's current azimuth and elevation on the current date at the current universal time [UTC/GMT].
I use the rather antiquated terms forward problem and inverse problem in the same sense in which they are traditionally used to describe the two versions of Vincenty's so-called Geodetic Problem mentioned herein.
I think that, due to the nature of the computation, the inverse problem would be more easily solved by iterating the solution to the forward problem, as given above, to progressively reduce the error between the azimuth and elevation as given by the forward solution and the azimuth and elevation as directly observed. This would certainly not over-tax a modern CPU.
This inverse solution would provide a reasonable means of keeping track of one's location on the Earth's surface. As such, it could be integrated into a navigation and flight guidance system. Its accuracy would, of course, vary according to the Moon's current azimuth and elevation relative to the observer [air vehicle]. However, in combination with an inertial dead-reckoning platform, it could provide acceptable accuracy, especially for trans-oceanic stretches.
The independent accuracy of such a navigation and flight guidance system could be progressively improved by constructing an error correction function within a neural network, which could be 'trained' during flights by continually back-propagating the error between the location presented by the Moon Tracker and that provided by a GPS device.
Ground-based radio aids such as VOR/DME [VHF Omni-directional Range stations with Distance Measuring Equipment] and ILS [airport Instrument Landing Systems] could still be used for more accurate navigation over land. These are cheap when compared to global satellite solutions and are always within the direct jurisdictions of their immediate users.
Dependence on any or all of the world's four satellite-based navigation systems — the American GPS, Russian GLONASS, European Union Galileo and Chinese BeiDou — leaves all outsider sovereign states vulnerable to sanctions, which could be applied quickly and at any time simply by changing access encryption keys. Furthermore, it leaves everybody vulnerable to solar flares and coronal mass-ejections.
Thus, in my opinion, it is folly to burn one's bridges by phasing out old technology and failing to exploit less vulnerable natural solutions that do not need expensive artificial infrastructure. But folly prevails. Old technology is forever being discarded at the whim of cost-obsessed bureaucrats who seem to have an addictive propensity for overriding the far better knowledge and advice of engineers.
Conclusion
My greatest take-away from writing this moon tracker program is philosophical. It is well apparent, from the above rat's nest of geometrical formulae and computations, that to us, the motion of the moon with respect to the Earth is excruciatingly complicated. The best we can ever do to try to get a handle of understanding upon what makes the Earth and Moon move the way they do is to try to parse their relative motion in terms of our crude fit-kit of geometrical concepts that is part of the cobbled-together language we call mathematics.
On the other hand, my intuition is that the real [fractal] laws of physics that guide the Earth and the Moon, bit by bit along their respective world-lines, must necessarily be very simple and elegant. The problem is that we have no idea what these laws are. To us, it seems, that they are, and must forever remain, unknown and fundamentally unknowable.
The Earth, Moon, stars, galaxies and the universe do not work according to our mathematics. Our mathematics is just a set of 'try it and see' templates in terms of which we try to express it to ourselves. And that's the way it is. Like it or lump it.
© 30 October 2022 Robert John Morton



 The Moon's True Anomaly [which is designated 'Vm'] is the angle between the line of perigee and the current position of the Moon, as seen from the main focus of the ellipse [the point around which it orbits]. This point is of course the centre of the Earth.
The Moon's True Anomaly [which is designated 'Vm'] is the angle between the line of perigee and the current position of the Moon, as seen from the main focus of the ellipse [the point around which it orbits]. This point is of course the centre of the Earth.



 The adjacent diagram is a 2-D part of the above 3-D diagram. It looks from the Ecliptic North directly on to the Ecliptic Plane. The Moon within the lunar Orbital Plane is tilted upwards towards the viewer. From the lettered sides and angles in the diagram, the Moon's Ecliptic X and Y-coordinates can now be derived as follows.
The adjacent diagram is a 2-D part of the above 3-D diagram. It looks from the Ecliptic North directly on to the Ecliptic Plane. The Moon within the lunar Orbital Plane is tilted upwards towards the viewer. From the lettered sides and angles in the diagram, the Moon's Ecliptic X and Y-coordinates can now be derived as follows.
 These are not the same as terrestrial [normal] latitude and longitude. Terrestrial latitude and longitude are specified with reference to the equatorial plane of the Earth. Ecliptic latitude and longitude are specified with reference to the Ecliptic Plane.
These are not the same as terrestrial [normal] latitude and longitude. Terrestrial latitude and longitude are specified with reference to the equatorial plane of the Earth. Ecliptic latitude and longitude are specified with reference to the Ecliptic Plane.
 Thus, to express the position of the Sun at any given time, we consider its position upon the Ecliptic Sphere. The Ecliptic Sphere is a sphere containing the Earth [I imagine it as a transparent sphere with latitude and longitude lines marked upon its surface such that the axis joining its poles is the Z-axis in our Cartesian [X,Y,Z] coordinates for the Ecliptic Plane. The axis of the Ecliptic Sphere is thus tilted 23·5° from that of the Celestial Sphere. The Earth is at the origin of the Ecliptic Cartesian coordinates. The Ecliptic X-Y Plane slices the Sun and the Earth in half.
Thus, to express the position of the Sun at any given time, we consider its position upon the Ecliptic Sphere. The Ecliptic Sphere is a sphere containing the Earth [I imagine it as a transparent sphere with latitude and longitude lines marked upon its surface such that the axis joining its poles is the Z-axis in our Cartesian [X,Y,Z] coordinates for the Ecliptic Plane. The axis of the Ecliptic Sphere is thus tilted 23·5° from that of the Celestial Sphere. The Earth is at the origin of the Ecliptic Cartesian coordinates. The Ecliptic X-Y Plane slices the Sun and the Earth in half.
 For a positional accuracy better than 2 arc minutes, all the above terms must be added. These are all aspects of the way in which the gravitational influence of the Sun perturbs the position of the Moon, as typified in the adjacent diagram.
For a positional accuracy better than 2 arc minutes, all the above terms must be added. These are all aspects of the way in which the gravitational influence of the Sun perturbs the position of the Moon, as typified in the adjacent diagram.
 Now convert the Moon's Earth-centred X, Y and Z coordinates based on the Ecliptic Plane to Earth-centred X, y, z coordinates based on the Earth's Equatorial Plane, which is the same as the Equatorial Plane of the Celestial Sphere.
Now convert the Moon's Earth-centred X, Y and Z coordinates based on the Ecliptic Plane to Earth-centred X, y, z coordinates based on the Earth's Equatorial Plane, which is the same as the Equatorial Plane of the Celestial Sphere.
 Greenwich Mean Sidereal Time [GMST]
Greenwich Mean Sidereal Time [GMST] The Moon's Right-Ascension is its current 'longitude' on the Celestial Sphere. This Celestial Longitude is different from its current Terrestrial [or normal] Longitude because the Earth rotates, while the Celestial Sphere does not. The zero meridian of the Celestial Sphere stays lined up to a fixed direction in space relative to the stars. Of course, if we wish to be pedantic, we may say that the Milky Way galaxy itself is rotating relative to the universe. But its rate of rotation is diminishingly slow, so we regard the stars as stationary.
The Moon's Right-Ascension is its current 'longitude' on the Celestial Sphere. This Celestial Longitude is different from its current Terrestrial [or normal] Longitude because the Earth rotates, while the Celestial Sphere does not. The zero meridian of the Celestial Sphere stays lined up to a fixed direction in space relative to the stars. Of course, if we wish to be pedantic, we may say that the Milky Way galaxy itself is rotating relative to the universe. But its rate of rotation is diminishingly slow, so we regard the stars as stationary.
 To get the current Terrestrial Longitude of the moon's sub-point from its Right Ascension, it's necessary to take account of the Earth's rotation against the stationary Celestial Sphere. To do this we simply subtract Greenwich Mean Sidereal Time from the moon's Right Ascension. So the current longitude of the Moon's sub-point is its Right Ascension minus the current Greenwich Mean Sidereal Time.
To get the current Terrestrial Longitude of the moon's sub-point from its Right Ascension, it's necessary to take account of the Earth's rotation against the stationary Celestial Sphere. To do this we simply subtract Greenwich Mean Sidereal Time from the moon's Right Ascension. So the current longitude of the Moon's sub-point is its Right Ascension minus the current Greenwich Mean Sidereal Time.
