Neural Networks: The Complete Neuron

An artificial neuron is modelled upon what is thought to be the function of each of the 86 billion biological neurons that make up the essence of the human brain. The biological neuron is almost certainly far more complex than the artificial neuron. Besides, mankind's knowledge and understanding of the full form and function of the biological neuron is still, as yet, somewhat superficial.

An artificial neuron could be constructed as a physical analogue device in which the input weights were rheostats [variable resistors or reverse-biased semiconductor diodes] and with the sigmoid function as a circuit made up of transistors, resistors, capacitors and perhaps even inductors. After all, the biological neuron of the human brain is an analogue device; the whole brain itself — insofar as it may be regarded as a computing device — being strictly an analogue computer: not a digital one.

Although the artificial neuron is an analogue device, the precision and accuracy with which the resistance of a physical rheostat can be set is insufficient for most applications. Vastly greater precision and accuracy can be obtained by simulating the neuron — which is systemically an analogue device — digitally. That is why arti­ficial neural networks are pretty well always implemented as digital simulations.

What follows is my attempt to implement an artificial neuron as a C-function that can be embedded within a full digital simulation of a multi-layer perceptron. It is implemented using 16-bit integers [short integer in 'C'] in anticipation of running it within a multi-layer perceptron programmed into a small electronics package com­prising a 16-bit CPU with the input weights flashed into a ROM chip.

Introduction

The complete neuron comprises the weighted inputs summation function and the sigmoid transfer function as shown below:

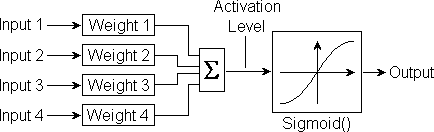
Each input is multiplied by a corresponding weight. All the products are then added together and divided by the number of inputs to yield what is termed the 'acti­vation level'. This is then fed in as input to the Sigmoid() function to produce the neuron's output.

Input Summation

In the document wsum.html and associated source files, we developed the optimum 'C' code for computing a neuron's activation level from its inputs and their corres­ponding weights. This code is shown below:

int i, al, *pi, *pw;
long x, Hi, Lo;
for(pi = I, pw = W, Hi = 0, Lo = 0, i = 0; i < NI; i++) {
  x = (long)*(pi + i) * *(pw + i);
  Lo += x & 0xFFFF;
  Hi += x >> 16;
}
al = ((Hi << 1) + (Lo >> 15)) / NI;

Sigmoid Function

Then, in the document sigmoid.html and associated source files, we developed the optimum 'C' source code for the Sigmoid() function as shown below:

int Sigmoid(int x) {
  int s, y, j;
  if((s = x) < 0) x = -x;
  y = *(SigTab + (j = x >> 5));
  y += ((*(SigTab + j + 1) - y) * (x & 0x1F)) >> 5;
  if(s < 0) y = -y;
  return(y);
}

The Complete neuron

We will now combine these two separately developed and tested pieces of code to form a function to simulate a complete neuron:

int Neuron(int *pi, int *pw, int NI) {
  register i;      // input array index, sigmoid table index
  int a, o, s;     // activation level, neuron output, sign
  long P, Hi, Lo;  // long product, high & low accumulators

  for(Hi = 0, Lo = 0, i = 0; i < NI; i++) {
    P = (long)*(pi + i) * *(pw + i);
    Hi += P >> 16;
    Lo += P & 0xFFFF;
  }
  if((s = (a = ((Hi << 1) + (Lo >> 15)) / NI)) < 0)
    a = -a;
  o = *(SigTab + (i = a >> 5));
  o += ((*(SigTab + i + 1) - o) * (a & 0x1F)) >> 5;
  if(s < 0) o = -o;
  return(o);
}

Note that the names of some of the variables have been changed in order to ration­alise them and help to identify better what they do. The comments adjacent to their declarations explain the new names. We have assigned the index variable 'i' to a register in an attempt to increase speed further. However, nowadays the compiler will assign variables to a resister instead of RAM when appropriate. So it's not really necessary to do this in the code.

Testing

The following exerciser was then written and used to test the completed neuron function:

#include <stdio.h>
#define R  32767
#define RR 65556  // 65534 + 22
#define NI    77  // number of inputs to the current neuron
int AL;           // activation level of the current neuron
short	SigTab[1025];

int I[] = {	 // inputs
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329,
  11376, 13425, 17920, 30226, 28763, 18940, 15329
};

int W[] = {	 // weights
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557,
  12345, 21345, 31245, 16730, 31662, 25460, 13557
};

void SigGen(void) {
  int i;
  for(i = 0; i < 1024; i++)
    SigTab[i] = (double)(
      RR /(1 + exp(-((double)(((long)(i)) << 8))/R))- R
    );
  SigTab[1024] = R;
}

int Neuron(int *pi, int *pw, int ni) {
  register i;      // input array index, sigmoid table index
  int a, o, s;     // activation level, output, sign
  long P, Hi, Lo;  // long product, high & low accumulators

  for(Hi = 0, Lo = 0, i = 0; i < ni; i++) {
    P = (long)*(pi + i) * *(pw + i);
    Hi += P >> 16;
    Lo += P & 0xFFFF;
  }
  if((s = (a = ((Hi << 1) + (Lo >> 15)) / ni)) < 0) a = -a;
  o = *(SigTab + (i = a >> 5));
  o += ((*(SigTab + i + 1) - o) * (a & 0x1F)) >> 5;
  if(s < 0) o = -o;
  AL = a;          // extra line to check activation level
  return(o);
}

main() {
  int OP;
  SigGen();
  OP = Neuron(I, W, NI);
  printf("Activation Level = %6d\n", AL);
  printf("Neuron Output    = %6d\n", OP);
}

The results displayed by this exerciser are as follows:

  Activation Level = 13485
  Neuron Output    = 30439

The neuron function can now be used to build into a complete multi-layer percep­tron. This we do in the document mlpc.htm. A full listing of the multi-layer percep­tron of which this neuron simulation is a part, is in mlp.c.

---

© March 1993 Robert John Morton