Neural Networks: Multi-Layer Perceptron

What It Is

A multi-layer perceptron is one of many different types of neural network. It com­prises a number of active 'neurons' connected together to form a network. The 'strengths' or 'weights' of the links between the neurons is where the functionality of the network resides. Its basic structure is:

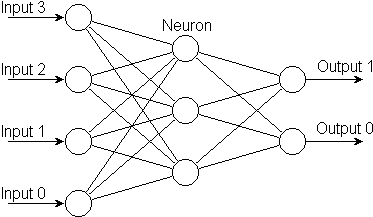
It is usually realised as electronic hardware or as computer software. Its original form though is biological: the whole idea of the neural network stems from studies of the structure and function of the human brain.

What It's For

A neural network's usefulness is in its ability to mimic — or model — the behaviour of real-world phenomena like the weather, the environment, the economy, stock mar­kets, population growth and decay, consumer buying habits, industrial proces­ses, aircraft flight, limb movement.

Being able to model the behaviour of something, a neural network is able subsequ­ently to classify the different aspects of that behaviour, recognise what is going on at the moment, diagnose whether this is correct or faulty, predict what it will do next, and if necessary respond to what it will do next.

Its Strengths

Unlike mathematics, neural networks can faithfully model processes which are non-linear, whose internal workings can only be stated non-explicitly, and which can be only partially observed through many noise-ridden, non-independent variables; which is what in fact all real-world processes are!

How It Works

Instead of being programmed to model a real-world process explicitly, the neural network is trained to model it implicitly. Instead of modelling a real-world process in terms of logical and mathematical functions, the neural network models it as a vast array of 'inter-neural connection weights'.

The Neuron

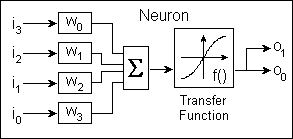
A neuron is an active element which accepts input signals, multiplies each by a cor­responding weight and applies the sum of the weighted inputs to a transfer func­tion to produce an output signal:

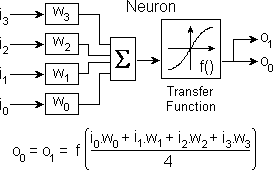
A neuron's transfer function is usually a sigmoid function as shown above.

The design, testing and optimising of 'C' code for summing the weighted inputs is documented in wsum.html. The compilable 'C' code embedded in an exerciser for benchmarking and time trials are in wsum1.c, wsum2.c and wsum3.c. These execu­table programs are in wsum1.exe, wsum2.exe and wsum3.exe. Similar treatment of the sigmoid function is in sigmoid.html, sigmoid.c and sigmoid.exe. The 2 pieces of code are then combined and tested as a complete neuron in neuron.html, neuron.c and neuron.exe.

NOTE: The above executables were compiled for Microsoft Windows 95 circa. 1997. To run them on Linux today [2024] the source code will need to be edited before compiling with a Linux-compatible compiler e.g. gcc.

Scaling

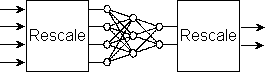
Signals within the network are scaled to a range and precision which suits the hard­ware or software platform on which the network is implemented. For example, a software implementation may run at its fastest when it is based on 16-bit integers. In this case, signals from the outside world would be rescaled to the range +32767 to −32767. Conversely, outputs from the network would be rescaled back to the range and precision expected by the outside world:

Layers

The vertical columns of neurons as shown in the following diagram are known as layers. A layer receives signals from the one before it and passes its outputs to the one which follows.

All networks have an input layer and an output layer. A network may also have hidden layers whose neurons have no direct connections to the outside world.

Internal Structure

Below is a typical neural network showing the internal structure of a neuron:

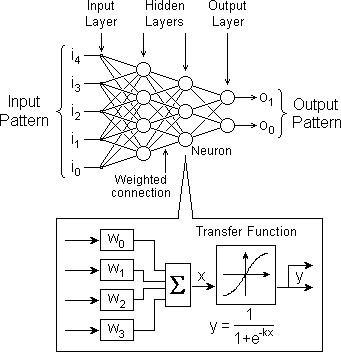
We will implement this network as a 'C' function.

Implementation in 'C'

Data Structure

The data structure required for this network comprises a one-dimensional array to hold the output signals from each layer plus a two-dimensional array to hold the weights of the connections between each pair of layers:

To take advantage of the pointer arithmetic capabilities of the 'C' language we must organise the data arrays slightly differently. Firstly we must make all the layer out­puts accessible via a single pointer array L[ ] as follows:

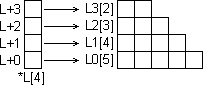
The array L0[ ] containing the network's inputs from the outside world, is in fact declared within the object which produces the inputs. Its declaration is therefore external to the source file with which we are concerned here. It is probably not even called L0[ ]. But we do not need to know what it is called. Our multi-layer per­ceptron function is told where to find its input by way of a pointer po which is pas­sed to it as an input argument as follows:

  short *mlp(short *po) {

  }

We do not therefore declare L0[ ]. Notice that our multi-layer perceptron function also returns a pointer to the external function that called it. This is to let the caller know where to find the network's outputs. This arrangement allows us to develop our multi-layer perceptron function (plus later its learning algorithm) as an indep­endent object which can be linked by an object linker to different 'outside world' interface handlers as follows:

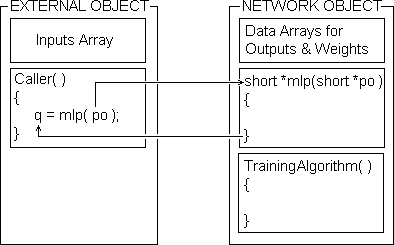
We must set up a similar data structure for each of the sets of inter-layer connec­tion weights.

Because each weights array is two-dimensional, we need an extra level of indir­ec­tion. Instead of being an array of pointers to integers like L[ ], W[ ] must be declar­ed as an array of pointers to pointers to integers. All the weights arrays relating to a given layer of the network must be accessed through an intervening level of arrays of pointers to integers as follows:

The first element of W[ ], namely W[0], does not point to anything. This is to align the indexing with L[ ] which also does not use its first element for the reasons al­ready given.

Declarations

The formal declarations of the layer outputs data arrays will therefore be:

//Layer output arrays
int L1[4], L2[3], L3[2], *L[4] = {NULL, L1, L2, L3};

The NULL element is there because L[0] does not point to anything as discussed above.

We need to split the two-dimensional inter-layer weightings arrays into sets of one-dimensional integer arrays as follows:

int W10[5], W11[5], W12[5], W13[5],//Layer 0-1 connection weights
    W20[4], W21[4], W22[4],        //Layer 1-2 connection weights
    W30[3], W31[3];                //Layer 2-3 connection weights

Each of these arrays has a dimension equal to the number of inputs to each neuron in the layer concerned.

We must declare an array of pointers-to-integers for each set of arrays:

int *W1[4] = {W10, W11, W12, W13},	
    *W2[3] = {W20, W21, W22},
    *W3[2] = {W30, W31};

Each of these arrays has a dimension equal to the number of neurons in the layer concerned.

Finally, we need an array of pointers-to-pointers-to-integers to point to the two above arrays of pointers. This will have a dimension equal to the total number of layers in the network as follows:

int **W[4] = {NULL, W1, W2, W3};

Although this more complicated approach needs extra storage for the pointers, it has two great advantages over the two-dimensional arrays:

1. It only takes 2 indirect addressing operations to access an element in either of the two sets of arrays. Separate program statements would be needed to access the two 2-D arrays and these would invoke a time-consuming mult­iply and add operation.

2. Any element in either array is accessible via a single generalised program statement thus allowing the weighting calculations for the whole network to be performed from within a single program loop.

Generalisation

We can make the data declarations a little easier to adapt to different sizes of net­work by defining symbolically the number of layers, the number of neurons in each layer, and the number of inputs:

#defineNL  4  //total number of network layers
#defineNAL 3  //number of active layers in the network 
#defineN0  5  //number of inputs (ie outputs from Layer 0)
#defineN1  4  //number of neurons in Layer 1
#defineN2  3  //number of neurons in Layer 2
#defineN3  2  //number of neurons in Layer 3

We may then make the data declarations slightly more generalised:

int N[] = {N0, N1, N2, N3};           //Neurons per layer
short
  L1[N1], L2[N2], L3[N3],             //Layer output arrays
  *L[] = {NULL, L1, L2, L3},          //Access to layer outputs 
  W10[N0], W11[N0], W12[N0], W13[N0], //Layer 1 input weights
  W20[N1], W21[N1], W22[N1],          //Layer 2 input weights
  W30[N2], W31[N2],                   //Layer 3 input weights
  *W1[] = {W10, W11, W12, W13},       //Access to L1 weights
  *W2[] = {W20, W21, W22},            //Access to L2 weights
  *W3[] = {W30, W31},                 //Access to L3 weights
  **W[] = {NULL, W1, W2, W3};         //Access to all weights

The arrays relating to output and weight data are now declared as 'short'. This is to ensure that these will be 16-bit quantities even on a 32-bit CPU. These are declared and initialised outside the function because they will be used directly by another function which we shall discuss later. Note that we need to declare extra arrays if we wish to enlarge the network.

The Skeletal Function

To create the complete multi-layer perceptron function we proceed as follows. Only the array declarations need be altered to change the size and shape of the net­work.

#define NL  4  //number of network layers 
#define NAL 3  //number of active network layers 
#define N0  5  //number of network inputs in Layer 0
#define N1  4  //number of active neurons in Layer 1
#define N2  3  //number of active neurons in Layer 2
#define N3  2  //number of active neurons in Layer 3
short
  N[] = {N0, N1, N2, N3},             //Neurons per layer
  L1[N1], L2[N2], L3[N3],             //Layer output arrays
  *L[] = {NULL, L1, L2, L3},          //Access to layer outputs 
  W10[N0], W11[N0], W12[N0], W13[N0], //Layer 1 input weights
  W20[N1], W21[N1], W22[N1],          //Layer 2 input weights
  W30[N1], W31[N1],                   //Layer 3 input weights
  *W1[] = {W10, W11, W12, W13},       //Access to L1 weights
  *W2[] = {W20, W21, W22},            //Access to L2 weights
  *W3[] = {W30, W31},                 //Access to L3 weights
  **W[] = {NULL, W1, W2, W3},         //Access to all weights
  SigTab[1025];                       //Sigmoid function look-up table

void mlp(short *po) {          //ptr to initial inputs array
  int nl;                      //current network layer
  for(nl = 1; nl < NL; nl++){  //for each layer of network
    int nn, NN = *(N +	nl);   //neurons in this layer
    short *pi = po,            //ptr to layer's inputs array
    **ppw = *(W + nl);         //ptr to neurone's input weights
    po = *(L + nl);            //ptr to neurone's output element
    for(nn = 0; nn < NN; nn++) //for each neuron in the layer
    {

    }
  }
}

Full research and development details of the code for the neuron are dealt with in the document files wsum.html and sigmoid.html.

The constants definitions and array declarations external to the function are as de­scribed previously with the addition of an array called SigTab[ ] which holds a look-up table for the neurone's sigmoid transfer function.

The Layers Loop

The multi-layer perceptron is what is termed a feed-forward network. The output values for one layer must all be computed before it is possible to compute any output values for the next layer. The first loop therefore deals in layers starting from the input layer and working through to the output layer. The index which holds the number of the layer currently being dealt with is the integer nl. Therefore, inside the braces of the Layer Loop's for statement:

  for (nl = 1; nl < NL; nl++) {

  }

we are dealing with a single layer of the neural network. Notice that nl ranges from 1 to NL − 1 and not 0 to NL − 1. There are no neurons in Layer Zero. For indexing convenience, we regard the inputs from the outside world as outputs from Layer Zero.

Input & Output Pointers

The pointer po received from the calling function as an input argument is the start address of an array declared externally which contains the input.

When the array L[ ] was declared, the first element was reserved by declaring it NULL. This was to save the first element of L[ ] for the start address of the extern­ally-declared inputs array. The pointer in L[0] thus would point at the externally-declared input array as shown below:

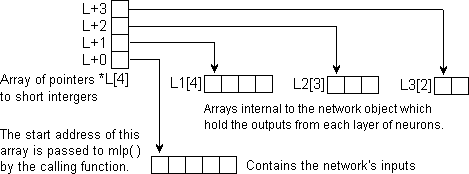
This would be achieved by the statement L[0] = po. However, we do not actually need to do this. If we adopt the input argument po as the pointer to each layer's outputs array in turn from Layer 1 through to the last layer, we do not need to refer to L[0] at all as we shall see later.

Before we can update the outputs from the neurons in a given layer nl, we must first determine the start address of the array of inputs to the neurons in that layer, and the start address of the array of outputs from that layer. These start addresses (which we assign to the pointer variables pi and po respectively) are determined as follows:

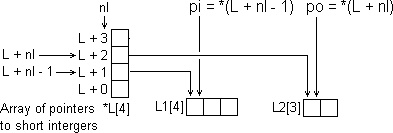
But since on entry to the function, po starts off holding the start address of the inputs to the network (which we regard as the outputs from our Layer Zero), we can simply copy this initial address into the pointer variable pi and then put into po the start address of the layer's outputs array:

  short *pi = po;  // Make last time's output layer this time's input layer
  po = *(L + nl);  // then set po to point to this time's output layer

We put these statements immediately inside the layers loop so that for each new pass, last time's outputs become this time's inputs.

Input Weights

Each neuron has its own separate weight value for each input it receives. This means that for each input to a layer there is a corresponding set of weights. So to access weights, we need an extra level of indirection.

Before we can enter the loop that processes each neuron in turn, we need to set a pointer, pw to point to the start address of the array of weights for the inputs to Neuron Nº 0 of Layer nl using a statement:

  short **ppw = *(W + nl);

Notice that ppw must be declared as a pointer to a pointer to a short integer.

Going on a stage further, the start address of the array of weights for any given neuron nn, is given by:

  short *pw = *(ppw + nn);

Since we have reduced the number of levels of indirection by one, pw is only de­clared as a pointer to a short integer.

How these pointers relate to the whole structure of the weights arrays can be seen from the following diagram:

The Neuron Loop

Within each layer of the network is a prescribed number of neurons. This number is decided by the designers for a particular network application.

The number of neurons in each layer is held in the array N[]. The number of neur­ons in Layer Nº nl is therefore N[nl]. We can therefore declare the number of neur­ons in the layer that we are dealing with at the moment as NN = *(N + nl). We indicate a particular individual neuron within Layer nl by its neuron number nn. Thus nn runs from 0 to NN within Layer nl.

Both of mlp()'s for() loops are controlled by integer index variables, nl and nn. The pointer variables pi and pw could be used. These would be incremented each pass of the outer and inner loops respectively from the start address (lower bound) of the array concerned until they reached a value just beyond the end (upper bound) of the array.

This method of loop control saves the need for integer index variables.

But the loop test address will go beyond the end of the array concerned and this could lie outside the application's permitted memory bounds. If referenced, even if never read from or written to, it could precipitate a memory protection violation error at run-time in some operating systems.

Also, ironically, it has been found under test that to access a value such as a weight using the construct *(pw + ni) with ni++ in the for() statement is faster than using the simpler construct *pw++ on its own.

The Neuron Sub-Function

The development and validation of the 'C' code for our MLP neuron is fully docu­mented in wsum.html, sigmoid.html and neuron.html. The final code presented as a complete 'C' function is shown below:

int Neuron(int *pi, int *pw, int NI) {
  int ni,                 //input array index
      a,                  //activation level
      o,                  //neuron output
      s;                  //sign
  long Hi, Lo;            //high & low accumulators
  for (Hi = 0, Lo = 0, ni = 0; ni < NI; i++) {
    long P = (long)*(pi + ni) * *(pw + ni);
    Hi += P >> 16; Lo += P & 0xFFFF;
  }
  if((s = (a = ((Hi << 1) + (Lo >> 15)) / NI)) < 0) a = -a;
  o = *(SigTab + (ni = a >> 5));
  o += ((*(SigTab + ni + 1) - o) * (a & 0x1F)) >> 5;
  if (s < 0) o = -o;
  return(o);
}

We could simply call this function from within the neuron loop, but since it is small and in a very speed-critical position, we will insert it as in-line code. To do this, we must add the emphasised statements below:

  int ni,                 //input array index
      a,                  //activation level
      o,                  //neuron output
      s;                  //sign
      NI = *(N - 1 + nl); //number of inputs to this neuron
  short *pw = *(ppw + nn);//ptr to neurone's first input weight
  long Hi, Lo;            //high & low accumulators
  for (Hi = 0, Lo = 0, ni = 0; ni < NI; i++) {
    long P = (long)*(pi + ni) * *(pw + ni);
    Hi += P >> 16; Lo += P & 0xFFFF;
  }
  if((s = (a = ((Hi << 1) + (Lo >> 15)) / NI)) < 0) a = -a;
  o = *(SigTab + (ni = a >> 5));
  o += ((*(SigTab + ni + 1) - o) * (a & 0x1F)) >> 5;
  if (s < 0) o = -o;
  *po = o;                //store this neurone's output value

The number of inputs to a neuron in layer nl is the same as the number of outputs from the layer nl − 1 which is found in element (nl − 1) of array N[ ]. In pointer notation this is given by NI = *(N + nl) as shown. Pointer, pw, to the current neur­one's first weight was explained in the previous diagram. Finally, we place the neur­al output, o in the output array element *po.

The Complete 'C' Function

#defineNL  4  //number of network layers 
#defineNAL 3  //number of active network layers 
#defineN0  5  //number of network inputs in Layer 0
#defineN1  4  //number of active neurons in Layer 1
#defineN2  3  //number of active neurons in Layer 2
#defineN3  2  //number of active neurons in Layer 3
short	
  N[] = {N0, N1, N2, N3},             //Neurons per layer
  L1[N1], L2[N2], L3[N3],             //Layer output arrays
  *L[] = {NULL, L1, L2, L3},          //Access to layer outputs 
  W10[N0], W11[N0], W12[N0], W13[N0], //Layer 1 input weights
  W20[N1], W21[N1], W22[N1],          //Layer 2 input weights
  W30[N1], W31[N1],                   //Layer 3 input weights
  *W1[] = {W10, W11, W12, W13},       //Access to L1 weights
  *W2[] = {W20, W21, W22},            //Access to L2 weights
  *W3[] = {W30, W31},                 //Access to L3 weights
  **W[] = {NULL, W1, W2, W3},         //Access to all weights
  SigTab[1025];                //Sigmoid function look-up table

void mlp(short *po) {   //ptr to initial inputs array
  int nl;               //index number of current network layer

  for(nl = 1; nl < NL; nl++) { //for each layer of network
    int nn, NN = *(N + nl);    //neurons in this layer
    short *pi = po,            //ptr to layer's inputs array
    **ppw = *(W + nl);         //ptr to neurone's input weights
    po = *(L + nl);            //ptr to neurone's output element

    /*For each neuron in this layer, declare variables 
      for the neuron number ni, its activation level a,
      its output o, the sign of its output s, its number 
      of inputs NI, pointer to its first input weight pw,
      plus two 32-bit variables to form the Hi and Lo 
      portions of a 48-bit accumulator for multiplying. */

    for(nn = 0; nn < NN; nn++) {
      int ni, a, o, s, NI = *(N - 1 + nl);
      short *pw = *(ppw + nn); 
      long Hi = 0, Lo = 0;

      /*for each input to neuron... (See the narrative on the 
        weighted input summation and sigmoid functions.) */

      for(ni = 0; ni < NI; ni++) {
        long P = (long)*(pi + ni) * *(pw + ni);
        Hi += P >> 16; Lo += P & 0xFFFF;
      }
      if((s = (a = ((Hi << 1) + (Lo >> 15)) / NI)) < 0) a = -a;
      o = *(SigTab + (ni = a >> 5));
      o += ((*(SigTab + ni + 1) - o) * (a & 0x1F)) >> 5;
      if (s < 0) o = -o;
      *po = o;   //store neurone's output in layer output array
    }
  }
}

Wish List

Need a file I/O function to handle the examples file for learning. Need a function to display the weights arrays graphically so that we can watch the network learn.

---

© December 1997 Robert John Morton