This Moving Map was built as a small demonstrator for the EBS Nomad Project. The function MapBox() creates a square map window centred on the aircraft. Within this map window ShowNode() displays solid circles. These represent way points such as geographical features or cities. The scale of the moving map can be varied over a wide range. When the scale covers a very wide area, the function NodeTilt() is called to transform the solid circles into ellipses. This mimics the effect of their angling due to the curvature of the Earth.
The way-points move on the map as the aircraft travels. The names and coordinates of all the way points are kept in a file called WayPts.DAT. After calling MapIni() to initialise the map display, main() cycles endlessly through WayPts.DAT calling RandB() to compute (using full spherical geometry) the distance and bearing of each way point in turn from the aircraft. These are then converted by RBtoXY() to logical screen co-ordinates. Its circle (or ellipse) is then re-displayed in the map window. It also calls ShowData() which displays the aircraft's current co-ordinates, heading, height and speed. To do this it calls RadKm() and RadDeg() to convert the Earth radians used in the computations to kilometres and degrees for display. Details about the next way-point are also shown.
This test-bed program flies the aircraft at 1000km/hr from Stansted to Ringway. Its motion is effected by GndTrk(). This contains a radial intercept function which brings the aircraft on to Ringway's approach radial from its take-off heading at Stansted.
From this test-bed project, I developed a waypoint radial capture function to be used in navigation applications.
#include <graph.h>
#include <math.h>
#include <malloc.h>
/* Define ERESCOLOR raster's true aspect ratio on an IBM 8513
VGA screen: */ #define ASPECTRATIO .6834532737
/* Define the number of kilometres equivalent to one Great
Circle radian: */ #define KMPERRADIAN 6366.197723857773
/* Define the number of radians/second equivalent to one
kilometre/hour */ #define KMH_RADS .4363323129861111E-7
/* Define the number of degrees/minute equivalent to one
radian/second: */ #define RADS_DEGM 3437.74677
#define X_DIAM 100 // Diameter of scale square on map in Xpixels
#define X_SQUR 200 // Diameter of scale square on map in Xpixels
extern char *RadDeg(double c);
double Y_DIAM = X_DIAM * ASPECTRATIO,
Y_SQUR = X_SQUR * ASPECTRATIO;
extern double // All measured in radians
ObsLat, ObsLng, // Observer's lat/long
DstLat, DstLng, // Destination lat/long
ObsHdg, ObsVel, // Observer's direction and velocity
Range, // Distance of feature (eg city) from Observer
Bearing, // Bearing of the feature as viewed by Observer
ObsRot, // Observer's rate of rotation (radians/sec)
ReqHdg, // Commanded heading to bring vehicle on to Radial
Radial; // Destination radial on which observer must travel
Set up an area of memory to hold:
- the graphics image of the movable solid circle which represents a map feature (such as a city) and
- the movable graphics images of each capital letter and certain other ASCII characters.
If compiling with CL, a static array char far Graph[2156] can be used. However, QC does not support far static data, so we must use malloc() to allocate an area of memory dynamically.
char
far *GraphBuf, // Pointer to `city blob' image
far *Letters; // Pointer to letter images
Display the basic map screen on the currently-active page.
MapBox() {
_settextcolor(6); _settextposition(1,1);
_outtext("EBS VEHICLE NAVIGATION SYSTEM");
_moveto(-X_DIAM, Y_SQUR + 17);
_lineto( X_DIAM, Y_SQUR + 17);
_settextposition(24, 53); _outtext("100km");
_settextcolor(3);
_settextposition(4,1); _outtext("NEXT WAY POINT");
_settextposition(5,1); _outtext("LATITUDE");
_settextposition(6,1); _outtext("LONGITUDE");
_settextposition(7,1); _outtext("DISTANCE TO GO km");
_settextposition(8,1); _outtext("INBOUND RADIAL");
_settextposition(10,1); _outtext("VEHICLE");
_settextposition(11,1); _outtext("LATITUDE");
_settextposition(12,1); _outtext("LONGITUDE");
_settextposition(13,1); _outtext("HEADING");
_settextposition(14,1); _outtext("SPEED km/hr");
_settextposition(16,1); _outtext("REQ'D HEADING");
_settextposition(17,1); _outtext("RATE OF TURN ø/min");
}
Set up the graphics images necessary for displaying annotated map features (such as cities) within the map window:
MapIni() {
int a, ox, oy; // Logical origin of Map Window
char far *Letter;
struct videoconfig config; // Defines CGA, EGA, VGA etc.
_setvideomode(_ERESCOLOR); // Mode to 16-colour 640 x 350
_setactivepage(1); // Set Page 1 active while
_setvisualpage(0); // displaying Page 0
/*Allocate 2156 bytes of buffer and put its start address
in the far char pointer 'GraphBuf'. 76 bytes are for the
city blob, the rest is for the captured text characters
at 40 bytes per character.*/
GraphBuf = (char far *)malloc((unsigned int) 2156);
Letters = GraphBuf + 76;
/*Form the blob to represent a city and store its image in the graphics
image buffer pointed to by `graphbuf' this image occupies first 76 bytes
of the buffer.*/
_setcolor(9);
_moveto(4,0); _lineto( 8,0);
_moveto(2,1); _lineto(10,1);
_moveto(1,2); _lineto(11,2);
_moveto(0,3); _lineto(12,3);
_moveto(0,4); _lineto(12,4);
_moveto(0,5); _lineto(12,5);
_moveto(1,6); _lineto(11,6);
_moveto(2,7); _lineto(10,7);
_moveto(4,8); _lineto( 8,8);
_getimage(0,0,12,8,GraphBuf);
/*Display the alphabet on the screen, then capture each letter as a graphics
image and store it in the graphics buffer from byte 76 onwards. The image
of each letter occupies 40 bytes of buffer.*/
_settextcolor(7);
_settextposition(1,1);
_outtext(
"'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ"
);
for(a = 0, Letter = Letters; a < 416; a += 8, Letter += 40)
_getimage(0 + a, 2, 7 + a, 10, Letter);
_clearscreen(_GCLEARSCREEN);
/*Set the logical co-ordinates origin to the centre of the map display
window. (Effective for both video pages.) */
_getvideoconfig(&config);
ox = config.numxpixels / 2 + 115;
oy = config.numypixels / 2;
_setlogorg(ox, oy);
//Set up the main screen format on both video pages 0 and 1
MapBox(); _setactivepage(0); _setvisualpage(1); MapBox();
_settextcolor(7);
//Limit graphics area to window. Effective on BOTH video pages.
_setcliprgn(
ox - X_SQUR, oy - Y_SQUR + 1, ox + X_SQUR, oy + Y_SQUR
);
}
Compute X,Y screen co-ordinates from the range & bearing in radians. Assumes logical co-ordinates are at centre of 640 by 350 pixel VGA screen. If scale <= 1 nautical mile per pixel, curvature of screen ÷ that of the Earth so the actual range on the Earth's surface is used to compute the x,y screen co-ordinates. If scale > 1 nautical mile per pixel the surface range is projected onto the Earth's tangential plane at the observer point (centre-screen) before x,y are computed. Returns zero co-ordinates if the 'observed' is out of screen range.
int *RBtoXY(float s) {
static int a[2]; // array for screen co-ordinates
double x, y, z,
d = Range * KMPERRADIAN, // in km (20,000/pi km/radian)
b = Bearing - ObsHdg; // bearing in radians + heading
if(s > 2) d *= sin(Range); /* If scale > 2km/pixel, project range
onto tangential plane. */
if(s > 0) d /= (z = s); // Re-scale from km to pixels
x = d * sin(b); // screen x-pixel
y = d * cos(b); // screen y-pixel
if(x > 0) x += .5; else x -= .5; // Do appropriate negative
if(y > 0) y += .5; else y -= .5; // or positive rounding.
if(x > 185 || x < -185 || // safe screen x-range limit
y > 185 || y < -185) { // safe screen y-range limit
x = 1000; y = 1000; // set zero co-ordinates
} // if target is off screen
/*Store the x-displacement as is, and the y-displacement scaled to the MRES
screen aspect ratio. Then return the pointer to the co-ordinates array.*/
*a = x; *(a + 1) = -y * ASPECTRATIO; return(a);
}
Display a city or a waypoint on the Earth's surface as a small annotated circle or ellipse.
ShowNode (
int *q, // Pointer to city's SCREEN co-ordinates array.
char *n // Pointer to city's name string.
) {
int x = *q, y = *(q + 1), // x-y co-ordinates of city
i, // Letter Nº within City Name
l, // Nº of characters in annotation
m; // repeat of l
_putimage(x-6, y-4, GraphBuf, _GPSET); // Display the city
for(l = 0; *n != ' '; l++, n++); // Find length of its name
n -= l;
//PUT CITY'S NAME LEFT, RIGHT, ABOVE, BELOW THE CITY ITSELF
m = l;
switch(*(n + 15)) {
case 'L': x -= (8 + (m <<= 3)); break; // annotate left
case 'R': x += 10; break; // annotate right
case 'A': x -= (m <<= 2); y -= 13; break; // annotate above
case 'B': x -= (m <<= 2); y += 13; // annotate below
}
/*Display the name of the city by displaying in sequence at the city's
screen co-ordinates the letters of its name as graphics images of the
normal text letters.*/
for(i = 0; i < l; i++, x += 8) // For each letter of the name
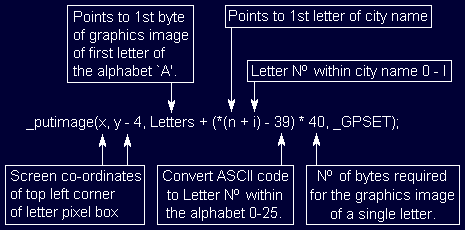
_putimage(x, y - 4, Letters + (*(n + i) - 39) * 40, _GPSET);
}
Converts a 'double' in Earth-radians or Earth-radians/second to a 5-byte string showing km or km/hr respectively:
char *RadKm(double d, int e) {
int a, b, c, latch = 0, x = ' ';
char *s = " ", *t = s, *o = "OVFLOW";
if(e == 0) d *= KMPERRADIAN;
else if (e == 1) d /= KMH_RADS;
else if (e == 2) d *= RADS_DEGM;
if(d > 32767 || d < -32767) s = o;
else {
b = d;
if(b < 0) { b = -b; x = '-'; }
for(a = 10000; a > 1; a /= 10, t++) {
for(c = 0; b >= a; b -= a, c++);
if(!latch) { // If latch not yet set,
if(c == 0) // if digit value is zero
*t = ' '; // store a leading space
else { // else if first non-zero digit
latch = 1; // set the latch
*t++ = x; // store the sign
*t = c + 48; // store character, including zeros.
}
} else *t = c + 48; // store character, including zeros.
}
if(!latch) *t++ = x; // store the sign
*t = b + 48;
}
return(s);
}
Updates the text-based navigation data on the screen:
ShowData() {
static int pg;
_setcolor(7); // Set to display in white
_moveto(-X_DIAM,-Y_DIAM); // Re-display the inner square
_lineto(X_DIAM,-Y_DIAM); _lineto(X_DIAM,Y_DIAM);
_lineto(-X_DIAM,Y_DIAM); _lineto(-X_DIAM,-Y_DIAM);
//Re-display the cross-hairs at the centre of the map window
_moveto(-14, 0); _lineto( 14, 0);
_moveto( 0, 10); _lineto( 0,-10);
_settextposition( 5,16); _outtext(RadDeg(DstLat));
_settextposition( 6,16); _outtext(RadDeg(DstLng));
_settextposition( 7,16); _outtext(RadKm(Range,0));
_settextposition( 8,16); _outtext(RadDeg(Radial));
_settextposition(11,16); _outtext(RadDeg(ObsLat));
_settextposition(12,16); _outtext(RadDeg(ObsLng));
_settextposition(13,16); _outtext(RadDeg(ObsHdg));
_settextposition(14,16); _outtext(RadKm(ObsVel,1));
_settextposition(16,16); _outtext(RadDeg(ReqHdg));
_settextposition(17,16); _outtext(RadKm(ObsRot,2));
_setvisualpage(pg); // Display completed graphics page
pg ^= 1; // Flip video page: 0 -> 1; 1 -> 0
_setactivepage(pg); // Set old display page for updating
_setcolor(8);
_rectangle(_GFILLINTERIOR, -X_SQUR, -Y_SQUR, X_SQUR, Y_SQUR);
}
Displays a feature on the Earth's surface as a small filled circle which is tilted if necessary so that it appears as an ellipse whose major to minor axis ratio shows the effect of the Earth's curvature according to the feature's displacement from the point of observation at the centre of the screen.
ShowNode (
double *p, // Pointers to feature's EARTH &
int *q, // SCREEN co-ordinates arrays.
char *n, // Pointer to annotation name.
int c // Display colour (can be black)
) {
double
tilt = *(p + 2), // tilt of feature on the Earth
CosPsi = *(p + 3), // Cosine of bearing
TanPsi = *(p + 4), // Bearing of feature from centre
t, // Angle in generation of ellipse
z, w; // Working variables
int
x = *(q + 1), // x-position of observed object
y = *(q + 2), // y-position of observed object
i = 1, // `first time through' switch
r = 7, // major axis radius of ellipse
u, // Ellipse-gen X-displacement
v, // Ellipse-gen Y-displacement
l = 0, // Nº of characters in annotation
c = *(n + 14) - 48; // Display colour
If(CosPsi != 0) { // To prevent division by zero
if(s) c = 0; // set colour black if re-display
_setcolor(c);
//Take t round in a full circle in 0.1 radian steps
for(t = 6.5; t > 0; t -= .1) {
w = tilt * r * cos(t);
z = CosPsi * (r * sin(t) - w * TanPsi);
v = w / CosPsi + z * TanPsi;
u = z;
if(i == 0) // If not first pass of loop,
_lineto( x + u, y + v ); // draw line to next valid point
else {
i = 0; // else clear `first pass' flag
_moveto( x + u, y + v ); // and set position to start of
} // ellipse locus.
}
_floodfill(x, y, c); // Fill in the ellipse
while(*n != ' ') {l++; n++;} // Find length of city name
n -= l;
/*Annotate the ellipse with the name of the city or way point it repres-
ents. Place the name at the left, right, above or below the ellipse as
appropriate.*/
switch(*(n + 15)) {
case 'L': x -= (7 + l * 7); break; // left
case 'R': x += 10; break; // right
case 'A': x -= (l * 7 / 2); y -= 13; break; // above
case 'B': x -= (l * 7 / 2); y += 13; // below
} annotate( x, y, l, n );
}
}
Please note that this function is not used in the current demonstrator.
I had to find a way to represent the Earth in terms of numeric data. This was long before Geographic Information Systems and databases became generally available. The purpose at hand did not require a high degree of resolution or detail. The marking of coastlines was unnecessary. I decided to build my geographic data model of the Earth entirely of way points placed on a true sphere. Nothing more would be gained by representing the Earth as a distorted ellipsoid with land relief and oceanic bulges.
I conveniently found a world-wide listing of 11,000 cities and major geographical features together with their co-ordinates in the back of my daughter's school atlas. As I was going to use the data for experimental purposes only and not for commercial gain I decided that it would be permissible to use it. Entering this list was a long and boring job. I entered the names and co-ordinates 10 at a time in odd sessions over a long period. This is the Earth model used as the basis for this Moving Map project.
This file contains all the C code for my demo flight system which flies an ideal aircraft from Stansted (London) to Ringway (Manchester). It displays point features (or nodes) on the Earth's surface from their latitudes and longitudes. The screen represents a spheroidal section of the earth's surface rather than a `projected' map. Unlike a map projection, therefore, all the variables; range, bearing, shape and area are correct. Note: the RandB() function is in the file RandB.C.
#include <graph.h>
#include <math.h>
#include <stdio.h>
extern double DegRad(char *p, int l); // in RandB.C
extern char *RadDeg(double c); // in RandB.C
extern double RandB(double RefLat, double RefLng, int Swap);
extern GndTrk(); // in file GndTrk.C
extern int *RBtoXY(float s);
extern int MapInit();
extern ShowNode(int *q, char *n); // in file NodeTilt.C
char *RadKm(double d, int e);
#define Pi 3.1415926535
#define TwoPi 6.283185307
#define CITIES 24 // Nº of cities (sizeof city array)
#define CITYRL 81 // 80 data bytes + \0 terminator
#define OBSERVER 5 // City Nº of observer
#define LATBYTE 17 // Byte Nº of lat within city record
#define LNGBYTE 28 // Byte Nº of lng within city record
#define SCALE .5 // Map scale in km per X-pixel
#define VEH_SPEED 1000 // Vehicle speed in Km/hr
#define WINDOW_WIDTH 200 // ½-width of map window (pixels)
#define KMH_RADS .4363323129861111E-7 // km/hr to rad/sec
char city[CITYRL]; // Holds data relating to one city
// THE FOLLOWING VARIABLES ARE SCALED IN EARTH-RADIANS
double
ObsLat, // Observer's (or vehicle's) current latitude
ObsLng, // Observer's (or vehicle's) current longitude
RefLat, // Reference-point's (or city's) latitude
RefLng, // Reference-point's (or city's) longitude
MaxRng, // Cosine of maximum range we are interested in
ObsVel, // Observer's current velocity (radians/sec)
ObsHdg, // Observer's current heading (radians)
ObsRot, // Observer's rate of turn (radians/sec)
DstLat, // Latitude of destination (or way point)
DstLng, // Longitude of destination (or way point)
Range, // Range of Reference object from observer
Bearing, // Bearing of Reference object from observer
CosRng, // Cosine of the range
CosBrg, // Cosine of the bearing
TanBrg, // Tangent of the bearing
ReqHdg, // Required Heading to come smoothly on to the radial
Radial; // Radial which vehicle must endeavour to follow
The following is the basis for the dLat test which determines the approximate in-window range before RandB() is used. The size of a latitude-radian is fixed at 40,000 / 2pi kilometres. The size of a Longitude-radian varies with latitude.
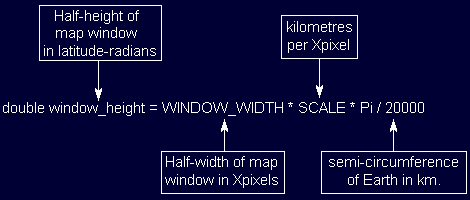
double window_height = WINDOW_WIDTH * SCALE * Pi / 20000;
double window_width;
main() {
int active = 1; // loop active
int trigger = 1; // first-time-through trigger
static char *p,
*q = city + CITYRL; // Ptr to byte after last byte
static int i;
static long fp; // file position pointer
static FILE *fh; // declare file handle pointer
static double mrofi, // Maximum range of interest =
*d, *r; // ½(width of map window)
double x, dlat, dlng; /* lat/long difference between
observer and observed */
MapInit(); // perform the map initialisation
trigger = 0; // set 'initialisation done'
/*Set up observer's name & co-ordinates in same format as the city data
is presented in disk file. Load them into elements [0] & [1] of the
coordinates array*/
p = "DESTINATION 53.28.100N 002:31.850W";
DstLat = DegRad(p + LATBYTE,0);
DstLng = DegRad(p + LNGBYTE,1);
p = "OBSERVER 51:52.000N 000:11.000E";
ObsLat = DegRad(p + LATBYTE,0);
ObsLng = DegRad(p + LNGBYTE,1);
/*This `leg' of the journey, ie the Destination Radial
on which vehicle must try to travel, is the bearing
of the origin from the destination's point of view: */
MaxRng = -1;
Radial = RandB(DstLat, DstLng, 1);
ObsVel = VEH_SPEED * KMH_RADS; // Observer's speed (radians/sec)
ObsHdg = 1.5; // Observer's heading (radians)
/*Set the maximum range at which a city is of interest. Root 2 times
(window_height) is the radius of the smallest circle within which the
square window will fit.*/
MaxRng = (mrofi = cos(1.414213562 * window_height));
/*Open the disk file containing the names & co-ordinates of the cities to be
displayed as reference points for the observer.*/
fh = fopen("WayPts.DAT", "r");
setvbuf(fh, NULL, _IOFBF, 4096); // allocate a 4k buffer to the file
/*Skip over the column titles at the beginning of the file and set the file
pointer to the start of the data for the first city.*/
fseek(fh, fp = CITYRL, SEEK_SET);
i = 0; // Set index to the first city in the list.
while(active) { // while scan OK and no key hit
if(kbhit()) active = 0; // if key struck, kill program
else {
/*Compute range & bearing of each city to be displayed in the map window */
if(i <= CITIES) { // If not all cities done
/*Advance to [next] city in list, get its Earth co-ordinates and
convert them from degrees and minutes to radians.*/
i++;
for(p = city; p <= q; p++) *p = getc(fh);
RefLat = DegRad(city + LATBYTE,0);
RefLng = DegRad(city + LNGBYTE,1);
/*Provided the centre of the map window is not at one of the poles,
make the East-West aperture of map window equal to its North-South
aperture (expressed in great-circle radians) times the cosine of
the latitude of the window's centre (ie of observer)*/
window_width = window_height;
if((x = cos(ObsLat)) > 0) window_width /= x;
/*Compute the latitude offset and longitude offset of the city from
the centre of the map window*/
dlat = fabs(RefLat - ObsLat);
if (dlat > Pi) dlat = TwoPi - dlat;
dlng = fabs(RefLng - ObsLng);
if (dlng > Pi) dlng = TwoPi - dlng;
/*Test if city is approximately within range of map window first by
seeing if its latitude offset is within window's vertical (north-
south) limits, if so, see if its longitude offset is within the map
window's horizontal (east-west) limits*/
if ((dlat <= window_height) && (dlng <= window_width )) {
/*If the city is known to be within the map window or at least close
to the map window's boundary, compute its range & bearing. If the
RandB() function found its range to be within 'maximum range of
interest' given in coords[4], then compute its screen x,y coordin-
ates and display the city's position and name in the map window*/
RandB(RefLat, RefLng, 0);
if(Range > 0) ShowNode(RBtoXY(SCALE), city);
}
}
//Display graticule and swap the display and active graphics pages etc.
else {
MaxRng = -1; // Disable range limit for RandB()
GndTrk(); // Advance observer's position
MaxRng = mrofi; // Reset Max Rng to window radius
ShowData();
fseek(fh, fp, SEEK_SET); // Re-initialise file pointer
i = 0; // Set to re-start display cycle
}
}
}
}
This function computes the distance & bearing of the point with latitude RefLat and longitude RefLng from the point with latitude ObsLat and longitude ObsLng. Range & bearing in radians is computed to approximately 52-bit precision in about 40 milliseconds on a PS/2 30-286.
Since in most cases, range & bearing are measured from the point of view of the observer, RandB() picks up the lat/long of the observer directly from the externals ObsLat, ObsLng. The lat/long of the point being observed is passed to RandB() by the calling function. The resulting range & bearing are placed in the externals Range and Bearing, and Bearing is also returned by the function. The 'Swap' switch when set to non-zero causes the Observer and the Observed to be interchanged so that the bearing of the Observer from the point of view of the Observed is returned.
#include <math.h>
#define Pi 3.1415926535 // Last modified 28 May 1991
extern double
ObsLat, ObsLng, // Lat/long of observer
MaxRng, // Cosine of max range of interest
Range, Bearing, // Computed range & bearing
CosRng, CosBrg; // Cosines of the range & bearing
double RandB(double RefLat, double RefLng, int Swap) {
double
temp, dlong,
SinObsLat, CosObsLat,
SinRefLat, CosRefLat,
SinRng;
if(Swap) {
temp = ObsLat; ObsLat = RefLat; RefLat = temp;
temp = ObsLng; ObsLng = RefLng; RefLng = temp;
}
dlong = RefLng - ObsLng, // Longitudinal difference
SinObsLat = sin(ObsLat), // Sine of latitude of observer
CosObsLat = cos(ObsLat), // Cosine latitude of observer
SinRefLat = sin(RefLat), // Sine of latitude of observed
CosRefLat = cos(RefLat), // Cosine latitude of observed
SinRng = 0;
Range = 0; Bearing = 0; // initialise externals
CosRng = 1; CosBrg = 1;
if(dlong > Pi) dlong -= Pi;
if(dlong < -Pi) dlong += Pi;
CosRng = CosObsLat * CosRefLat * cos(dlong)
+ SinObsLat * SinRefLat;
if(CosRng > +1) CosRng = +1;
if(CosRng < -1) CosRng = -1;
/*If computed range within specified maximum 'range of interest' to calling
function (expressed in MaxRng as cosine of maxi), then proceed with full
range and bearing computation, else leave range as zero and exit*/
if(CosRng > MaxRng) {
Range = acos(CosRng); // Compute the range in radians
/*COMPUTE THE BEARING
Evaluate bearing only if Sin(Range) is non-zero otherwise a division by
zero situation will arise in the following formula. If Sin(Range) is
exactly zero, then exit leaving Bearing as zero*/
if((SinRng = sin(Range)) > 0) {
//Standard spherical geometry formula for bearing.
CosBrg = (SinRefLat - SinObsLat * CosRng) / (CosObsLat * SinRng);
if(CosBrg >= 1) Bearing = 0; // Avoid possible acos domain errors
else // resulting from rounding errors in
if(CosBrg <= -1) Bearing = Pi; // evaluating the above formula.
else { // Else it's within acos domain (-1 to +1),
Bearing = acos(CosBrg); // so evaluate the actual bearing.
if(dlong < 0) // If longitudinal difference
Bearing = -Bearing; // is -ve, the bearing is -ve
}
}
}
if(Swap) { // Swap observer's and observed's lat/longs back if necessary
temp = ObsLat; ObsLat = RefLat; RefLat = temp;
temp = ObsLng; ObsLng = RefLng; RefLng = temp;
}
return(Bearing);
}
Latitudes must be expressed in range 90:00.000S to 90:00.000N. Longitudes must be expressed in range 180:00.000W to 179:59.999E. Returns a double length quantity in radians. Input is passed as a pointer to a string containing degrees, minutes and seconds of arc in the format "000:00:00X". Switch = 0 to pick up a latitude and 1 to pick up a longitude.
double DegRad(char *p, int Switch) {
int x, y; //Save first character of field
double c;
//Convert the whole degrees to integral Nº of minutes of arc
x = (*p++ - 48) * 10 + *p++ - 48;
if(Switch == 1)
x = x * 10 + *p++ - 48;
x *= 60; // degrees to minutes
p++; // jump over the colon
x += 10 * (*p++ - 48) + *p++ - 48; // + tens, units of mins
p++; // jump over decimal point
y = (*p++ - 48) * 100 // 100s of milliminutes
+ (*p++ - 48) * 10 // 10s of milliminutes
+ *p++ - 48; // single milliminutes
c = x;
c *= 1000;
c += y; // form total as a double
c *= 2.908882086574074E-7; // milliminutes to radians
x = *p; // Get N S E W letter
if ( x == 'W' || x == 'S' ) c = -c; // West & South are -ve
return(c);
}
Converts 'double' radians to a degrees, minutes, seconds display string:
char *RadDeg(double c) { // c = input in radians
long s; // long interger seconds
int h = 0, i, q; // int degrees, minutes, seconds
char *p = " ø ' "; // output string
if(c < 0) { // If angle is negative, then
q = '-'; // set up the minus sign
c = -c; // and make it positive.
} else q = '+'; // else set up the set minus sign
c *= 57.2957795141996; // convert radians to degrees
while(c > 100) { // find hundreds of degrees `h'
c -= 100; h++;
}
if(h == 0) *p = q;
else *p = h + 48;
for(i = 0; i < 3; i++) {
p++; // Skip over `hundreds' of colon
s = c; // interger of `c'
*p++ = s / 10 + 48; // Set tens
*p++ = s % 10 + 48; // Set units
c -= s; // chop integral part of 'c'
c *= 60; // multiply down to next unit
}
return (p -= 9); // return pointer to deg/min/sec
}
Please note that in the final implementation, trig frunctions are replaced by functions which use look-up and interpolation tables. These are designed to return values to an accuracy equal to the precision of the C-language's int type (normally 32 bits). And of course, they are considerably faster than the trig functions they replace.
Given the vehicle's current position, speed and heading this function updates the vehicle's position & heading based on the time that has elapsed since the last pass.
#include <sys\types.h> // getting System Time each pass
#include <sys\timeb.h> // Include library functions for
#include <math.h> // for sin, cos etc.
#define Pi 3.1415926535
#define TwoPi 6.283185307
#define RotMax 0.03 // Max rate-of-turn (radians/sec)
#define RotDmp 0.02 // Rate-of-turn damping factor
#define RotFac 0.03 /* Converts heading deviation in radians
to rate-of-turn in radians/second) */
extern double // gets range and bearing of destination
RandB(double Lat, double Lng, int Swap),
ObsLat, ObsLng, // Observer's (vehicle) lat/long
RefLat, RefLng, // Reference Object's lat/long
DstLat, DstLng, // Destination lat/long
ObsHdg, ObsVel, // Observer's heading and speed
ObsRot, // Observer's Rate of turn (radians/sec)
Bearing, // bearing of reference object
ReqHdg, // Heading Command
MaxRng, // Maximum range of interest
Radial; // Bearing of origin from destination
double BrgDif(double a, double b) { // BEARING SUBTRACTOR
double c = a - b;
while(c < -Pi) c += TwoPi;
while(c > Pi) c -= TwoPi;
return(c);
}
double RatAng(double a) { // EXPRESS AN ANGLE AS A VALUE
while(a < 0 ) a += TwoPi;
while(a > TwoPi) a -= TwoPi;
return(a);
}
GndTrk() { // UPDATE HEADING AND GROUND TRACK
static struct timeb T; // System time at last pass
static int ftt; // first-time-through flag
double HdgDot, // Hdg deviation/increment this pass
d, // Distance moved along track this pass
et, // Elapsed time (secs) since last pass
t, // double accommodation for T.millitm
lat, // Average latitude during move this pass
dlat; // Latitude component of vehicle
//COMPUTE THE ELAPSED TIME IN SECONDS SINCE THE LAST PASS
et = -(t = T.millitm) / 1000 - T.time;
ftime(&T); // Get system time now
et += (t = T.millitm) / 1000 + T.time;
/*If this is the first pass of the program since switch-on, simply put the
System Time in the 'T' time data structure to act as the reference from
which the elapsed time will be measured during the second pass. Then exit
without updating heading and ground track*/
if(ftt == 0) { ftt = 1; et = 0; }
else {
/*ELSE PROCEED WITH THE HEADING AND GROUND TRACK UPDATE
Compute required heading ReqHdg the vehicle must turn towards to bring
it smoothly on to the required radial of the destination waypoint*/
ReqHdg = RatAng(
RandB(DstLat, DstLng, 0) + // Bearing of destination from vehicle
RandB(DstLat, DstLng, 1) - // Bearing of vehicle from destination
Radial // Bearing of origin from destination
);
//Compute a rate of turn HdgDot proportional to current heading error:
HdgDot = RotFac * BrgDif(ReqHdg, ObsHdg);
//Impose a maximum limit to this rate of turn:
if(HdgDot > RotMax) HdgDot = RotMax;
else if(HdgDot < -RotMax) HdgDot = -RotMax;
//Apply damping to rate of change of observer's rate of turn:
ObsRot += RotDmp * et * (HdgDot - ObsRot);
//Update the observer's current heading:
ObsHdg = RatAng(ObsHdg += ObsRot * et);
//Compute distance moved along ground track since last program pass:
d = ObsVel * et;
/*RESOLVE DISTANCE MOVED INTO LAT & LONG INCREMENTS
Shift in latitude is simply distance along track times cos(heading).
Shift in longitude is distance along track x sin(heading) times the
cos(average latitude during the shift)*/
dlat = d * cos(ObsHdg); // change in latitude this pass
lat = ObsLat + dlat / 2; // average latitude during travel
ObsLat += dlat; // perform the latitude shift
/*SHIFT LONGITUDE BY RESOLVED WEST TO EAST MOVEMENT
The distance in full 'great-circle' radians moved in the West to East
Direction is d.sin(heading). But we need to express this in terms of the
(smaller) 'longitudinal radians' for the latitude concerned. This
(larger) figure is obtained by dividing d.sin(heading) by cos(lat),
where 'lat' is the average latitude of the vehicle while it is travel-
ling the distance 'd' during this pass of the program*/
ObsLng += d * sin(ObsHdg) / cos(lat);
}
}
Waypoint Encounter: the geometry involved in navigating an aircraft or ship towards an en-route way point, including the implementation of a demonstration applet.
Barges follow the course of the rivers and canals on which they float. These naturally lead them to their destinations. Trains are guided by the tracks on which they travel. Cars and trucks follow roads. All they have to do to reach their destinations is to take the right turn at each junction along the way. But ships at sea and aeroplanes have no permanent way to guide them. They rely on natural geographical features, lighthouses and other artificial navigational aids to guide them on their journeys.
For a ship, aeroplane or off-road vehicle a journey is made up of a sequence of way points. A way point is simply a point on the Earth's surface. It may be the location of a hill, mountain, lake, town or some other geographical feature. It may be the location of a lighthouse or radio navigation station. Or it may be simply a latitude and longitude recorded in the memory of a G.P.S. [global positioning system] receiver or a futuristic astral navigator which fixes positions using signals from pulsars.
The featureless separation between way points plays no part in guiding the traveller to his destination.
This project is concerned essentially with the navigation of aircraft. They are capable of flying over any part of the Earth's surface at high speed. This allows them to follow paths much closer to mathematical ideals than can other kinds of vehicle. There is a strong tendency to think the ideal path for an aircraft to follow to be a succession of hyperbolic encounters with its way points — a path rather like that of a small positively charged particle weaving between a sequence of large stationary particles which are also positively charged:
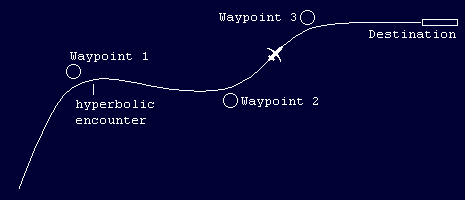
However, aircraft are not ideal particles or planets moving in free space: they are vehicles battling through a rather dense complex dynamical atmosphere. For them, therefore, the ideal — the most economical — path is not a series of hyperbolae, but one of straight lines joined by small circular arcs whose radii are equal to the radius of the aircraft's minimum comfortable turning circle.
The aircraft's route is set by the radial on which the aircraft must leave each way point. Consequently the aircraft must fly over the way point in the direction of the next way point en-route. To achieve this, we construct a circle passing through the way point we are approaching such that the tangent to the circle at the way point is the direction of the next way point.
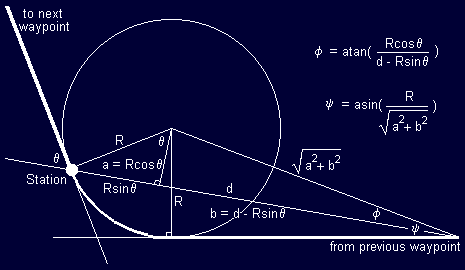
All angular computations are then performed relative to the centre of the constructed circle. The aircraft never passes near the centre of the circle. Nasty infinities therefore can never occur to cause trigonometrical confusion. If the aircraft drifts off course, a new circle is constructed, thus maintaining the integrity of the trigonometry.
As computer software, this could form the basis of an automatic flight control system of the future. Integrated with international flight plan processing, it could form the basis of a completely automated system of global air highways.
I have designed, programmed and exhaustively tested a software kernel to provide this navigational functionality. I have coded part of it in Java and installed it herewith as a demonstration applet to give some idea of my capabilities in this area. However, please be aware that a vast amount of applied expertise is needed (hopefully some of mine) to transform the core functions demonstrated in the applet into a safe automatic flight control system.
The spherical range and bearing computations described in this document's parent use the universally familiar sin and cos functions quite liberally. Many people see these pure mathematical functions as quite beautiful. They see them as a reflection of nature. Or even as part of the very fabric of the universe. This is undoubtedly because, when viewed against a fixed frame of reference in space and time, they trace out apparently smooth (and beautiful) periodic curves. The idea of replacing such things of beauty with something as crude and frumpy as a look-up table is considerd to be pure anathema.
This beauty is however like all beauty: in the eye of the beholder. Nature does not set out to make sine curves. They are merely one consequence of one microscopic event following another ad infinitum. They are the global outcome of a myriad iterations of a single fractal process. They become visible to us only when we take our observer's licence of freezing time and rigidifying space with our artificial systems of co-ordinates and units of measurement. They are nothing more than human aids to comprehension.
The lowly look-up table, on the other hand, makes no pretence of being the fabric of the universe. Nevertheless, it does define the same set of waypoints which the natural fractal process visits on its journey through time and space. And it finds them for you much more quickly than does the 'pure' mathematical function. The truth is that neither one is a fundamental component of the universe. Reality is relativistic and fractal. You cannot freeze time or rigidify space. Motion is key to existence.
The mathematician and the physicist with their beautiful functions therefore have no cause to look down upon the engineer and the programmer for using look-up tables.
© 1997 Robert John Morton




