O meu interesse em:
Teoria do Caos
Introdução
Equação Diferença
Mapas de Bifurcação
Conjunto de Mandelbrot
Atraídor de Hénon
Função Iterativa
Imagens de Lissajous
Programa: chaos.c
[Para executar este programa, por favor consulte o final do documento.]
[English Version]
Um dos meus programas relacionados ao caos é este applet Java que escrevi para exercitar duas equações de diferença x = cx (1 − x) e x = x² + c. Ele demonstra como a simples alteração do valor da constante c altera todo o comportamento da equação. O applet ilustra um processo matemático que se pensa ser a chave para a próxima fase da busca do homem para entender a natureza. Este mesmo processo também é entendido como a força motriz das economias nacionais - e, de fato, a economia global como um todo. Por conseguinte, é de importância crítica para aqueles que procuram estabelecer políticas econômicas e sociais para o futuro.
Você deve encontrar este applet fácil de operar e adequado para o propósito dele. No entanto, se você estiver interessado em explorar o comportamento dessas e outras equações, você pode modificar e recompilar o código fonte fornecido, mas, depois de ter feito, você é educadamente solicitado a reconhecer o meu trabalho como o autor desta versão original do applet.
Se, com o Microsoft Windows, aparece uma caixa de segurança dizendo que o aplicativo foi bloqueado porque não é confiável, clique aqui. Se você receber mensagens de aviso com o Linux, clique aqui.
Isto inclui o cálculo do valor de y de uma equação não-linear y = f (x), traçando-o, depois para realimentar y novamente na equação como x e para repetir o processo sem parar. É o que é conhecido como um ciclo de realimentar positivamente. Exemplos práticos são: o processo de vida e os processos de fornecimento e demanda em um mercado livre.
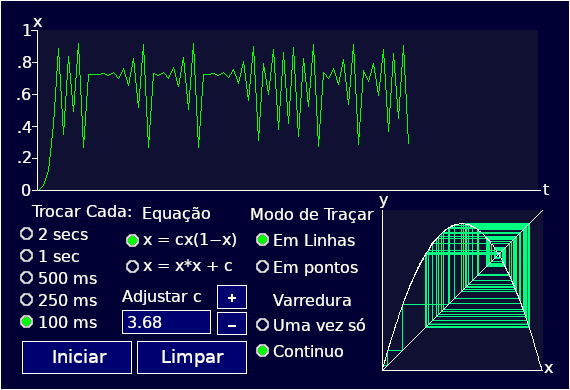
O applet torna visível este processo de iteração através do gráfico de Rebote mostrado no canto inferior direito da área de exibição. O applet traça a curva de y = f (x) e a linha diagonal reta y = x. O processo de iteração começa a partir do ponto na diagonal correspondente ao valor inicial de x. Em seguida, traça uma linha a partir deste ponto verticalmente para atingir a curva y = f (x). Isto produz o valor correspondente de y. A partir deste ponto, ele projeta uma linha horizontalmente até atingir a diagonal. Isto efetivamente alimenta este valor de y na equação como x para a próxima iteração. Arrumado! Ele traça as linhas de retorno da iteração atual em verde escuro e, em seguida, re-traça as linhas de retorno da iteração anterior em verde claro. Se você diminuir a taxa de iteração para baixo para plotar a cada 2 segundos você verá claramente este processo funcionar. O applet traça um gráfico de Tempo (de x versus tempo) em simultâneo com o seu gráfico de Rebote.
À medida que as iterações se montam no gráfico de rebote, as linhas verdes brilhantes acumulam-se em um atrator no espaço-de-fase bidimensional formado por plotar xn versus xn-1. Para os valores de c que produzem comportamento linear e periódico, o atrator é simplesmente um ponto ou um quadrado. Se as variáveis x e t fossem contínuas em vez de discretas, os quadrados seriam círculos ou elipses como produzidos pelo meu applet das Figuras de Lissajou.
Quando o comportamento torna-se caótico, o atrator torna-se "estranho" - uma sucessão de retângulos em mudança. Dentro da precisão do raster de pixeis da tela, alguns retângulos parecem repetir e sobreporem-se. Porem, dentro da dupla-precisão da aritmética de ponto flutuante IEEE usada no programa, eles nunca sobreporem-se exatamente. Novamente, se as variáveis x e t fossem contínuas em vez de discretas, o traço assemelharia-se a algo parecido com a máscara de coruja ou o traço de borboleta que se tornou conhecido como o atrator estranho de Lorenz.
Surpreendentemente, o tipo particular da função f usada parecer não afetar o comportamento fundamental do processo de iteração. Não precisa ser nenhuma das duas funções incorporadas pelas equações escolhidas para o applet. Outras funções exibem o mesmo tipo de comportamento, desde que sejam não-lineares (ou seja, elas produzem curvas e não linhas retas). Tudo o que a mudança da função parece fazer é reposicionar, redimensionar e remodelar tão ligeiramente o caminho traçado por valores sucessivos de x em relação à origem do sistema de coordenadas no qual eles são plotados.
Seja qual for a função particular usada para a equação de diferença, ela exibe um dos três tipos de comportamento de acordo com o valor atual da constante c, a saber:
Para c < 2,1, a iteração desta equação produz a curva sigmoide familiar usada para representar o crescimento de plantas e árvores, populações, demanda do mercado e uma infinidade de outras coisas. Para 2,1 < c < 2,9, a curva sobe ao máximo, depois segue uma oscilação moribunda que eventualmente se ajusta a um valor constante. Para 2,9 < c < 3,4 a curva sobe como de costume, mas estabelece-se em uma oscilação regular. Para 3,4 < c < 3,6, a oscilação torna-se cada vez mais complexa, em um ponto adotando um tipo de ritmo de valsa. De 3,7 < c < 4 oscilações regulares dão lugar ao comportamento caótico. Para c < 4, isto torna-se tão extremo que a "população" logo faz um mergulho caótico para zero, do qual não pode se recuperar - como se uma população se extingue.
Isto é matematicamente equivalente à outra equação acima, de modo que seu comportamento será o mesmo, e também pode representar os processos naturais representados pelo outro.
Esta equação pode ser considerada como uma versão de "eixo real só" da equação de diferença complexa z = z² + c que gera o Conjunto de Mandelbrot.
Ambas as equações são funções parabólicas. Quando plotados, eles produzem parábolas. As diferenças entre as equações não estão relacionadas com a natureza do que descrevem. É apenas fazer com a posição a partir da qual o que eles descrevem é observado. Alterar a posição eo ângulo a partir do qual você observa uma coisa não altera a própria coisa.
A essência de uma parábola é descrita completamente pela equação y = x². Todos os outros termos na forma geral da equação de uma parábola são simplesmente fazer com a partir de onde o observador escolhe observar-a. Ou seja, onde ele escolheu colocar o centro do seu quadro de referência, e o grau de ampliação que ele usará enquanto medir o que ele observa. O observador, por definição, reside sempre na origem (ponto 0, 0) do seu sistema de coordenadas
A forma geral da equação para uma parábola é ax² + bx + c onde:
'a' é o fator de ampliação que determina o tamanho ou a escala da parábola em relação à unidade de medida do observador,
mudar 'b' move a origem coordenada (e, portanto, o observador) em torno da curva atual da parábola,
'c' é o fator de mudança vertical que determina o quão alto ou para baixo a parábola é deslocada em relação ao observador.
Os efeitos dessas 3 variáveis são sobreposto uma na outra. Por exemplo, quando c não é zero, uma mudança em b move o ponto y = c (não a origem coordenada y = 0) em torno da curva da parábola. O ponto essencial de tudo isto é que uma parábola é sempre uma parábola, ou seja, y = x². Toda a outra parafernália, na forma generalizada da equação, é simplesmente para fazer com onde o observador está. E onde o observador está não pode afetar a natureza intrínseca e o comportamento do que é observado. Então, para estudar o comportamento da equação, não importa qual equação específica está usada, enquanto for uma parábola.
Todas as formas da equação podem ser mapeadas umas nas outras simplesmente por alterar a posição do observador. Para mudar de ver uma parábola como y = cx(1 − x) para vê-lo como y = x² + c, faça o seguinte:
Mova metade de uma unidade à sua direita. A equação é agora y = c(½ + x)(½ − x) que simplifica para y = c(¼ − x²)
Vá ao redor das costas e vire-se de cabeça para baixo. A equação é agora y = c(x² − ¼)
Coloque um par de óculos astigmáticos que reduzam a escala y por um fator de c. A equação é agora y = x² − ¼c. Então deixe a constante c na nova equação ser o que ¼c estava no antigo. Assim, a equação torna-se y = x² + c.
No entanto, o que você está olhando não é alterado. O motivo para mudar a sua posição de observação é que a segunda equação é mais simples e, portanto, mais fácil de construir em um programa de computador e mais rápido para calcular. Em programas iterativos, o tempo é essencial.
Os cientistas costumam curvar, dobrar, escalar e torcer representações gráficas de fenômenos para torná-los mais visíveis. O atrator estranho de Hénon é um exemplo excelente. A dificuldade é que eles não podem mais ser capazes de correlacionar facilmente a nova forma de suas equações com o fenômeno do mundo real que estão tentando simular e do qual eles derivaram as suas equações originais. É tudo uma questão de compromisso - e um aspecto muito interessante da relatividade.
A primeira equação do applet x = cx (1 − x) é conhecida como Equação de Diferença Logística Padrão. Ela modela, entre outras coisas, a forma como as populações, de formas de vida reprodutiva, aumentam-se e diminuem-se. Neste contexto, a constante c representa a fecundidade da forma de vida em causa, ou seja, a ferocidade com a qual ela se reproduz. Isto é moderado por um fator que representa o grau de facilidade ou dificuldade com que a espécie é capaz de adquirir as suas necessidades da vida a partir do meio ambiente. A população é assim mantida em equilíbrio por um mecanismo análogo a um amplificador com retroalimentação negativa, ou um motor com um regulador de velocidade sensível ao torque, ou uma economia de mercado regulada pelas taxas de juros.
As populações humanas e animais seguem uma curva sigmoide suave como a produzida pelo applet para c < 2,1 na equação x = cx (1 − x). Tente c = 1,85 para um bom exemplo de uma população sigmóide. Atualmente, a população mundial humana é pensada para cerca de 0,4 na escala vertical do gráfico do tempo. O que corresponde a cerca de 6.000 milhões. Mas isto não significa que a Terra não pode suportar mais de 6750 milhões (0,45 no gráfico, o ponto em que ele níveis fora). Significa simplesmente que não pode fazê-lo sob o atual nível de tecnologia e sob o regime socioeconômico atualmente dominante.
Em sistemas dinâmicos complexos, especialmente, há um atraso entre causa e efeito. Para a população humana, esse atraso é muito curto em comparação com o ciclo de reprodução. É por isso que a curva que a população humana segue é um sigmoide suave. Mas com insetos, devido à sua alta fecundidade, o atraso é significativo. Os efeitos das mudanças ficam atrasados de suas causas. Isto causa algumas populações de insetos aumentar e diminuir chaoticamente, correspondendo ao comportamento da equação para c = 3,6 ou por aí. Isto tem um significado para o futuro da humanidade de uma maneira que é mais imediata e menos óbvia do que se supõe.
A primeira equação do applet x = cx (1 − x) é conhecida como Equação de Diferença Logística Padrão. Ela modela, entre outras coisas, a forma como a população de um produto cresce dentro de seu potencial mercado. Neste contexto, a constante c é uma amálgama de dois fatores. O primeiro representa a produtividade - o número de unidades de produto que podem ser fabricadas por uma unidade de esforço humano. Isso é ampliado pela tecnologia de produção. O segundo representa o número de unidades de produtos que podem ser vendidas no mercado por uma unidade de esforço humano. Isto é ampliado pela tecnologia de comunicação. No entanto, é diminuído pela concorrência. A população de um produto dentro de um mercado é assim mantida em equilíbrio por um mecanismo semelhante ao que mantém as populações da vida em equilíbrio com seus ambientes.
A natureza fornece generosamente as necessidades da vida em troca do trabalho humano. Na ausência de guerra, opressão e exploração, todos poderiam viver no conforto e no bem-estar. O valor de c fornecido pela natureza (suponha que seja cerca de 1,3 ou 1,4) é mais do que adequado para as necessidades da humanidade. Ele cria uma economia com uma curva de produtividade suave. Mas a forma de vida humana começou então a desenvolver tecnologia. Primeiras ferramentas, em seguida, a roda, depois máquinas, depois automação, computadores, comunicações e mídias de massa.
O sigmoide suave atingiu alturas cada vez maiores. Uma vez que c passou 2,34, a curva começou a badalar quando atingiu o topo. Ou seja, produção ultrapassou e depois caiu de volta à sua taxa estável. A amplitude de badalar cresceu cada vez mais até, quando c = 2,9. Neste ponto começou exibir um ritmo quase constante (embora superficial) de boom e busto. Isto foi quando as economias ocidentais gradualmente emergiram a partir do final da Segunda Guerra Mundial. No entanto, conforme mostra o gráfico de tempo do applet, a relação entre boom e busto gradualmente desapareceu. Acha que isto prova que a política econômica do governo está funcionando? Penso que não.
No qualquer jeito, a tecnologia continua avançando, gerando maior produtividade e aumentando mais o poder e alcançamento de marketing.
O resultado é que a relação entre boom e busto fica maior, mas agora não desaparece. À medida que c aumenta mais, também a relação entre o boom e o busto, até o seu ritmo torna-se mais complexa. Provavelmente vamos deixar o século 20 com muitas economias nacionais crescendo e rebentando de acordo com este hipnotizante "ritmo de valsa". Mas o que do futuro? O que o novo milênio mantém para as economias nacionais? Em uma palavra: caos. O progresso técnico não vai parar. Pelo contrário, a sua taxa de progresso acelerará. O ciclo do boom-busto provavelmente logo vai seguir o perfil de c = 3.68 que foi estava sendo traçado pelo applet quando você o viu pela primeira vez.
É improvável que os ciclos econômicos caóticos prejudiquem as economias nacionais ou aqueles que as controlam. No entanto, eles vão arruinar e destruir a vidas econômicas das pessoas comuns. Ou seja, a menos que as regras de engajamento entre o indivíduo e o corpo corporativo sejam substancialmente reestruturadas.
O painel de controle do applet é a coleção de botões, etc. no quarto inferior esquerdo da janela do applet.
O applet de demonstração de iterações da equação de diferença é composto das seguintes classes:
Muito antes de ser melhorado e reescrito em Java, este demonstrador de iterações de equações de diferença iniciou a vida como três programas separados escritos no MS QuickBASIC 2.0 (que mostra quanto tempo atrás isso foi!). Para os arqueólogos de software entre vocês, estes três programas originais: stdLog.bas, stdLog1.bas e stdLog2.bas devem revelar-se artefactos muito interessantes. No entanto, eles oferecem uma apresentação um pouco diferente do que o do applet.
Você precisa do Java instalado em seu computador. Então:
Nota: não obstante os avisos "oficiais", este programa não vão explodir o seu computador nem causar qualquer outro tipo de dano fantasioso. Ele simplesmente desenha gráficos na tela. Nos bons e velhos tempos, este programa simplesmente era executado dentro da página da web, onde sua imagem estática é exibida agora. O applet incorporado ainda é executavel em versões anteriores a 2017 dos navegadores com o Java 1.6 instalado e a versão do Web Start ainda é executavel nas versões anteriores a 2019 dos navegadores com o Java 1.8 instalado. Para ler a história rançosa deste triste retrocesso na funcionalidade da Web, clique aqui.
[Back to top.]
Você também pode experimentar com uma versão deste programa escrita em 'C'. Observe que os controles na versão 'C' são um pouco diferentes, mas sua operação é, no entanto, essencialmente evidente. [De volta ao topo.]