Teoria de Caos: Applets das Mapas de Bifurcação

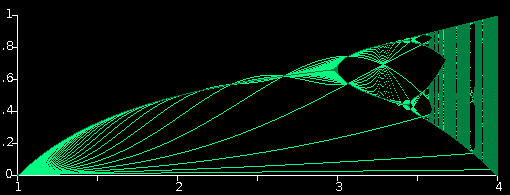
Em seu modo de traçado de "valor pontual", o Applet de Equação de Diferença traça os valores de ponto de x para as primeiras 70 iterações ao longo do gráfico de tempo. Quando o fim do eixo do tempo está alcançado, ele volta para a es­querda e continua a traçar x através do eixo do tempo repetidas vezes. No entanto, lá, você só pode ver o envelope para o valor de c usado no momento, ou seja, o mostrado no campo 'ajustar c'.

O applet acima, por outro lado, traça laboriosamente os envelopes dentro dos quais x vagueia por uma ampla gama de valores de c. Aqui, no entanto, os envelopes são cada um pixel de largura em vez de 6. Este applet traça os envelopes para a Equação de Diferença Padrão de Logística:

x = cx(1 − x) para c = 1 a 4.

Para c < 1, x não pode sair do chão. Isto é análogo à circunstância impossível de uma espécie que parte de uma população inicial de zero ou 1. Para c > 4, x salta tão caoticamente que ele logo atinge zero do qual nunca pode recuperar-se. Esta situação é análoga ao desaparecimento catastrófico de uma espécie devido a uma fecundidade excessiva e à resultante inadequação do seu abastecimento alimentar.

O atractor de x para cada valor de c é plotado em verde escuro. A aura verde bril­hante indica o número de iterações necessárias para que x atinja o atractor a partir do seu valor inicial. Pode ser pensado como o inverso da força atrativa (ou "gravi­dade") do atractor.

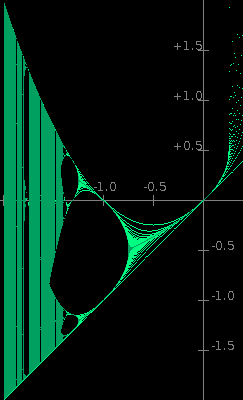O applet na esquerda traça um mapa equival­ente dos envelopes para a equação de diferença x = x² + c. Esta é uma versão apenas de eixo real da equação z = z² + c usada para gerar o Conjunto de Mandelbrot. O Conjunto de Mandel­brot ficaria no plano horizontal perpendicular à tela (provavelmente paralelo ao plano da mesa no que o seu computador está localizado). A jun­ção entre o corpo principal do "besouro preto" do Conjunto de Mandelbrot e sua cabeça fica no eixo c, em linha com a primeira divisão no atrator (aproximadamente onde c = −0,75). A cabeça do "besouro preto" termina e seu nariz começa no ponto do eixo c, onde o atrator divide-se em 4 (aproximadamente onde c = −1,2). O objeto 3D, que mapearia a equação complexa z = z² + c (do qual o Conjunto de Mandelbrot seria sua projeção no plano com­plexo onde x = 0) seria uma aparição mate­mática muito intrigante. Eu originalmente escr­evi esses programas em C.

NOTA: Se, com o Microsoft Windows, aparece uma caixa de segurança dizendo que o aplicativo foi bloqueado porque não é confiável, clique aqui. Se você receber mensagens de aviso com o Linux, clique aqui.

---

© novembro 1997 Robert John Morton | ANTE | PROX