Robert John Morton
About my interest in:
Chaos Theory
Introduction
Difference Equation
Bifurcation Maps
Mandelbrot Set
Hénon's Attractor
Iterative Function
Lissajous Figures
Program: chaos.c
Clique na bandeira
para ler em Português.
Robert John Morton
About my interest in:
Introduction
Difference Equation
Bifurcation Maps
Mandelbrot Set
Hénon's Attractor
Iterative Function
Lissajous Figures
Program: chaos.c
Clique na bandeira
para ler em Português.
Having read about the Mandelbrot Set, I simply had to write an applet myself to generate it. It must be one of thousands. It is probably not the best. [Português]
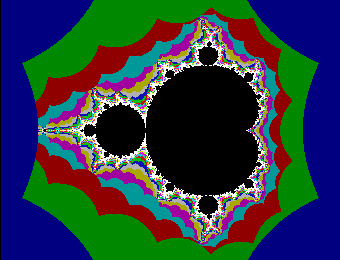But for me this was not the point. The point for me was seeing this complex image materialise from such simple code. My fascination came from my realising that this complexity was born not out of an obscure incomprehensible form of mathematics or fancy programming but was the result of a simple iterative process which exhibited an amazing phenomena that is woven, by nature, into the fundamental fabric of numbers.
In this applet the x-axis runs from −2·2 to +1·2 and the y-axis runs from −1·3i to +1·3i. You can extend the coverage by altering the constants XMAX, YMAX, XBIAS and YBIAS in the Java source code and then recompiling it. You can explore different parts of the Mandelbrot set at different scales of magnification by suitably altering these same constants.
I first prototyped my Mandelbrot Set generator in QuickBASIC. I then developed it further in C before Java materialized as the language of the Web.
If with Microsoft Windows a Security box pops up saying that the application has been blocked because it's untrusted please click here. If you get warning messages with Linux, please click here.